Уравнения Максвелла

Следующее краткое замечание касается уравнений Максвелла (современной, общепринятой их формы). Напомним, что они получены феноменологическим обобщением опытных фактов при малых скоростях (взята аналогия с гидродинамикой). Следовательно не стоит ожидать, что они угаданы в окончательной форме. Уравнения Максвелла (или волновое уравнение) определяют фазовую скорость, в то время как у теории относительности есть "претензия" на максимальную скорость сигналов (групповую скорость). Фактически, мы всегда имеем дело с конкретным светом, поэтому этот факт должен быть отмечен некоторым индексом: вместо $c$ нужно писать параметрическую зависимость $c(\omega)$ и волновое уравнение будет уравнением для Фурье-гармоники. Поскольку современные апологеты релятивизма отказываются от наглядности и принципиальной необходимости моделей среды распространения света, то неоднозначным становится путь обобщения уравнений Максвелла даже для "абсолютной пустоты" в случае немонохроматического света, не говоря уже о переходе к реальным нелинейным средам (включающим свойства "межмолекулярной пустоты", механизмы поглощения и переизлучения света молекулами и т.д.): без физических принципов, чисто из математических соображений таких обобщений можно ввести сколько угодно и все они будут равноправны. Требование инвариантности уравнений Максвелла относительно преобразований координат и времени весьма зыбкое, так как поля и уравнения для них можно ввести множеством способов, лишь бы измеряемые воздействия этих полей соответствовали реально наблюдаемым в экспериментах величинам. Так, например, в [81] показано, что существуют нелокальные преобразования полей, сохраняющие уравнения Максвелла с неизменным временем. В [14] показано, что можно ввести нелинейные и нелокальные преобразования, чтобы при определенных трансформациях полей уравнения поля были инвариантны относительно преобразований Галилея.

Продемонстрируем методическое противоречие общепринятых преобразований для полей. Пусть имеются два бесконечных незаряженных параллельных провода. Пусть в обоих проводах электроны движутся в одном направлении с постоянной скоростью относительно положительно заряженного остова, то есть имеем одинаковые плотности токов ${\bf j}$. Тогда для классического случая в выражении для поля величина

$$jdV = en(v_{+} - v_{-})dV$$

является инвариантом, то есть поле $H_{\perp}$ и воздействие этого поля не зависит от скорости движения системы. Для релятивистского же рассмотрения (так как ${\bf E} = 0$) имеем

$$H_{\perp} = {H_{\perp}^0\over \sqrt{1-v^2/c^2}},$$

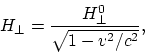
то есть поле зависит от скорости движения наблюдателя. Однако, следующие два случая очевидно равноправны:
(1) система со скоростью ${\bf v}_{obs} = 0$, то есть наблюдатель покоится относительно остова, а электроны движутся со скоростью ${\bf v}$, и
(2) система движется со скоростью ${\bf v}_{obs} = {\bf v}$, то есть наблюдатель покоится относительно электронов, а остов (положительные ионы) движется в противоположном направлении со скоростью $-{\bf v}$ (тот же самый ток). Релятивистская же формула дает для этих случаев разные значения $H_{\perp}$ (и воздействий полей), что абсурдно. Кроме того, совершенно противоречивым оказывается описание в СТО переходов от одной инерциальной системы к другой для трехмерной ситуации с ненейтральными токами (например, с пучками заряженных частиц).

Разберем теперь "принципиальный" вопрос об инвариантности уравнений Максвелла, широко разрекламированный в СТО. Инвариантность уравнений Максвелла относительно преобразований Лоренца совершенно ничего не означает для других явлений. Во-первых, уравнения Максвелла - это уравнения для полей в пустом пространстве. В таком пространстве мы можем отрезать половину отрезка и увеличить ее вдвое - получим такой же отрезок. Поэтому в пустом математическом пространстве можно пользоваться любыми системами отсчета, непротиворечивыми геометриями и переводными коэффициентами. Это может определяться только лишь удобством математического описания. Однако, мы не можем просто разрезать живой организм и увеличить его вдвое под микроскопом - организм умрет. Наличие в пространстве реальных физических тел и полей задает естественные реперные точки, характерные масштабы и взаимосвязи между объектами. Все это определяет отличия реального физического пространства от пустого математического пространства. Во-вторых, свойство некоторых взаимодействий распространяться в вакууме со скоростью света не детерминирует скорость распространения взаимодействий в среде. Несмотря на огромную роль электромагнитных взаимодействий, возмущения в средах распространяются со скоростью звука. По одной константе $c$, относящейся к вакууму, невозможно определить (для нашего "электромагнитного" мира) скорости звука и света в газах, жидкостях и твердых телах. Не ясно, как в изотропном пространстве могла бы возникнуть анизотропия реальных твердых тел. Все эти и многие другие свойства выходят за пределы применимости уравнений Максвелла в пустоте (СТО же предлагает клонирование свойств пустоты на все свойства материальных тел и сред). Следовательно, подгонять свойства всего мира под инвариантность уравнений Максвелла в пустоте - слишком завышенная претензия СТО. В-третьих, разбиение единого по своему действию поля на электрическую и магнитную части довольно условно и в значительной мере произвольно. Поэтому инвариантность этих искусственно выделенных частей не может иметь решающего значения. Наличие коэффициентов $\rho,\epsilon,\mu$ (зависящих от координат, времени, свойств света и др.) для уравнений Максвелла в среде делает эти уравнения неинвариантными относительно преобразований Лоренца (или опять нужно отменять объективность характеристик среды).