Дополнительные замечания

В классической физике все понятия имеют четко определенный смысл и не надо их подменять суррогатами. Пусть релятивисты выдумывают своим новым понятиям (вернее сочетаниям символов) иные названия. Релятивистское определение координат центра инерции [17]:

$${\bf R} = {\sum E{\bf r}\over\sum E}$$

не имеет физического смысла, так как в СТО центр инерции одной и той же системы движущихся частиц оказывается различен в разных системах отсчета. Значит он не выполняет своего функционального назначения центра равновесия. Пусть мы имеем массивный плоский ящик, в котором движутся массивные шарики. Пусть в классическом случае центр инерции всей системы в процессе движения и столкновения шаров всегда совпадает с центром ящика. Тогда в классическом случае мы можем его уравновесить (например, в поле тяжести Земли или ином поле) на опоре малого сечения (Рис. 4.3) и равновесие будет сохраняться.

Рисунок 4.3: Центр инерции системы и равновесие.

В СТО, напротив, если мы только посмотрим на эту систему из быстро движущейся релятивистской ракеты, то центр инерции может оказаться не над опорой и равновесие будет нарушено. Замечательная объективность СТО: чтобы не нарушать равновесие плазмы в управляемом термоядерном синтезе, просьба релятивистским ракетам не летать и не подглядывать за экспериментом.

Релятивистская связь массы и энергии на самом деле ничего принципиального не отражает. Действительно, классическое выражение кинетической энергии

$$E = {mv^2\over 2}$$

и релятивистское выражение

$$E=mc^2\biggl ( {1\over \sqrt{1-v^2/c^2}} - 1\biggr )$$

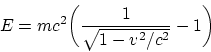
ничем существенным (качественно) не отличаются. Обе эти величины являются расчетными величинами. Попытка измерить эти величины (то есть градуировка прибора) зависит от интерпретации теории, так как эти величины не могут определяться из сравнения с эталоном. Поскольку в релятивистское выражение энергии

$$E = {mc^2\over \sqrt{1-v^2/c^2}}$$

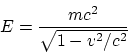
кроме массы входят и другие величины, то при любых возможных взаимосвязях масса и энергия останутся разными (неэквивалентными, независимыми) величинами. Даже для так называемой "энергии покоя" $E=mc^2$ не может идти речь о взаимных превращениях массы и энергии. Дело в том, что при аннигиляции (единственный кандидат на подобный процесс) образуются фотоны, для которых "масса движения" постулируется в СТО по той же самой формуле. Следовательно, и в этом случае речь идет просто о взаимных превращениях частиц. Не говоря уже о том, что "энергия покоя" - это только гипотеза СТО, так как теория приводит все к той же неопределенной константе, как и в классической физике.

Обратим внимание также на неинвариантность формулы $E=mc^2$ в рамках СТО: масса инвариантна, скорость света - тоже. Однако энергия представляет собой 4-вектор. Если попытаться включить в энергию тела кинетическую энергию его молекул, двигающихся с разными скоростями ${\bf v}_i$, то при переходе в движущуюся систему эти скорости будут по-разному складываться со скоростью тела как целого. В результате взаимосвязь оказывается нарушенной и в новой системе эта формула оказывается просто релятивистским определением некоторой "буквы $E$".

СТО пытается с принципиальных позиций "воевать с ветряными мельницами": например, с понятием абсолютно твердого тела. Однако, в классической физике никто не вкладывает буквального смысла в абстракцию абсолютно твердого тела. Всем очевидно, что абсолютно твердых тел не бывает даже при совсем нерелятивистских скоростях (отметим роль ускорений, точнее сил, в этом вопросе, вспомнив обычные столкновения машин на дорогах). Просто при описании некоторых движений влияние деформаций пренебрежимо мало или несущественно для изучаемого явления и тогда, только для упрощения математических выкладок, используется абстракция абсолютно твердого тела. СТО пытается принципиально считать элементарные частицы точечными [17] и сразу же сталкивается с другой принципиальной проблемой - сингулярностью ряда величин.

Перейдем теперь непосредственно к замечаниям по релятивистской динамике (теории столкновений и законам движения заряженных частиц).