Энергия и импульс в СТО

Начнем с замечания по поводу единиц измерения. Выражение импульса и энергии в единицах массы не может дать ничего полезного, так как эти величины невзаимозаменяемы, число совместных операций с ними (и комбинаций) ограничено и все равно за ними приходится следить как за разными физическими величинами. Стоит ли вносить путаницу в достаточно хорошо согласованные единицы размерностей?

Является ли единственным подход СТО к релятивистской динамике? Вовсе нет! В классической физике разделение энергии на кинетическую и потенциальную может быть довольно условным. Например, в статистической физике при описании движения в неинерциальных вращающихся системах к потенциальной энергии фактически относят среднюю кинетическую (!) энергию движения системы: из $v_{\varphi}=\Omega\rho$ образована $E_{пот}=m\Omega^2\rho^2/2$. Существует другой поучительный пример из гидродинамики, когда вводится понятие присоединенной ("эффективной") массы для описания движения тела сквозь среду. Ясно, что настоящая масса не изменилась в этом случае. Точно также и в релятивистской механике новая "скоростная" добавка к ускорению может быть связана с потенциальной энергией тела, а кинетическую энергию тела можно оставить неизменной и рассматривать классические уравнения Ньютона, но с другой "эффективной" силой и постоянной массой $m_0$.

Вопреки утверждениям СТО о важности и необходимости введения 4-векторов, даже для трех взаимодействующих частиц выражения

$$E = \sum_i m^{(i)}c^2\gamma^{(i)}, ~ ~ ~ ~ {\bf P} = \sum_i m^{(i)}{\bf v}^{(i)}\gamma^{(i)},$$

где

$$\gamma^{(i)} = {1\over \sqrt{1-v_i^2/c^2}}$$

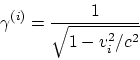
не составляют 4-вектора и не сохраняются. Сложности вызывает и введение потенциальной энергии взаимодействия частиц. Неужели СТО - это теория двух тел? Где же заявляемая всеобщность (универсальность)? Аналогичные сложности возникают при построении функций Лагранжа и Гамильтона для систем взаимодействующих частиц.

Предельный переход к классической энергии тоже противоречив. Выше говорилось об условии такого перехода $c\rightarrow\infty$. Но тогда не только энергия покоя, но и любая энергия будет $E=\infty$ в СТО. Не является последовательной и запись релятивистского импульса в форме [26] ${\bf P}=m(d{\bf r}/d\tau)$, так как $d{\bf r}$ относится к неподвижной системе отсчета, а $d\tau$ (собственное время) относится к движущейся системе (телу).

Предельный переход к малым скоростям для многих величин порождает ряд вопросов. Все формулы должны переходить к Ньютонову виду, когда скорость передачи взаимодействий предполагается бесконечной (например, функция Лагранжа, действие, энергия, функция Гамильтона и др.). Однако, мы видим [17], что это не так: 4-скорость переходит в набор четырех чисел (1,0,0,0) и ничего не означает, 4-ускорение - тоже; интервал $S\rightarrow\infty$ и величина $dS$ зависит от порядка предельного перехода; стремятся к нулевому набору компоненты 4-силы и т.д.. Это наглядно показывает, что все упомянутые релятивистские величины и выражения не могут иметь самостоятельного физического смысла.