Le temps unique absolu

La notion du temps est plus large, que le coefficient dimensionnel de la proportionnalité dans les lois de la transformation, et a plus à voir avec l’irréversibilité locale des processus. Premièrement la liaison sûre du temps avec le mouvemet d’un objet ne tient compte des processus qui peuvent ne pas être isotopiques, passer avec de "vitesses" différentes et caractériser l’irréversibilité locale (chacune de ses "vitesses" additionne géométriquement de la manière différente avec la vitesse d’un corps comme de l’entier). Deuxièmement, la liaison du temps uniquement avec la vitesse de la transmission des interactions électromagnétiques ne tient compte des autres interactions possibles (qui peuvent se propager dans le vide) et en fait signifie la nature électromagnétique de tous les phénomènes (l’absolutisation des interactions électromagnétiques). De ce, comment on peut introduire le temps unique absolu, on va parler au-dessous.

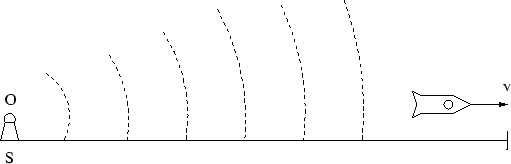
Quand on introduit la notion du temps propre (en fait, du temps subjectif) il y a un point méthodique qui semble être important. Il ne faut pas calculer le temps d'un autre objet (selon nos propres régles), mais en le "demander". Examinons l’expérience suivante (Figure 1.8).

Figure 1.8: L’échange de signals de temps propre.

Supposons qu’un observateur se trouve dans un point $O$ du système immobile $S$ où il y a un phare. Le phare envoie un signal chaque seconde et en effet la quantité des flashs $N$ est égale à la quantité de secondes passées en $O$. Supposons qu’un astronaute (le système en mouvement $S'$) prend le départ du point $O$. Alors, avec l’éloignement du point $O$ l’astronaute perceverra les flashs plus rarement (avec la moins fréquence), qu’avant le départ (en fait - le ralentissement du temps de phare). Cependant en approchant du phare les flashs seront plus fréquents, qu’avant le départ (maintenant - l’accélération du temps de phare). Quand $v<c$ il est évident, que l’astronaute ne peut pas dépasser ou faire le tour d’aucun flash (de sphères de la lumière). Alors indépendamment du graphique de son mouvement et de sa trajectoire, l’astronaute, ayant retourné dans le point $O$, perceverra justement $N$ quantités de flashs, c’est-à-dire tous les flashs émis par le phare. Par conséquent chaqun de ses deux observateurs confirmera que $N$ secondes passèrent sur le phare. Si l’astronaute aussi aura un phare sur sa fusée et signalera le nombre de ses secondes passées, il n’y aura pas de désaccords relativement au temps de l’astronaute. La situation est totalement symètrique (par exemple pour le paradoxe des jumeaux). En temps de la rencontre dans le même point, tous les sphères de la lumières croiseront les observateurs opposés (leur quantité ne peut pas ni augmenter, ni dimminuer). Ce nombre est $N$ - la quantité de secondes passées pour les deux observateurs.

Examinons maintenant la question d’introduction du temps uniforme absolu. (Naturellement, si on mesure le temps par le battement de son cœur, il sera subjectif et dépandera de conditions intérieurs et extérieurs). La tentative d’introduire son propre "temps électromagnétique" et l’absolutiser - c’est le retour dans le passé. Cependant, même en en ce temps là, quand malgré une vitesse misérable de la transmission de l’information (par exemple par la poste aux pigeons), les gens pouviez synchroniser le temps, parce qu’ils utiliser une source éloignée de signaux (le Soleil ou les étoiles). Imaginons une expérience suivante (Figure 1.9).

Figure 1.9: Une source infiniment éloignée pour la détermination du temps unique absolu.

Une source éloignée $S$, qui se trouve sur une perpendiculaire du milieu tracée à un segment $AB$, périodiquement envoie les signaux (avec la période $T$). En moment de l’arrivée du signal dans le point $O$ deux dispositifs enregistreurs (1 et 2) commence de se déplacer symétriquement de miroir (avec les vitesses ${\bf v}$ et ${\bf -v}$), se reflétant de $A$ et $B$ avec la période $2T$. La vitesse $v$ peut être volontaire (ça dépend du choix de la distance $AB$). Malgré ce que dans chaque moment du temps les mécanismes se déplacent l’un à l’égard de l’autre avec la vitesse $2v$ (sauf les points du reflet) les signaux seront perçus simultanément en moment du passage de point $O$ (on peut aussi y placer l’observateur 3). Le temps, ainsi déterminé sera uniforme (dans le point $O$) pour tous les trois observateurs. Avant de continuer, remarquons, que pour l’établissement des formules de la transformation de la théorie de la relativité restreinte il est suffisant d’examiner le mouvement relative le long d’une seule ligne droite (comme on examine les systèmes inertiels). Choisissant une plus grande distance $\vert SO\vert$ on peut parvenir à ce que la différence en temps entre l’arrivée du signal en point $O$ et dans les points $A$ et $B$ sera moins de n’importe quelle grandeur donnée en avant. En effet avec la précision donnée le temps sera uniforme (égal) pour tout un segment choisi $AB$ indépendement de vitesses des observateurs 1 et 2. Ainsi une source infiniment éloignée, placée perpendiculairement à la direction relative du mouvement du système peut jouer le rôle d’une horloge déterminant le temps uniforme absolu (qui est le même indépendamment du système inértiel de référence). La question du changement de la direction observée d’arrivée du signal sera exposé au dessous (pour que personne n’ait pas de tentation de tirer l’aberration, soi-disant reflétant le changement de la direction du phront de l’onde, à soi).