Le paradoxe des antipodes

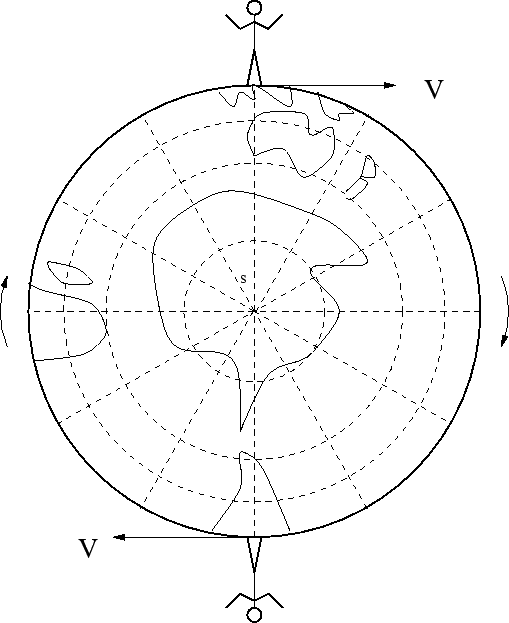
La fausseté de la théorie de la relativité restreinte se démontre facilement par la vie de l’humanité sur la Terre. Examinons la contradiction logique élémentaire de la théorie de la relativité restreinte - le paradoxe des antipodes. Deux antipodes à l’êquateur (l’un est en Brazile, l’autre est en Indonésie) se diffèrent par ce qu’à cause de la révolution de la Terre ils se dèplacent dans chaque moment du temps l’un à l’égard de l’autre avec la même vitesse modulo (Figure 1.5).

Figure 1.5: Le paradoxe des antipodes.

C’est-à-dire, malgré la symétrie évidente d’un problème chaqun d’eux doit vieillir ou rajeunir l’un relativement à l’autre. L’attraction empêche? Supposons qu’il n’y a pas d’attraction et plaçons chaqun de nos "astronauts" dans une cabine. Chaqun peut déterminer le temps sur ce "carrousel" (comme sur la Terre) dans la direction d’une étoile lointaine immobile relativement au centre de "carrousel" et par la période de sa rotation. Visiblement la marche du temps sera la même pour les deux "astronautes". On peut synchroniser le temps par la méthode spécifié (le calcul) si on connaît la période de la rotation propre du "carrousel" (toutes ses questions sont thécniques, mais pas de principes). Augmentons la vitesse linéaire $v\rightarrow c$ pour renforcer l’effet, par exemple pour que selon les formules de la théorie de la relativité reistrente la différence en marche de temps soit 100 ans en une année. La force centrifuge (l’accélération) empêche? On va agrandir le rayon de "carrousel" $R$ pour que $v^2/R\rightarrow 0$ (par exemple, même pour qu’en 100 ans l’effet intégrale de cette accélération soit moins que la précision existant de sa mesure). Alors aucune expérience ne distangera le mouvement des antipodes du mouvement rectiligne, c’est-à-dire l’absence de l’inertialité de la système ne pourra pas être découverte expérimentallement pendant tout le temps de l’expérience. Il est inutile que les relativistes luttent pour la nécessité de l’inertialité principale du système. Rappelons que même dans une telle science stricte comme la mathématique (par exemple, pour justifier la théorie des nombres réels) on utilise la notion $\varepsilon$ - le nombre infiniment petit connu d’avance. Dans notre cas pour le passage strictement mathématique le rapport de l’accélération centrifuge $v^2/R$ vers l’accélération centrifuge sur Terre $a_c$ peut être fait moins qu’une n’importe quelle grandeur infiniment petite $\varepsilon$, si on choisit un grand rayon de "carousel" (par exemple $\varepsilon\sim 10^{-10}$ ou $\varepsilon\sim 10^{-100}$, mais toutes les expériences de la théorie de la relativité restreinte sont faites sur la Terre avec $\varepsilon\sim 1$!). Ensuite si vous croyez en relativité (ou selon la théorie de la relativité restreinte, ou selon Galilée - s’est indifférent parce que nous comparons les durées), alors on peut transférer le mouvement d’un antipode parallèlement plus près de l’autre antupode et oublier du tout le modèle de carrousel. Evidemment que pour deux n’importe quels mouvements rectilignes dirigés en inverse avec les vitesses égaux par module on peut toujours faire l’opération inverse: faire un déplacement parallèle à une grande distance $R\rightarrow\infty$ d'une des trajectoires et relier le mouvement par un certain "carrousel". Ainsi qu’est ce qu’on a dans quelques années ("est-il le patient vivant")? Préférez vous plus le Brazilien ou l’Indonésien? On a la symétrie totale du problème et la chute totale de la théorie de la relativité restreinte. Il est à noter que le caractère unique du temps annule l’intransigeance de la question de son synchronisation: par exemple, on peut porter les montres avec vous. Les doutes au sujet de ce que le mouvement est "presque" inertial seront discuter au dessous, dans le Chapitre 3. Pour les relativistes qui "principalement" essayeront de fermer ces yeux et les yeux des autres à la possibilité de passage vers les plus grands $R$, on peut proposer d’inscrire dans la circonférence avec un grand $R$ un $n$-polygone régulier ($n\ge 3$; dans chaque angle il y a un obsérvateur immobile) et examiner les mouvements maintenent purement rectilignes de fusées avec des astronautes le long de côtés de ce $n$-polygone (on peut même joindre aux angles de ce $n$-polygone les lacets semblables pour l’obtention de mêmes vitesses à l’aide de mêmes accélérations "terrestres" $g$). Evidemment que pour un observateur immobile (par exempe, au centre d’une circonférence) tous ses systèmes inertiels de fusées sont tout à fait égaux et la marche du temps dans les fusée sera la même, malgré le mouvement des fusées l’une à l’égard de l’autre. Nous pouvons aussi dessiner une schéma symètrique évidente du type d’une "fleur" pour la possibilité du départ et de l’arrivée simultanés au centre de la circonférence (regardez la Figure 1.6).

Figure 1.6: Le modèle symétrique d’une fleur.

Comme nous comparons la marche du temps (mais pas le repère initial de référence du temps), on peut utiliser l’équation de la marche du temps pour n’importe quels objets en repos réciproque. Alors on peut facilement généraliser le modèle du "carrousel" pour les mouvements plats de deux objets avec de vitesses volontaires en quantité, qu’en direction. C’est un problème purement géométrique trivial (regardez la Figure 1.7).

Figure 1.7: Le modèle du carrousel pour les mouvements plats volontaires.

Par exemple nous avons deux objets, qui effectuent les mouvements linaires, représentés à la Figure 1.7 par les véctors des vitesses $\overrightarrow{AA_1}$ et $\overrightarrow{BB_1}$. Supposons que ses vitesses sont égales en module et sont proche à la vitesse de la lumière $v\rightarrow c$. Choisissons un point arbitraire $O$ dans l’espace et traçons la circonférence avec le centre dans le point $O$ de tel rayon $R$, pour que l’accélération centrifuge soit moins qu’une grandeur petite $\varepsilon_1$ (par exemple, moins qu’une exactitude existante de la mesure des accélérations): $v^2/R < \varepsilon_1$, c’est-à-dire $R > v^2/\varepsilon_1$. Traçons une droite $AA_2$ qui est perpendiculaire à $AA_1$. A travers le point $O$ traçons une droite $A_3A_4$, parallèle à la droite $AA_2$. Dans le point de d'intersection de notre circonférence et de cette ligne traçon le vécteur $\overrightarrow{A_3A_5}$, qui est égal à $\vert\overrightarrow{AA_1}\vert$ en module et parallèle à $\overrightarrow{AA_1}$. En fait nous effectuâmes tout simplement la transportation parallèlle du mouvement $\overrightarrow{AA_1}$. La procédure analogue faite avec le mouvement $\overrightarrow{BB_1}$ donne $\overrightarrow{B_3B_5}$. Maintenant les deux mouvements sont placés sur la même circonférence et ne peuvent pas étre distingueés du mouvement inertiel avec la précision existante. Par suite de la symétrie évidente du problème, il n’y aura pas du décalage horaire (temps) pour ces objets en mouvement. Par exemple, la durée du temps peut être mesurée par les flashs qui vont du centre de la circonférence $O$. Prenons maintenent le mouvement linéaire, qui se caractèrise par le vécteur de la vitesse $\overrightarrow{CC_1}$, parallèl à $\overrightarrow{AA_1}$, mais avec un autre module. Effectuons le déplacement parallèle du mouvement et recevons $\overrightarrow{C_3C_5}$ (si on prend le rayon $\vert OC_3\vert=R\vert\overrightarrow{C_3C_5}\vert/\vert\overrightarrow{A_3A_5}\vert$). Dans ce cas nous voyons, que deux objets (caractérisés par les vitesses $\overrightarrow{A_3A_5}$ et $\overrightarrow{C_3C_5}$) se déplacerons le long des arcs concentriques de circonférences $A_3a$ et $C_3d$, restant à la même distance l’un de l’autre le long des rayons de circonférences. (Sur la Figure 1.7 les arcs sont représentés comme grands seulement pour l’évidence, c’est-à-dire les mesures angulaires sont agrandises; en réalité, tous les arcs en leur mesures angulaire seront très petits et ne peuvent pas être distingués de parties droites). Il est évident que pour ses objets il n’y aura pas du décalage horaire (temps). De nouveau le temps peut être mesuré par les flashs périodiques qui vont du centre $O$ (une quantité de sphères de lumière qui passera par la circonférence $C_3d$, passera aussi par la circonférence $A_3a$ - les sphères de lumière ne "cachent, ne disparaissent, ne condensent et ne s’ajoutent" nulle part). Avec cela nous pouvons prolonger la circonférence qui passe par le point $C_3$ et tracer le vecteur $\overrightarrow{D_3D_5}$ dans n’importe quel nouvel point, tangente à la circonférence et égal en module à $\vert\overrightarrow{C_3C_5}\vert$. De nouveau les objets se déplacant avec les vitesses $\overrightarrow{D_3D_5}$ et $\overrightarrow{C_3C_5}$, se trouvent sur la même circonférence et par suite de la symétrie du problème il n’aura pas du décalage horaire (temps) pour eux. En effet s'autorisant de l'exemple du mouvement avec des vitesses $\overrightarrow{A_3A_5}$ et $\overrightarrow{D_3D_5}$ ou $\overrightarrow{B_3B_5}$ et $\overrightarrow{C_3C_5}$ on démontrea que le temps ne dépend pas ni de la grandeur, ni de la dirréction de la vitesse du mouvement plan des objets, mais s’écoule de la même manière. Le passage au mouvement tridimensionnel pour les objets s’effectue élémentairement. D’abord l’un des vecteurs de la vitesse est transporté vers le commencement du deuxième vécteur. Maintenant à travers ses deux droites d'intersection on trace un plan, dans lequel on peut faire tous les dessins décrits au-dessus. Ainsi le temps ne dépend pas du tout du mouvement réciproque des systèmes inertiels.