Certaines décisions et conséquences relativistes

Considérons le paradoxe de la transformation des forces. Supposons qu'il y a deux charges de polarité contraire stationnaires $e_1$ et $e_2$, séparées par deux surfaces planes parallèles se trouvant à la distance $L$ l’une de l’autre (Figure 4.4).

Figure 4.4: Le paradoxe de la transformation des forces.

Suite à l'attraction mutuelle des charges elles se trouvent à la distance minimale $L$ l'une de l'autre. (Elles se trouvent en équilibre indifférente par rapport aux système des surfaces planes). Mettons sur la surface au-dessus de la charge un repère où invitons des observateurs. Observons maintenant ce système des charges d'une fusée relativiste, passant avec la vitesse ${\bf v}$. Supposons que $\theta$ est un angle entre les vecteurs ${\bf v}$ et ${\bf L}$. En déterminant les forces électromagnétiques agissant entre ces charges dans le système de référence de la fusée [17], faisons attention aux composants tangentiels des forces, c'est-à-dire aux composants des forces le long des surfaces. La force

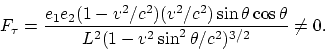$$F_{\tau} = {e_1e_2(1-v^2/c^2)(v^2/c^2)\sin\theta\cos\theta\over L^2(1-v^2\sin^2\theta/c^2)^{3/2}}\ne 0.$$ (4.1)

agit sur la charge $e_1$. En conséquence les charges se déplaceront par rapport à leur position initiale. Supposons que les bulles ont des charges énormes, $L$ est petite ($L\rightarrow 0$), et $v$ est grande ($v\rightarrow c$). Supposons que les observateurs tiennent les bulles par des fils fines. Déchireront-ils? La réponse dépend du système de référence. Qui est parmi les observateurs a raison? Donc, voilà une des contradictions de la TRR.

Considérons maintenant certains problèmes particuliers. La description du mouvement de la particule chargée $e$ au masse $m_0$ dans un champs électrique homogène constant $E_x=E$ (à voir [34]) est paradoxales du point de vue méthodique. En effet, dans la physique classique la trajectoire avec $v_y=v_0$ est une parabole

$$x = eEy^2/(2m_0v_0^2),$$

et dans la TRR elle est une caténaire

$$x = {m_0c^2\over eE}\biggl ( \cosh\biggl [ {eEy\over m_0v_0c}\biggr ] - 1\biggr ).$$

Mais avec des grand $y$ la trajectoire est proche à un exposant, c'est-à-dire elle est plus raide qu'une parabole. Et que faire avec l'idée de l'augmentation de l'inertie (de la masse) du corps avec l'augmentation de la vitesse? Même en supposant que malgré la raideur un peu plus grande, une particule passe sur la trajectoire plus lentement, quelles forces ont causé son ralentissement sur l'axe $y$? C'est que la force $F_y=0$ et dans la TRR elle n'existe non plus: $F'_y=0$. Et la valeur de la vitesse initiale $v_y=v_0$ peut être non-relativiste (et restera pareille).

La balance de l'énergie de la fusée relativiste est étrange [33]:

$$m\cosh\theta + M_2\cosh(d\theta) = M_1.$$

Avec une grande vitesse de la projection ($\theta=\tanh(v/c)$) pour la valeur limité des masses $M_1$ initiale et $M_2$ finale la condition suivante doit être réalisée: la masse de la projection isolée $m\rightarrow 0$ (pour la non-contradiction de la TRR). Pourtant cette grandeur ne se définit que par l'équipement technique de la fusée: il n’y a pas de limites de principes.

Une des déductions d'Einstein de la formule $E=mc^2$ n’est pas assez argumentée. Dans cette déduction le processus de l'absorption du corps des deux impulsions symétriques de la lumière est considéré du point de vue des deux observateurs, qui sont en mouvement l'un par rapport à l'autre. Le premier ne bouge pas par rapport au corps et le deuxième est en mouvement perpendiculaire à la lumière (Figure 4.5).

Figure 4.5: A la déduction de la formule $E=mc^2$.

Selon la TRR la lumière doit être d'avance au courant du mouvement de l'observateur avec la vitesse $v$ et recevoir une impulsion pour que dans ce deuxième système la vitesse du corps ne change pas, tandis que la masse doit changer. Et que faire avec les expériences de Lebedev (et avec les idées contemporaines généralement admises) sur la pression de la lumière lors desquelles pendant le transfert de la lumière de l'impulsion la vitesse du corps observé changeait? Et quels changements l’impulsion subira si on a des surfaces absolument absorbantes et inégales (biseautés)? Il n’est pas claire non plus sur les dessins annexés s'il s'agit de la lumière réelle transversale (le modèle admis pour aujourd’hui dans la TRR aussi) ou de la lumière transversale-longitudinal mystique (pour le sauvetage de la TRR).

La différence de la masse de l'émission commune d'après l'impulsion du système est aussi un peu étrange dans la TRR contemporaine:

$$m = \sqrt{{(E_1+E_2)^2\over c^4} -{({\bf P}_1+{\bf P}_2)^2\over c^2}}.$$ (4.2)

Et si nous changeons l'impulsion (la direction) des quanta de lumière isolés pas des miroirs? Et mettons à part le centre de gravité du système? Où sera-t-elle localisée et quelle sera la structure du champ de près? Est-il possible que ce centre sautera, disparaîtra et apparaîtra de nouveau? A l'aide de la formule citée de la TRR (4.2) pour la définition de la masse de l'émission commune des deux quanta de lumière sous un angle volontaire, considérons l'émission provenant d’un centre (Figure 4.6).

Figure 4.6: La masse de la combinaison des photons.

Alors on peut recevoir la masse commune différent de tout le système (ne faudra-t-il pas introduire d'une manière artificielle des masses négatives pour "l'explication" de toutes les variations possibles de la masse?) en dépendance du groupement par deux des quanta. Et dans la TRG il faut faire attention à la préhistoire de la naissance de l'émission pour la définition de la position de son centre de gravité et la structure espace-temps inconnue du champ électromagnétique pour la vraie description de l'autre phénomène: la gravité? Cela est extrêmement difficile!