Les équations de Maxwell

Une petite remarque suivante concerne des équations de Maxwell (leurs formes contemporaines et généralement admises). Rappelons-nous qu'elles ont été reçues par moyen de la généralisation phénoménologique des faits expérimentaux aux vitesses minimes (par analogie avec l'hydrodynamique). En conséquence il ne faut pas estimer qu'elles sont en forme finale. Les équations de Maxwell (où les équations d'ondes) définissent la vitesse de phase, tandis que la théorie de la relativité prétend l'existence de la vitesse maximale des signaux (la vitesse collective). En effet, nous toujours travaillons avec la lumière concrète, c'est pourquoi ce fait doit être marqué par un certain index: au lieu de $c$ il faut écrire la dépendance paramétrique $c(\omega)$ et l'équation d'ondes sera équation pour une Fourier-harmonique. Vu que les adeptes contemporains du relativisme renoncent à l'évidence et à la nécessité des modèles du milieu de la diffusion de la lumière, la voie de la généralisation des équations de Maxwell pour "la vacuité absolue" dans le cas de la lumière polycinétique, devient multiforme. Sans parler du passage aux milieux non-linnéaires réels (avec des particularités de la "vacuité intermoléculaire", les mécanismes de l'absorption et de la rémission de la lumière par les molécules etc.): sans principes physiques et ne tenant compte que des raisons mathématique, on peut pas faire beaucoup de généralisations pareilles et elles toutes serons égales. L'exigence de l'invariance des équations de Maxwell relativement aux transformations des coordonnées et du temps et assez vacillante, parce qu'on peut introduire des champs et les équations pour eux par beaucoup de moyens à seule condition de la correspondance des influences mesurées des ces champs aux grandeurs observées dans les expériences. Par exemple, dans [81] est montré l'existence des transformations non-locales des champs, qui conservent les équations de Maxwell avec le temps constant. Dans [14] on montre qu'on peut introduire des transformations non-linnéaires et non-locales pour que les équations du champs soient invariantes relativement aux transformations de Galilée lors des transformations déterminées.

Montrons une contradiction méthodique des transformations généralement admises des champs. Supposons, qu'il y a deux fils neutres infinis et parallèles. Et dans tous les deux fils des électrons se meuvent dans la même direction avec une vitesse constante relativement à une charpente positivement chargée, c'est-à-dire, il s'agit de la même densité des courants ${\bf j}$. Alors pour le cas classique dans la formule du champ la grandeur

$$jdV = en(v_{+} - v_{-})dV$$

est invariante, c'est-à-dire le champ ${\bf H}_{\perp}$ et l'influence de ce champ ne dépendent pas du mouvement du système. Du point de vue relativiste (étant donné que ${\bf E}=0$), nous avons

$$H_{\perp} = {H_{\perp}^0\over \sqrt{1-v^2/c^2}},$$

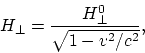
c'est-à-dire le champ dépend de la vitesse du mouvement de l'observateur. Pourtant deux cas suivants sont évidemment égaux:
(1) le système avec la vitesse ${\bf v}_{obs} = 0$, c'est -à-dire, l'observateur repose relativement à la charpente et les électrons se meuvent avec la vitesse ${\bf v}$, et
(2) le système se déplace avec la vitesse ${\bf v}_{obs} = {\bf v}$, c'est-à-dire l'observateur repose relativement aux électrons et la charpente (les ions positivement chargés) se déplace dans la direction contraire avec la vitesse $-{\bf v}$ (le même courant). Une formule relativiste donne à ces deux cas les valeurs différentes de ${\bf H}_{\perp}$ (et des influences des champs), ce qui est absurde. De plus la description dans la TRR des passages d'un système inertiel à un autre pour la situation tridimensionnelle avec des courants non-neutres (avec des faisceaux des particules chargées).

Passons maintenant à la question "principale" de l'invariance des équations de Maxwell, bien publicitaire dans la TRR. L'invariance des équations de Maxwell par rapport aux transformations de Lorentz ne signifie rien pour les autres phénomènes. Premièrement, les équations de Maxwell sont des équations pour les champs en espace vide. Dans l'espace pareil nous pouvons couper la moitié du morceau et après l'avoir multiplié par 2 nous recevront le même morceau. Voilà pourquoi dans l'espace mathématique vide on peut utiliser n'importe quel système de référence, des géométriques cohérentes et des coefficients de passage (transfert). Cela ne se définit que par les commodités de la description mathématique. Pourtant nous ne pouvons pas couper un organisme vivant et l'augmenter en 2 fois sous un microscope, l'organisme moura. La présence dans l'espace des corps et des champs physiques réels crée des points de repère naturels, des proportions caractéristiques et des corrélations des objets. Tout cela définit la différence de l'espace physique réel et l'espace mathématique vide. Deuxièmement, la particularité des certaines interactions de se propager dans le vide avec la vitesse de lumière ne détermine pas la vitesse de la propagation des interactions dans le milieu. Malgré un grand rôle des interactions électromagnétiques, la perturbation dans les milieux se répand avec la vitesse du son. Il est impossible de déterminer par une seule constante $c$ se rapportant au vide (pour notre monde "électromagnétique") la vitesse du son et de la lumière dans le gaz, le liquide et le corps solide. Il n'est pas claire comment l'anisotropie des corps solides réels a pu apparaître dans l'espace isotrope. Toutes ces particularités et beaucoup d'autres sortent des bornes de l'application des équations de Maxwell dans le vide (tandis que la TRR propose le "clonage" des particularités du vide aux toutes les particularités des milieux et des corps matériaux). Par conséquent, rapprocher les particularités du monde à l'invariance des équations de Maxwell dans le vide est une prétention exagérée de la TRR. Troisièmement, la division du champ unique (intact) par son influence en parties électrique et magnétique est éventuelle et (suffisamment) volontaire. Voilà pourquoi l'invariance de ces parties, mises à part artificiellement, ne peut pas avoir une importance décisive. La présence des coefficients $\rho,\varepsilon,\mu$ (dépendant des coordonnées, du temps, des particularités de la lumière etc.) pour les équations de Maxwell dans le milieu fait ces équations non-invariantes par rapport aux transformations de Lorentz (où il faut abolir l'objectivité des caractéristiques du milieu).