L'énergie et l'impulsion dans la TRR

Commençons par la remarque sur l'unité de mesure. L'expression de l’impulsion et de l'énergie dans des unités de mesure de la masse n'est pas utile, car ces grandeurs ne sont pas interchangeables, et malgré ce que le nombre d’opérations (et de combinaisons) collectifs avec eux est limité, on est oblige de les considérer comme des grandeurs physiques différentes. Faut-il confondre le système des unités de mesure bien structuré?

L'approche de la TRR à la dynamique relativiste, est-elle unique? Bien sur que non! Dans la physique classique la division de l'énergie en énergie cinétique et potentielle est un peu conventionnelle. Par exemple, dans la physique classique lors de la description du mouvement dans des systèmes tournants non inertiels on prend pour l'énergie potentielle l'énergie cinétique (!) moyenne du mouvement du système: de $v_{\varphi}=\Omega\rho$ est fait $E_{pot}=m\Omega^2\rho^2/2$. Il existe un autre exemple spectaculaire de l'hydrodynamique, quand on introduit la notion de la masse attaché - "effective") pour la description du mouvement du corps à travers le milieu. Il est claire que la vrai masse n'a pas changé dans ce cas. Dans la mécanique relativiste le complément "rapide" à l’accélération peut être lié à l'énergie potentielle du corps et l'énergie cinétique du corps peut rester sans changements et on peut considérer les équations classiques de Newton, mais avec une autre force "effective" et la masse constante $m_0$.

Malgré les affirmations de la TRR de l'importance de l'introduction des 4-vecteurs, même pour les trois particules en interaction, la formule

$$E = \sum_i m^{(i)}c^2\gamma^{(i)}, ~ ~ ~ ~ {\bf P} = \sum_i m^{(i)}{\bf v}^{(i)}\gamma^{(i)},$$

où

$$\gamma^{(i)} = {1\over \sqrt{1-v_i^2/c^2}}$$

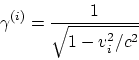
ne composent pas le 4-vecteur et ne se conservent pas. L'introduction de l'énergie potentielle de l'interaction des particules provoque aussi des difficultés. La TRR, serait-elle une théorie des deux corps? Où est alors son caractère général (universel) déclaré? De pareilles difficultés surgissent lors de la construction des fonctions de Lagrange et de Gamilton pour les systèmes des particules en interaction.

Le passage limite à l'énergie classique est aussi contradictoire. Les conditions de ce passage ont été déjà citées $c\rightarrow\infty$. Mais dans ce cas non seulement l'énergie de repos, mais n'importe quelle énergie sera $E=\infty$ dans la TRR. L'inscription de l'impulsion relativiste [26] comme ${\bf P}=m(d{\bf r}/d\tau)$ n 'est pas valable non plus, car $d{\bf r}$ se rapporte au système de référence immobile, tandis que $d\tau$ (le temps lui-même) se rapporte au système en mouvement (corps).

Le passage limite aux vitesses minimes pour un grand nombre de grandeurs pose beaucoup de questions. Toutes les formules doivent passer à la forme de Newton, quand la vitesse de la transmission des interaction est supposée comme infinie (la fonction de Lagrange, l'action, l'énergie, la fonction de Gamilton etc.). Pourtant, nous voyons [17], que ce n'est pas vrai: la 4-vitesse passe dans l'ensemble de chiffres (1,0,0,0) et ne signifie rien, la 4-accélération non plus; l'intervalle $S\rightarrow\infty$ et la grandeur ds dépendent de l'ordre du passage limite; des components de la 4-force tendent à la composition (ensemble) zéro etc. Cela bien montre que toutes les grandeurs et les formules relativistes citées ne peuvent par avoir leurs sens physique indépendant.