Energie und Impuls in der SRT

Beginnen wir mit der Bemerkung betreffs der Maßeinheiten. Der Ausdruck von Impuls und Energie in Einheiten von Masse kann nichts Nützliches geben, weil diese Größen gegenseitig nicht austauschbar sind, die Zahl der gemeinsamen Operationen mit ihnen (und Kombinationen) begrenzt ist, einerlei soll man ihnen als verschiedenen physischen Größen achtgeben. Ob es sich lohnt, Verwirrung in die ziemlich gut angepassten Einheiten von Dimensionen anzustiften?

Ist das SRT-Herangehen an die relativistische Dynamik das einzige? Ganz und gar nicht! In der klassischen Physik kann die Teilung von Energie in kinetische und potentielle ziemlich bedingt sein. In der statistischen Physik, z.B., rechnet man bei der Beschreibung der Bewegung in nichtinertialen rotierenden Systemen der potentiellen Energie die durchschnittliche kinetische (!) Bewegungsenergie des Systems zu: aus $v_{\varphi}=\Omega\rho$ ist $E_{pot}=m\Omega^2\rho^2/2$ gebildet. Es gibt ein anderes lehrreiches Beispiel von Hydrodynamik, wenn der Begriff von eingeschlossener („effektiver“) Masse für die Beschreibung der Bewegung des Körpers durch das Medium eingeführt wird. Klar, dass sich die wirkliche Masse in diesem Fall nicht ändert. Genauso kann der neue „Schnell“zusatz zur Beschleunigung in der relativistischen Mechanik mit der potentiellen Energie des Körpers verbunden sein, die kinetische Energie des Körpers kann man unverändert lassen und die klassischen Gleichungen von Newton, aber mit einer anderen „effektiven“ Kraft und der konstanten Masse betrachten.

Trotz den SRT-Behauptungen von Wichtigkeit und Notwendigkeit der Einführung von 4-Vektoren bilden die Ausdrücke

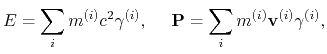
$\displaystyle E = \sum_i m^{(i)}c^2\gamma^{(i)}, ~ ~ ~ ~ {\bf P} = \sum_i m^{(i)}{\bf v}^{(i)}\gamma^{(i)},$

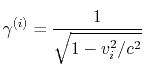
$\displaystyle \gamma^{(i)} = {1\over \sqrt{1-v_i^2/c^2}}$

sogar für drei wechselwirkende Teilchen keine 4-Vektoren und werden nicht erhalten. Kompliziertheiten ruft auch die Einführung der Potentialenergie der Wechselwirkung von Teilchen hervor. Kann das denn stimmen, dass die SRT die Theorie von zwei Körpern ist? Wo ist denn die deklarierende Gesamtheit (Universalität)? Gleichartige Kompliziertheiten entstehen beim Aufbau der Funktionen von Lagrange und Hamilton für Systeme der wechselwirkenden Teilchen.

Der Grenzübergang zur klassischen Energie ist auch widerspruchsvoll. Es wurde oben von der Bedingung eines solchen Übergangs $c\rightarrow\infty$ gesagt. Aber dann nicht nur die Ruhenergie, sondern jede Energie wird in der SRT $E=\infty$ sein. Nicht konsequent ist auch die Aufzeichnung des relativistischen Impulses in der Form [26] ${\bf P}=m(d{\bf r}/d\tau)$ , weil $d{\bf r}$ zum ortsfesten Bezugssystem und $d\tau$ (Eigenzeit) zum bewegten System (Körper) gehört.

Der Grenzübergang zu kleinen Geschwindigkeiten ruft eine Reihe von Fragen für viele Größen hervor. Alle Formeln sollen zur Newtonschen Form überwechseln, wenn die Übertragungsgeschwindigkeit von Wechselwirkungen endlos vorausgesetzt wird (z.B., die Lagrange-Funktion, Wirkung, Energie, Hamilton-Funktion u.a.). Wir sehen aber [17], dass es nicht so ist: die 4-Geschwindigkeit geht in den Satz von vier Zahlen (1,0,0,0) über und bedeutet nichts, die 4-Beschleunigung auch; das Intervall $S\rightarrow\infty$ und die Größe hängen von der Ordnung des Grenzübergangs ab; sie streben nach dem Nullsatz der Komponente 4-Kräfte usw. Das zeigt anschaulich, dass alle erwähnten relativistischen Größen und Ausdrücke den selbständigen physischen Sinn nicht haben können.

Artecha S.N.