Maxwell-Gleichungen

Folgende kurze Bemerkung betrifft die Maxwell-Gleichungen (ihre gegenwärtige allgemeingültige Form). Wir erinnern Sie daran, dass die durch phänomenologische Verallgemeinerungen der experimentellen Fakten bei kleinen Geschwindigkeiten erhalten wurden (es wurde die Analogie mit Hydrodynamik genommen). Folglich lohnt es sich nicht zu warten, dass sie in endgültiger Form erraten wurden. Die Maxwell-Gleichungen (oder Wellengleichung) bestimmen die Phasengeschwindigkeit, während die Relativitätstheorie „Ansprüche“ auf die maximale Geschwindigkeit von Signalen (Gruppengeschwindigkeit) erhebt. In der Tat haben wir immer mit dem konkreten Licht zu tun, deswegen soll diese Tatsache durch einen Index gezeichnet werden: statt $c$ soll man Parameterabhängigkeit $c(\omega)$ schreiben, und die Wellengleichung wird zur Gleichung des harmonischen Obertons von Fourier. Da die heutigen Apologeten des Relativismus auf Anschaulichkeit und prinzipielle Notwendigkeit von Modellen der Lichtfortpflanzungsmedien verzichten, wird der Weg von Verallgemeinerung der Maxwell-Gleichungen sogar für die „absolute Leere“ im Falle des nicht monochromatischen Lichtes, geschweige denn den Übergang zu realen nicht linearen Medien (die die Eigenschaften der „zwischenmolekularen Leere“, Mechanismen von Absorption und Widerausstrahlung usw. in sich einschließen )nicht eindeutig: ohne physische Prinzipien, aus rein mathematischen Überlegungen kann man soviel man will solcher Verallgemeinerungen einführen, und sie werden alle gleichberechtigt. Die Forderung der Invarianz der Maxwell-Gleichungen bezüglich der Transformationen von Koordinaten und Zeit ziemlich schwankend ist, weil Felder und Gleichungen für sie durch eine Menge von Vorgehen einführen kann, wenn nur die gemessenen Einwirkungen dieser Felder den real in Experimenten beobachtenden Größen entsprechen würden. So, z.B., in [81]ist gezeigt, dass nicht lokale Transformationen von Feldern existieren, die die Maxwell-Gleichungen mit unveränderter Zeit erhalten. In [14] ist gezeigt, dass man nicht lineare und nicht lokale Transformationen einführen kann, damit die Feldgleichungen bei bestimmten Transformationen von Feldern invariant bezüglich der Galilei-Transformationen waren.

Wollen wir den methodischen Widerspruch von allgemeingültigen Transformationen für Felder demonstrieren. Mögen zwei endlose nicht geladene parallele Leiter. Es sollen sich Elektronen in beiden Leitern in einer Richtung mit konstanter Geschwindigkeit bezüglich des positiv geladenen Rumpfes bewegen, d.h., wir haben gleiche Dichten von Strömen j. Im Ausdruck für Feld im klassischen Fall ist dann die Größe

$$jdV = en(v_{+} - v_{-})dV$$

eine Invariante, d.h., das Feld $H_{\perp}$ und die Einwirkung dieses Feldes hängen von der Geschwindigkeit der Bewegung des Systems nicht ab. Für die relativistische Betrachtung (da ${\bf E}=0$) haben wir

$$H_{\perp} = {H_{\perp}^0\over \sqrt{1-v^2/c^2}},$$

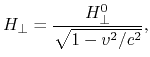
d.h., das Feld hängt von der Bewegungsgeschwindigkeit des Beobachters ab. Doch sind zwei folgende Fälle offensichtlich gleichberechtigt:
(1) das System mit der Geschwindigkeit ${\bf v}_{beo}=0$, d.h., der Beobachter ruht bezüglich des Rumpfes, und die Elektronen bewegen sich mit der Geschwindigkeit ${\bf v}$, und
(2) das System bewegt sich mit der Geschwindigkeit ${\bf v}_{beo}={\bf v}$, d.h., der Beobachter ruht bezüglich der Elektronen, und der Rumpf (positive Ionen) bewegt sich in entgegengesetzter Richtung mit der Geschwindigkeit $-{\bf v}$ (derselbe Strom). Die relativistische Formel gibt für diese Fälle verschiedene Größen $H_{\perp}$ (und Feldeinwirkungen), was absurd ist. Außerdem erweist sich die SRT-Beschreibung der Übergänge von einem Inertialsystem zum anderen für dreidimensionale Situationen mit nicht neutralen Strömen (z.B., mit Bündeln von geladenen Teilchen) ganz widerspruchsvoll.

Klären wir jetzt die „grundsätzliche“ Frage von der Invarianz der Maxwell-Gleichungen, die in der SRT großgeschrieben wurde. Die Invarianz der Maxwell-Gleichungen bezüglich der Lorentz- Transformationen bedeutet ganz und gar nichts für andere Erscheinungen. Erstens sind die Maxwell-Gleichungen Gleichungen für Felder im leeren Raum. Im solchen Raum können wir eine Hälfte der Strecke abschneiden und verdoppeln, wir bekommen dieselbe Strecke. Deshalb kann man im leeren mathematischen Raum beliebige Bezugssysteme, nicht widersprechende Geometrien und Umrechnungsfaktoren anwenden. Das kann nur durch Bequemlichkeit der mathematischen Beschreibung bestimmt werden. Wir können doch den lebendigen Organismus einfach nicht aufschneiden und unter dem Mikroskop doppelt vergrößern – der Organismus wird sterben. Das Vorhandensein realer physischer Körper und Felder im Raum gibt natürliche Festpunkte, kennzeichnende Maßstäbe und Wechselwirkungen zwischen Objekten vor. Dies alles legt den Unterschied des realen physischen Raums vom leeren mathematischen Raum fest. Zweitens determiniert die Eigenschaft mancher Wechselwirkungen, sich im Vakuum mit der Lichtgeschwindigkeit zu verbreiten, die Geschwindigkeit der Verbreitung von Wechselwirkungen im Medium nicht. Trotz der großen Rolle der elektromagnetischen Wechselwirkungen verbreiten sich Störungen in Medien mit der Schallgeschwindigkeit. Nach einer Konstanten $c$, die zum Vakuum gehört, ist es unmöglich (für unsere „elektromagnetische“ Welt), Geschwindigkeiten von Schall und Licht in Gasen, Flüssigkeiten und Festkörpern zu bestimmen. Es ist nicht klar, wie die Anisotropie der realen Festkörper im isotropen Raum entstehen könnte. All die und viele andere Eigenschaften überschreiten die Grenzen der Anwendbarkeit der Maxwell-Gleichungen in der Leere (die SRT schlägt doch das Klonen der Eigenschaften der Leere auf alle Eigenschaften von materiellen Körpern und Medien vor). Die Anpassung der Eigenschaften der ganzen Welt an die Invarianz der Maxwell-Gleichungen in der Leere ist folglich zu überhöhter Anspruch der SRT. Drittens ist die Teilung des seiner Wirkung nach einheitlichen Feldes in den elektrischen und den magnetischen Teil ziemlich bedingt und in bedeutendem Maße willkürlich. Deswegen kann die Invarianz dieser künstlich gewählten Teile keine entscheidende Bedeutung haben. Das Vorhandensein von Faktoren $\rho, \epsilon, \mu$ (die von Koordinaten, Zeit, Lichteigenschaften u.a. abhängen) für die Maxwell-Gleichungen im Medium macht diese Gleichungen bezüglich der Lorentz- Transformationen nicht invariant (oder man soll wieder die Objektivität der Charakteristiken vom Medium abschaffen).