La paradoja de los antípodas

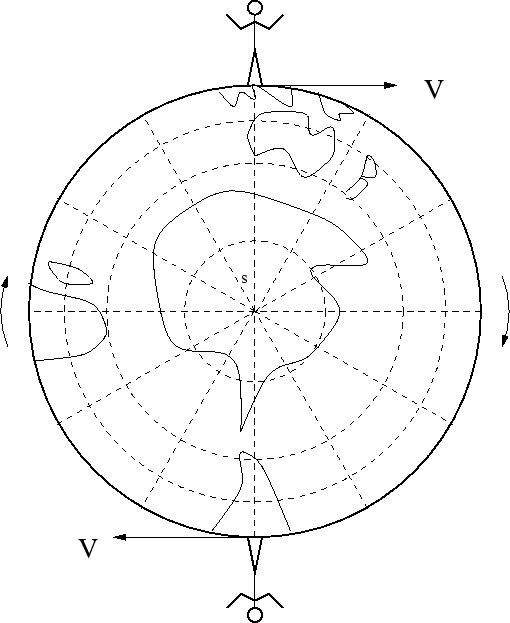
La falsedad de la TER se demuestra de forma simple con ayuda del tiempo de la vida completa de la hunmanidad sobre el planeta Tierra. Analicemos la contradicción lógica elemental de la TER: la paradoja de los antípodas. Dos antípodas en el ecuador (uno en Brasil, por ejemplo, y el otro en Indonesia) se distinguén porque, a consecuencia de la rotación de la Tierra, se mueven uno respecto al otro en cada momento de tiempo a una velocidad constante en su módulo (Fig. 1.5).

Figura 1.5: La paradoja de los antípodas.

Luego, a pesar de la evidente simetría del problema, cada uno de los dos debe envejecer o rejuvenecer con respecto al otro. ¿Interfiere la fuerza de gravedad? Quitémosla y coloquemos a cada uno de nuestros " astronautas" en una cabina. El tiempo en tal "carrusel" puede ser establecido por cada uno de ellos (como sobre la Tierra) tomando en cuenta la direción hacia una estrella lejana inmóbil, con respecto al centro del carrusel, y mediante el período de rotación propia del carrusel. Obviamente, el transcurso del tiempo será igual para ambos "cosmonautas". El tiempo se puede sincronizar con ayuda de un método de cómputo, conociendo el período de rotación (estas no son cuestiones fundamentales, sino simplemente técnicas). Aumentemos la velocidad lineal $v\rightarrow c$ para amplificar el efecto, por ejemplo, para que mediante las fórmulas de la TER la diferencia en el transcurso del tiempo consista en 100 años por cada año. ¿Estorba la fuerza (aceleración) centrífuga? Aumentemos el radio del carrusel $R$ de modo que $v^2/R\rightarrow 0$ (para que, por ejemplo, incluso en 100 años el efecto integral de tal aceleración sea en muchos órdenes menor que la exáctitud existente de su medición). Entonces ningún experimento podrá diferenciar el movimiento de los antípodas del movimiento rectilineo, es decir, el caracter no inercial del sistema no puede ser observado experimentalmente en todo el tiempo en que se realiza la prueba. No vale la pena luchar contra los relativistas por la necesidad de una inercialidad categórica del sistema. Recordemos que incluso en una ciencia tan estricta como las matemáticas (por ejemplo, al fundamentar la teoría de los números reales) se utiliza el concepto de $\varepsilon$: un número dado con antelación tan pequeño como sea posible. En nuestro caso, para el paso estrictamente matemático, la relación de la aceleración centrífuga $v^2/R$ con respecto a la aceleración centrífuga sobre la Tierra $a_{c}$ puede hacerce menor que cualquier valor $\varepsilon$ tan peuqeño como se quiera a cuenta de la elección del radio mayor del "carrusel" $R$ (por ejemplo, se puede tomar $\varepsilon\sim 10^{-10}$ o $\varepsilon\sim 10^{-100}$, ¡pues todos los experimentos de la TER se ha realizado cobre la Tierra con $\varepsilon\sim 1$!). Prosiguiendo, si usted cree en la relatividad (ya según la TER ya según Galileo, es indistinto, puesto que estamos comparando duraciones), entonces el movimiento de uno de los antípodas se puede trasladar paralelamente más cerca del otro antípoda y olvidarnos completamente del modelo del carrusel. Evidentemente, para cualesquiera dos direcciones diametralmente opuestas y de igual módulo de velocidad siempre se puede realizar mentalmente la operación contraria: llevar a cabo el traslado paralelo de una de las trayectorias hasta una gran distancia $R\rightarrow\infty$ y atar los movimientos a un cierto "carrusel". Asi pues, dentro de algunos años "¿vive aún el paciente o está muerto?" ¿Y quién les gusta más, el brasileño o el indonés? Para una completa simetría del problema, un completo derrumbe de la TER. Destaquemos que, hablando en general, el carácter único del tiempo anula el carácter fundamental de la pregunta acerca de su sincronización: el reloje, por ejemplo, se puede llevar consigo. Las dudas respecto a la "casi" inercialidad del movimiento serán discutidas más adelante, en el Capítulo 3. Y para aquellos relativistas que cerrarán categóricamente los ojos a sí mismos y a otros ante la posibilidad de pasar a los grandes R se les puede sugerir que dentro de una circinferencia de radio grande inscriban un n-ágono (n>3; en cada ángulo se encuentra un observador inmóvil) y que consideren ahora los movimientos ya puramente rectilíneos de las naves con los astronautas a lo largo de los lados de este n-ágono (incluso lazos iguales para un conjunto de velocidades iguales con ayuda de iguales aceleraciones terrestres g pueden ser sujetados a los ángulos de este n-ágono). Evidentemente, para el observador inmóvil (por ejemplo, en el centro de la circunferencia) todos estos sistemas inerciales de cohetes son completamente equitativos y el transcurso del tiempo en las naves será igual, a pesar del movimiento de las naves unas respecto a otras. También podermos dibujar el evidente esquema simétrico del tipo "flor" para la posibilidad de un arranque y arribo simultáneos de los astronautas desde el centro de la circunferencia (ver la Fig. 1.6).

Figura 1.6: El modelo simétrico de la "flor".

Puesto que estamos comparando el transcurso del tiempo (y no su orígen de coordenadas), se puede utilizar la igualdad del trancurso del tiempo para cualesquiera objetos en reposo mutuo. Entonces el modelo del carrusel puede ser fácilmente generalizado para el caso de los movimientos planos de dos objetos con velocidades arbitrarias en módulo y en dirección. Esta es una taréa trivial puramente geométrica (Fig. 1.7).

Figura 1.7: El modelo del carrusel para movimientos planos arbitrarios.

Por ejemplo, sea que tenemos dos objetos que realizan movimientos rectilíneos, representados en la Fig. 1.7 mediante los vectores de velocidad $\overrightarrow{AA_1}$ y $\overrightarrow{BB_1}$. Supongamos que estas velocidades son iguales en módulo y que su magnitud es cercana a la de la luz $v\rightarrow c$. Elijamos en el espacio un punto arbitrario $O$ y tracemos una circunferencia con centro en $O$ y de radio $R$ tal que la fuerza centrífuga sea menor que un cierto valor pequeño $\varepsilon_1$ dado de antemano (por ejemplo, la exactitud existente para la medición de la aceleración): $v^2/R<\varepsilon_1$, es decir $R>v^2/\varepsilon_1$. Tracemos la recta $AA_2$ perpendicular a la recta $AA_1$. Pasando por el punto $O$, tracemos la recta $A_3A_4$ paralela a la recta $AA_2$. En el punto de intersección entre nuestra circunferencia y dicha recta tracemos el vector $\overrightarrow{A_3A_5}$, igual en módulo a $\vert\overrightarrow{AA_1}\vert$ y paralelo a $\overrightarrow{AA_1}$. Prácticamente sólo trasladamos paralelamente el movimiento $\overrightarrow{AA_1}$. Realizando un procedimiento análogo con el movimiento $\overrightarrow{BB_1}$ obtenemos $\overrightarrow{B_3B_5}$. Ahora ambos movimientos se encuentran sobre una misma circunferencia y con la exactitud experimental existente no pueden ser distinguidos del movimiento inercial. A consecuencia de la evidente simetría del problema, el tiempo para tales objetos en movimiento transcurrirá de igual manera. La duración del tiempo puede medirse, por ejemplo, mediante resplandores periódicos que provengan del centro $O$ de la circunferencia. Tomemos ahora el movimiento rectilíneo caracterizado por el vector $\overrightarrow{CC_1}$, paralelo a $\overrightarrow{AA_1}$ pero con diferente módulo. Realicemos el traslado paralelo y obtengamos $\overrightarrow{C_3C_5}$ (tomando el radio $OC_3\vert=R\vert\overrightarrow{C_3C_5}\vert/\vert\overrightarrow{A_3A_5}\vert$). En este caso veremos que dos objetos (caracterizados por las velocidades $\overrightarrow{A_3A_5}$ y $\overrightarrow{C_3C_5}$) se moverán a lo largo de los arcos concéntricos $A_3a$ y $C_3d$, rezagándose uno respecto al otro una misma distancia a lo largo de los radios de las circunferencias. (En la Fig. 1.7 se han representado arcos grandes sólo con fines aclarativos, es decir, se han aumentado sus dimensiones angulares; en realidad, todos los arcos tendrán dimensiones angulares muy pequeñas e indistinguibles de los segmentos rectilíneos). Obviamente, el tiempo para tales objetos también transcurrirá igual. Nuevamente, el tiempo puede "medirse" con ayuda de destellos períodicos del centro O (cuantas esferas de luz pasen por la circunferencia $C_3d$, tantas otras pasarán también por la circunferencia $A_3a$. Las esferas de luz no se ocultan en ningún lado, "no desaparecen ni se condensan ni se agregan"). Aquí nosotros podemos continuar la circunferencia que pasa por el punto $C_3$ y en cualquier nuevo punto trazar el vector $\overrightarrow{D_3D_5}$, tangencial a la circunferencia e igual en módulo a $\vert\overrightarrow{C_3C_5}\vert$. Nuevamente, los objetos que se mueven con velocidades $\overrightarrow{D_3D_5}$ y $\overrightarrow{C_3C_5}$ se ubican en una misma circunferencia y, a consecuencia de la simetría del problema, el tiempo transcurrirá de igual manera para ambos. En suma, con ayuda del ejemplo de los movimientos cuyas velocidades son $\overrightarrow{A_3A_5}$ y $\overrightarrow{D_3D_5}$ o $\overrightarrow{B_3B_5}$ y $\overrightarrow{C_3C_5}$, hemos demostrado que el tiempo no depende en absoluto ni de la magnitud ni de la dirección del movimiento plano de los objetos, sino que transcurre de igual manera. El paso al movimiento tridimencional para objetos puntuales se lleva a cabo de la misma forma elemental. Inicialmente uno de los vectores de la velocidad se traslada al orígen del segundo vector. Después, a través de estas réctas que se intersectan se traza un plano, en el cual se pueden realizar todas las construcciones descritas anteriormente. De esta manera, el tiempo no depende en absoluto del movimiento mutuo de los sistemas inerciales.