En los apéndices se analizarán algunas hipótesis particulares. Ellas prácticamente no están relacionadas con la crítica a la teoría de la relatividad, expuesta en la parte principal de este libro, acaso demuestran que el de la TER no es el único planteamiento y que es posible la parametrización por frecuencias de los cálculos. En el presente libro los Apéndices sólo prentenden esto, ya que utilizan los métodos incorrectos de la TER (su falsedad se demostró en los capítulos principales de este libro). Con las ideas expuestas en los primeros dos apéndices ( y con parte del análisis del experimento de Michelson del Capítulo 3), el autor intentó acceder a varias revistas ampliamente conocidas desde el año 1993 hasta el año 1999. Y ya sea que el trabajo diplomáticamente no era revisado enseguida, ya llegaba aproximadamente tal respuesta: "Nadie ha observado nada semejante en la teoría de la relatividad ni en la electrodinámica cuántica, y la exactitud de las predicciones de estas teorías es enorme". ¿Cómo puede en general un físico teórico observar algo nuevo (y no explicarlo "con posterioridad")? El debe presuponer cierto hecho y comprobar las consecuencias de su suposición. Pero nadie ha siquiera intentado suponer la posibilidad de la dependencia de la velocidad de la luz con respecto a la frecuencia. Además, se mencionaba a una exáctitud que fuese en uno o dos órdenes mayor que la exactitud de los experimentos actuales. Tal exactitud puede ser alcanzada en un corto tiempo pues en la física se discuten seriamente los experimentos que exigen una exactitud de unas cuantas decenas de órdenes mayor que la actual. Finalmente, el autor se cansó de perder el tiempo y decidió comprobar qué exactitud tan grande es esa de la teoría de la relatividad (de paso se recuerda la insatisfacción estudialtil propia con esta teoría). Como resultado apareció el primero de los artículos críticos propios y ahora este libro. Así que, todo tiene su parte positiva y su parte negativa.
Pasemos ahora a la discusión de la posible dependencia de la velocidad de la
luz respecto a la frecuencia. Se sabe que al colocar una partícula en el vacío
en éste ocurren diferentes procesos tales como la aparición de pares virtuales
(partícula-antipartícula); muchos procesos de interacción pueden ser descritos
con el uso de tales pares virtuales. Durante su proceso de difusión, la luz
también influye en las propiedades del vacío (en particular, deberá tener lugar
la polarización del vacío). Luego, según el principio de correspondencia deberá
haber una acción retroactiva del vacío polarizado sobre el proceso de difusión
de la luz. Como resultado, la luz de determinada frecuencia deberá difundirse en
el vacío como si lo hiciera a través de un "medio" que posee cierta
permeabilidad ![]() , la cual se determina por la misma luz difundida, o sea,
, la cual se determina por la misma luz difundida, o sea,
![]() .
.
Es sabido que la generalización de las ecuaciones de Maxwell mediante la
adición explícita de un miembro de masa en el lagrangiano de Maxwell conduce a
las ecuaciones de Prok en el espacio de Minkovski (según las concepciones
modernas). Las ondas electromagnéticas, que se desplazan en el medio, son
cambiadas por él y esta influencia se manifiesta mediante la generación de
fotones masivos [100]. Incluso si se supone la constancia de la velocidad de
fase, aparece una dependencia de la frecuencia (la dispersión en el vacío) de la
velocidad grupal de la luz: ![]() , aquí
, aquí ![]() es la masa de reposo de los fotones. En los
apéndices dados, empero, no se discutirán las cuestiones sobre la generación de
la masa y la teoría de la carga. El fin principal es reflejar ciertas cuestiones
físicas que tienen que ver con la velocidad misma de la luz.
es la masa de reposo de los fotones. En los
apéndices dados, empero, no se discutirán las cuestiones sobre la generación de
la masa y la teoría de la carga. El fin principal es reflejar ciertas cuestiones
físicas que tienen que ver con la velocidad misma de la luz.
Surgen inmediatamente las preguntas 1) ¿Cómo puede ser evaluada o medida la
dependencia de ![]() ? 2) ¿Por qué ella no ha sido observada hasta ahora? y 3) ¿Cuáles
pueden ser sus consecuencias?
? 2) ¿Por qué ella no ha sido observada hasta ahora? y 3) ¿Cuáles
pueden ser sus consecuencias?
Existen diferentes métodos para la medición de la velocidad de la luz, por
ejemplo: los métodos astronómicos, el método de las interrupciones, el método
del espejo giratorio, el método radiogeodésico, el método de las ondas
estacionarias (resonador), el método de las mediciones independientes de ![]() y
y ![]() . En la
actualidad el último de los métodos [59,67] es el más exacto; precísamente con
ayuda de éste método el Buró de Estándares mide la velocidad de la luz con una
exactitud de hasta el octavo signo. Pero en este camino existen dificultades
escenciales [7]. Además, hay que aclarar que el método dado está categóricamente
limitado: él puede estar enlazado o con la velocidad local de la luz (dentro del
aparato), o puede no tener absolutamente ninguna relación con la velocidad de la
luz, si es que la luz no es una onda pura. Por qué los otros métodos no son
adecuados (para la observación de la dependencia
. En la
actualidad el último de los métodos [59,67] es el más exacto; precísamente con
ayuda de éste método el Buró de Estándares mide la velocidad de la luz con una
exactitud de hasta el octavo signo. Pero en este camino existen dificultades
escenciales [7]. Además, hay que aclarar que el método dado está categóricamente
limitado: él puede estar enlazado o con la velocidad local de la luz (dentro del
aparato), o puede no tener absolutamente ninguna relación con la velocidad de la
luz, si es que la luz no es una onda pura. Por qué los otros métodos no son
adecuados (para la observación de la dependencia ![]() ) queda claro de los capítulos
anteriores y para una hipótesis particular esto, más adelante, quedará claro de
los presentes Apéndices.
) queda claro de los capítulos
anteriores y para una hipótesis particular esto, más adelante, quedará claro de
los presentes Apéndices.
Después investigaremos los métodos de la TER (olvidémonos por un rato que son
incorrectos, sino que dan solamente un efecto de visibilidad para dos
sistemas de referencia con una condición adicional: la condición de la
elección del método de sincronización de Einstein). Recordemos que al deducir
las consecuencias de la TER (por ejemplo, las leyes de transformación) se
utiliza el concepto de intervalo ![]() . Aquí es necesario hacer dos aclaraciones metódicas. En primer lugar
la igualdad de los intervalos
. Aquí es necesario hacer dos aclaraciones metódicas. En primer lugar
la igualdad de los intervalos ![]() no es más que una de las
hipótesis verosímiles ya que sólo el punto
no es más que una de las
hipótesis verosímiles ya que sólo el punto ![]() permanece como fidedigno (si
suponemos que
permanece como fidedigno (si
suponemos que ![]() ). Por ejemlo, se podrían igualar cualesquiera
). Por ejemlo, se podrían igualar cualesquiera ![]() -potencias
(
-potencias
(![]() es
natural):
es
natural): ![]() y obtener diferentes "Leyes físicas". O considerar que
y obtener diferentes "Leyes físicas". O considerar que
![]() ,
pero
,
pero ![]() , es decir
, es decir ![]() (la velocidad aparente del
movimiento mútuo es diferente para observadores distintos). Tal elección conduce
a la coincidencia del efecto relativista longitudinal de Doppler con la
expresión clásica. Semejantes sistemas exóticos pueden estar de acuerdo en el
mismo nivel que la TER (es decir, ¡sólo para dos objetos separados!), y sólo los
experimentos pueden mostrar cuál de las elecciones no es más que una invención
teórica. No discutiremos aquí toda estas hipótesis exóticas.
(la velocidad aparente del
movimiento mútuo es diferente para observadores distintos). Tal elección conduce
a la coincidencia del efecto relativista longitudinal de Doppler con la
expresión clásica. Semejantes sistemas exóticos pueden estar de acuerdo en el
mismo nivel que la TER (es decir, ¡sólo para dos objetos separados!), y sólo los
experimentos pueden mostrar cuál de las elecciones no es más que una invención
teórica. No discutiremos aquí toda estas hipótesis exóticas.
En segundo lugar, al utilizar el intervalo no se subraya el siguiente
momento: se utiliza una luz concreta que va de un punto a otro, es decir, en el
intervalo hay que sustituir la expresión ![]() . Pero en tal caso la proporcionalidad de los intervalos (de los libros
de texto) conduce a la relación indeterminada:
. Pero en tal caso la proporcionalidad de los intervalos (de los libros
de texto) conduce a la relación indeterminada:
yu no se puede fundamentar ni tan sólo la igualdad de los inatervalos.
Nuevamente surge la necesidad de referirse a los experimentos, ya que esta
relación está ligada a la ley, por ahora "desconocida", de Doppler. Así, las
construcciones teóricas que parten sólo de sus propios principios no son
unívocas. Puesto que la deducción convencional de la TER (el método) conduce a
ciertas consecuencias, supuestamente comprobables experimentalmente (¿por
ejemplo, con una cierta exactitud para la dinámica de partículas?), nos
apoyaremos en ella, pero la transformaremos con la consideración de la posible
dependencia ![]() .
.
Físicamente esto significa lo siguiente. El resultado visible de cierta
medición depende del procedimiento con que se midió y el resultado de cálculo
depende en particular del método de sincronización del tiempo para diferentes
sistemas. De acuerdo a la idea del presente apéndice no existe " una velocidad
única de transmisión de las interacciones electromagnéticas" (sino sólo ![]() ). Si
de acuerdo con Einstein se utiliza la luz de una determinada frecuencia
). Si
de acuerdo con Einstein se utiliza la luz de una determinada frecuencia ![]() para la
sincronización de los intervalos de tiempo, entonces el resultado de los
experimentos dependerá de
para la
sincronización de los intervalos de tiempo, entonces el resultado de los
experimentos dependerá de ![]() . Por ejemplo, sin en el sistema ocurre cierto proceso con
una frecuencia carcterística
. Por ejemplo, sin en el sistema ocurre cierto proceso con
una frecuencia carcterística ![]() , entonces es natural investigar dicho sistema
con ayuda de
, entonces es natural investigar dicho sistema
con ayuda de ![]() (precisamente de la manera en que se difunde la señal).
Si dos sistemas se mueven uno respecto al otro, entonces aparecerán dos
magnitudes en las fórmulas:
(precisamente de la manera en que se difunde la señal).
Si dos sistemas se mueven uno respecto al otro, entonces aparecerán dos
magnitudes en las fórmulas: ![]() y
y ![]() para cada sistema, ya que una
misma luz posee diferentes frecuencias en los sistemas que se mueven uno
respecto al otro. En este caso las magnitudes
para cada sistema, ya que una
misma luz posee diferentes frecuencias en los sistemas que se mueven uno
respecto al otro. En este caso las magnitudes ![]() y
y ![]() están relacionadas entre ellas a
consecuencia del efecto Doppler (ver más adelante). Es interesante notar la
siguiente circunstancia. Es el el sistema tienen lugar procesos con diferentes
características de frecuencia
están relacionadas entre ellas a
consecuencia del efecto Doppler (ver más adelante). Es interesante notar la
siguiente circunstancia. Es el el sistema tienen lugar procesos con diferentes
características de frecuencia ![]() , entonces, como consecuencia de las dependencias
, entonces, como consecuencia de las dependencias
![]() , los observadores que se mueven uno respecto al otroveran en un mismo
punto diferentes imágenes de los sucesos (efecto visible). En los siguientes
cálculos seguiremos la analogía con [4,17].
, los observadores que se mueven uno respecto al otroveran en un mismo
punto diferentes imágenes de los sucesos (efecto visible). En los siguientes
cálculos seguiremos la analogía con [4,17].
Sea ![]() la frecuencia de la señal que se transmite en el sistema. Colocando
la frecuencia de la señal que se transmite en el sistema. Colocando
![]() (en lugar de c) en la expresión del intervalo
(en lugar de c) en la expresión del intervalo ![]() para el propio
sistema y
para el propio
sistema y ![]() en
en ![]() para el sistema de observación, de
para el sistema de observación, de ![]() se sigue que el tiempo propio (
se sigue que el tiempo propio (![]() ) se puede determinar de la siguiente manera:
) se puede determinar de la siguiente manera:
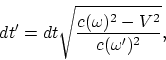 |
(A.1) |
y la fórmula para la longitud propia sigue siendo válida. Remarquemos nuevamente que estos son solamente "efectos de visibilidad". En cualquier expresión matemática los sumandos o los coeficientes se pueden trasladar de la parte izquierda a la derecha y viceversa (todas esas expresiones son equivalentes). Entonces, ¿cómo definir: el tiempo se aceleró para un observador o, por el contrario, se desaceleró en el otro (y la longitud aumentó o disminuyó)? Simple y sencillamente, si a usted le dijeran que su tiempo se desaceleró de una determinada manera respecto a un objeto y de otra manera distinta respecto a otros objetos, entonces usted sentiría la demencia de un número infinito de tales "testificaciones" inútiles. Pero cuando los relativistas le dicen a usted que todo está en órden, que simplemente "algo, para alguien, en algún lugar no muy lejano...", muchos se tranquilizan inmediatamente y continuan escuchando "los cuentos".
Para la deducción de las transformaciones de Lorenz utilicemos el giro en el
plano ![]() :
:
Entonces, utilizando ![]() las transformaciones de Lorenz
dan
las transformaciones de Lorenz
dan
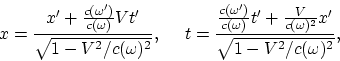 |
(A.2) |
donde ![]() es la velocidad del sistema. Escribiendo
es la velocidad del sistema. Escribiendo ![]() y
y ![]() en la expresión (A.2) y
encontrando
en la expresión (A.2) y
encontrando ![]() , obtenemos la transormación para la velocidad:
, obtenemos la transormación para la velocidad:
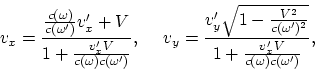
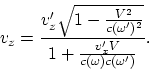 |
(A.3) |
Para el movimiento a lo largo del eje ![]() tenemos
tenemos
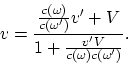 |
(A.4) |
Se observa que la velosidad máxima visible será ![]() , donde
, donde
![]() es
la frecuencia de la luz en el sistema propio. Notemos que todas las fórmulas
conducen a la ley correcta de la composición para el movimiento a lo largo de la
recta (las transformaciones del sistema
es
la frecuencia de la luz en el sistema propio. Notemos que todas las fórmulas
conducen a la ley correcta de la composición para el movimiento a lo largo de la
recta (las transformaciones del sistema ![]() al
al ![]() y de
y de ![]() a
a ![]() dan el mismo resultado que la transformación de
dan el mismo resultado que la transformación de
![]() a
a ![]() ). Recordemos
que, de acuerdo a la parte principal de este libro, las magnitudes
). Recordemos
que, de acuerdo a la parte principal de este libro, las magnitudes ![]() y
y ![]() en las
fórmulas (A.1), (A.2) no tienen un sentido físico independiente (son magnitudes
ficticias auxiliares). La fórmula (A.4), por analogía con la fórmula (1.5),
puede ser reescrita en la forma
en las
fórmulas (A.1), (A.2) no tienen un sentido físico independiente (son magnitudes
ficticias auxiliares). La fórmula (A.4), por analogía con la fórmula (1.5),
puede ser reescrita en la forma
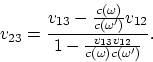 |
(A.5) |
En esta forma se aprecia mejor su sentido (efecto aparente). La fórmula
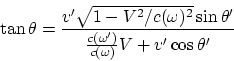 |
(A.6) |
describe el cambio de dirección de la velocidad. La expresión relativista
para la aberración de la luz se conserva (sustitución ![]() ). Por si
las dudas recordemos que la expresión relativista para la aberración estelar es
aproximada. Se conservan también las transformaciones de los vectores
4-dimensionales. De aquí se siguen las transformaciones del vector ondulatoria
4-dimensional
). Por si
las dudas recordemos que la expresión relativista para la aberración estelar es
aproximada. Se conservan también las transformaciones de los vectores
4-dimensionales. De aquí se siguen las transformaciones del vector ondulatoria
4-dimensional ![]() :
:
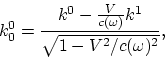
Obtenemos como resultado el efecto Doppler
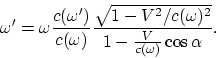 |
(A.7) |
Notemos que de aquí resulta la dependencia de la velocidad de la luz (![]() )
respecto al movimiento del sistema (a diferentes sistemas les corresponde una
frecuencia distinta
)
respecto al movimiento del sistema (a diferentes sistemas les corresponde una
frecuencia distinta ![]() ). Pero, como se mostrará en el siguente apéndice, este
efecto es despreciablemente pequeño para la región óptica. Los relativistas
aseguran que la expresión para efecto Doppler contiene una velocidad relativa.
Esto no es cierto. Supongamos que en un cierto punto sobre la Tierra ocurrió una
explosión y que una cierta línea irradió por un corto tiempo. Sea que un
receptor en Plutón registró la señal. ¿En qué momento hay que determinar esta
velocidad relativa mística? Pues en el momento del destello el receptor podría
no haber estado viendo hacia la Tierra; y en el momento de la recepción de la
señal la fuente ya no existe, y además la Tierra ya giró hacia el otro lado.
Incluso en ausencia de medio en vez de la velocidad relativa se obtendría una
diferencia de las velocidades absolutas en los momentos de emisión y recepción
de la señal (¡y esto no es lo mismo!). Pero qué es lo que tenemos en realidad,
eso lo deberá mostrar la experiencia.
). Pero, como se mostrará en el siguente apéndice, este
efecto es despreciablemente pequeño para la región óptica. Los relativistas
aseguran que la expresión para efecto Doppler contiene una velocidad relativa.
Esto no es cierto. Supongamos que en un cierto punto sobre la Tierra ocurrió una
explosión y que una cierta línea irradió por un corto tiempo. Sea que un
receptor en Plutón registró la señal. ¿En qué momento hay que determinar esta
velocidad relativa mística? Pues en el momento del destello el receptor podría
no haber estado viendo hacia la Tierra; y en el momento de la recepción de la
señal la fuente ya no existe, y además la Tierra ya giró hacia el otro lado.
Incluso en ausencia de medio en vez de la velocidad relativa se obtendría una
diferencia de las velocidades absolutas en los momentos de emisión y recepción
de la señal (¡y esto no es lo mismo!). Pero qué es lo que tenemos en realidad,
eso lo deberá mostrar la experiencia.
El vector de energía-impulso se transrforma como sigue:
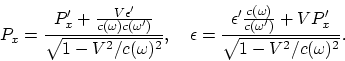 |
(A.8) |
Si seguimos la idea del presente apéndice, entonces deberá existir una analogía más estrecha entre la difusión de la luz en el vacío y en el medio.
(1) Diferentes paquetes de ondas se esparcen en el vacio de madera diferente.
(2) La dispersión de la luz en el vacío pone limitaciones categóricas al grado de paralelismo de los rayos.
(3) Tiene lugar la disipación de la luz en el vacío, o sea, la intensidad de la luz disminuye a medida que ella se difunde en el vacío.
(4) La luz " envejece", es decir, la frecuencia de la luz disminuye al difundirse en el vacío. Este fenómeno puede tener relación con la paradoja (de Olbers) de "¿por qué el cielo no arde?" y hacer su aportación al corrimiento hacia el rojo, es decir, es posible la correción de las concepciones sobre el desarrollo del Universo. Puesto que prácticamente se trata de la explicación alternativa del desfazamiento hacia el rojo entonces este efecto resulta ser muy pequeño y en el momento actual no es posible comprobarlo en las investigaciones de laboratorio: de todos modos el desfazamiento hacia el rojo de las líneas de los objetos cósmicos se detecta con métodos ópticos más exactos y dicho desfazamiento se vuelve notable sólo para objetos muy alejados, de tal modo que la distancia hasta ellos ya no se determina incluso mediante la base de la órbita terrestre (por triangulación); recordemos al respecto que la velocidad de la constante de Hubble ya fue corregida en un orden.
Al pasar a la electrodinámica cuántica es necesario realizar en todos los
cálculos la sustitución ![]() . Por ejemplo, esta dependencia
se manifiesta en la relación de las incertidumbres
. Por ejemplo, esta dependencia
se manifiesta en la relación de las incertidumbres
en la condición para la posibilidad de la descripción clásica
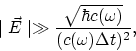
y en muchas otras fórmulas.
Cambian sustancialmente las formulas que describen la dependencia de ![]() . En
calidad de ejemplo analicemos la emisión y la absorsión de los fotones. Como
resultado aparece un nuevo coeficiente
. En
calidad de ejemplo analicemos la emisión y la absorsión de los fotones. Como
resultado aparece un nuevo coeficiente
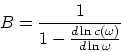
en las expresiones para el número de fotones ![]() de la
polarización dada:
de la
polarización dada:
y en la relación para las probabilidades (de absorsión, de emisión forzada y
espontánea) ![]() . La magnitud
. La magnitud ![]() aparece también en las
expresiones para los coeficientes de Einstein.
aparece también en las
expresiones para los coeficientes de Einstein.
Utilizando la sustitución ![]() para las oscilaciones propias
del campo, obtenemos la expresión para las comoponentes de Fourier del
propagador de fotones:
para las oscilaciones propias
del campo, obtenemos la expresión para las comoponentes de Fourier del
propagador de fotones:
En contrar ![]() sin una dependencia explícita
sin una dependencia explícita ![]() es imposible. Una forma
explícita de la dependencia de
es imposible. Una forma
explícita de la dependencia de ![]() es necesaria también para la obtención de las
expresiones finales para las diferentes secciones (de dispersión, de nacimiento
de pares, de desintegración...). En calidad de primera aproximación se puede
realizar la sustitución
es necesaria también para la obtención de las
expresiones finales para las diferentes secciones (de dispersión, de nacimiento
de pares, de desintegración...). En calidad de primera aproximación se puede
realizar la sustitución ![]() en las fórmulas conocidas.
en las fórmulas conocidas.