Acerca del posible mecanismo de la dependencia de la frecuencia

Partiendo del planteamiento semiclásico intentemos evaluar la dependencia $c(\omega)$ por analogía con la óptica. Prácticamente, esta es una de las posibles hipótesis sobre la transmisión de las oscilaciones electromagnéticas en el vacío. Describiremos al vacío como un cierto sistema, formado por pares virtuales (que no existen realmente) "partícula-antipartícula". En ausencia de partículas reales las partículas virtuales no se manifiestan de ninguna manera (no existen realmente) en el vacío. En la región de difusión de la luz aparecen oscilaciones de los pares virtuales. La difusión de la luz puede ser descrita como el proceso de interacción sucesiva entre los pares virtuales (exitación ondulatoria). El efecto más fuerte (las oscilaciones se exitan fácilmente) lo ejercen los pares más ligeros electrón-positrón. Por eso se considerarán sólo estos pares.

Puesto que las oscilaciones en el átomo o en el positrón son ejemplos de partículas reales, no pueden determinar la frecuencia propia de oscilación de los pares virtuales. Hay una sóla frecuencia que puede corresponder a un par virtual (que no existe sin exitación). La oscilación propia puede ser definida como la frecuencia que corresponde al nacimiento del par electrón-positrón $\omega_0=2m_ec^2/\hbar$, donde $m_e$ es la masa del electrón. Para tal descripción es razonable suponer que tanto el electrón como el positrón en el par virtual están localizados en un mismo punto (el par no existe realmente, es la aniquilación total). Utilizando el modelo clásico de los osciladores, se puede escribir la siguiente expresión para la velocidad de fase de la luz:

$$c(\omega) = {c_0\over\sqrt{\varepsilon}}, ~~~~~~ \sqrt{\varepsilon} = n - i\chi,$$ (B.1)

$$n^2 - \chi^2 = 1 + 4\pi {Nfe^2/m_e\over (\omega_0^2-\omega^2)^2 + 4\omega^2\gamma^2}(\omega_0^2-\omega^2),$$

$$n\chi = 4\pi {Nfe^2/m_e\over (\omega_0^2-\omega^2)^2 + 4\omega^2\gamma^2}\omega\gamma.$$

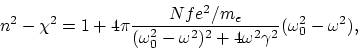
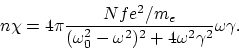
Resta determinar las magnitudes $c_0, \gamma$ y $Nf$. Al elegir la magnitud $\gamma$ no surge ninguna duda: ella se determina por la emisión de frenado (la única elección posible en el vacío):

$$\gamma = {e^2\omega^2\over 3m_ec^3}.$$

Aquí podemos investigas sólo aquellas regiones donde la electrodinámica clásica es interiormente consistente y aun no existen efectos cuánticos, es decir que $\omega\ll \omega_0/137$ y $\lambda \gg 3.7\times 10^{-11}$ cm $\gg R_0$, donde $R_0=e^2/(m_ec^2)$ es el radio del electrón. La magnitud $Nf$ representa tal número de pares virtuales por unidad de volúmen el cual es suficiente para proveer el proceso de transmisión de la luz. Prácticamente se habla de la determinación de las dimensiones del cuanto de luz y de la cantidad de partículas virtuales involucradas en él. Es evidente que el órden de las dimensiones longitudinales del cuanto $l\sim \lambda$. Para proveer la continuidad del cambio de los campos ${\bf E}$ y ${\bf H}$ se puede suponer que la "sustancia" del par virtual está " embadurnada" a lo largo de todo el cuanto (ver la Fig. B.1) y gira con una frecuencia $\omega$ sobre el eje local (perpendicular al plano del dibujo y que intersecta el eje $C$).

Figura B.1: La difusión de la luz como la polarización sucesiva del vacío.

La región ocupada por un par tiene las dimensiones: $(2R_0,2R_0,R_l)$, donde $R_l=\lambda/I$, $I$ es el número de pares "embadurnados". Puesto que la energía cinética media (la energía del campo magnético) es igual a la energía potencial media (la energía del campo eléctrico), el número $I$ se puede encontrar de la igualdad $2Ie^2/(2R_0)=\hbar\omega$. Entonces

$$R_l = {2\pi ce^2\over \hbar\omega^2R_0}, ~~~~~ Nf = {\hbar\omega^2\over 8\pi ce^2R_0}.$$

La expresión final aproximada para la velocidad adimesnional de fase de la luz tiene el aspecto:

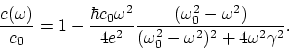$${c(\omega)\over c_{0}} = 1 - {\hbar c_{0}\omega^{2}\over 4e^... ...r (\omega_{0}^{2} - \omega^{2})^{2} + 4\omega^{2}\gamma^{2}}.$$ (B.2)

De aquí se ve que $c_0=c(0)$. La velocidad de fase disminuye con el crecimiento de la frecuencia.

Hagamos algunas evaluaciones (ver (B.2)). Para la región ultravioleta: $(\Delta c/c_0) \sim -0.5\times 10^{-6}$ (en la región visible el efecto es despreciablemente pequeño). Para $\omega\sim 10^{18}$ s$^{-1}$ el efecto $(\Delta c/c_0)\sim -1.4\times 10^{-5}$. La influencia del movimiento de la Tierra provoca a causa del efecto Doppler, incluso para la región ultravioleta, el efecto $(\Delta c/c_0)\sim -10^{-10}$ (despreciable); y en la frontera de la región de aplicabilidad de tal descripción ($\omega\sim \omega_0/137$) tenemos: $(\Delta c/c_0)\sim -3.6\times 10^{-7}$. Utilizando la expresión $c^2k^2=\omega^2\varepsilon$, para la velocidad grupal $U_g=(d\omega/dk)$ tenemos:

$$U_g{d(\omega\sqrt{\varepsilon})\over d\omega} = c_0.$$

La velocidad de grupo también decrece con el crecimiento de la frecuencia, coincidiendo prácticamente con la velocidad de fase. La mayor diferencia entre ellas se alcanza en la frontera de aplicabilidad de la descripción dada (para $\omega\sim \omega_0/137$) y cosntituye el 0.01 porciento (y respecto a $c_0$ del órden de $2\times 10^{-7}$). Notemos también que las dimensiones pequeñas del cuanto de luz utilizadas más arriba estan bastante fundamentadas (según las concepciones modernas). Tal objeto compacto interactuará como un todo y prácticamente de forma instantánea con cualquier objeto del micromundo, y no queda otra que postular prácticamente estas propiedades en la mecánica cuántica (por ejmplo, al explicar el fotoefecto o el efecto de Compton).

Las posibilidades experimentales actuales convencionales son insuficientes para la determinación de la dependencia de $\omega$ de la velocidad de la luz en la región visible (también para la influencia del movimiento de la Tierra). Aunasí presentemos algunas ideas generales relacionadas con los experimentos. Es necesario plantearse el fin mismo: observar la dependencia de $\omega$, $c(\omega)$. Las mediciones deben ser directas ya que cualquier consersión trae consigo determinadas concepciones teóricas sobre el proceso investigado. En particular, los experimentos deberán realizarse en el vacío puesto que el cálculo puramente teórico de la interacción de la luz con la materia no puede ser realizado con exactitud. En el caso general la interacción con la materia depende de la frecuencia de la luz $\omega$. En particular, loa espejos deberán reflejar diferentes ondas con diferentes frecuencias $\omega$ de diferentes maneras (además, la reflexión no es un proceso instantáneo). La conversión relacionada con la transformación de la luz no considera la posible dependencia de su velocidad de $\omega$. En el caso general, la interrupción del rayo de luz cambia el paquete de onda y, por consiguiente, su velocidad. Puesto que las partículas cargadas libres pueden influir sobre el efecto, es necesario evitar el blindaje metálico.

Para el método de las interrupciones es necesario al arranque simultáneo de los rayos con diferentes frecuencias y una adecuada exactitud para la determinación de los intervalos de tiempo cuando el frente de onda haya recorrido determinada distancia. O, alternativamente, se puede excluir la línea espectral de la mezcla de dos líneas espectrales (laseres) con ayuda de la interrupción. Puesto que la reflexión no es un procéso instantáneo y depende de la frecuencia de la luz, la práctica estandard del aumento del recorrido con ayuda de espejos no sirve en absoluto, o bién el número de reflejos para cada rayo de luz (¡para cada frecuencia diferente!) debe ser igual. La última aclaración es aplicapble también al método interferométrico. Dividimos el rayo ($\omega_1$) en dos rayos. El primer rayo se transforma (en $\omega_2$) al inicio del recorrido $L$ y el segundo, al final de $L$. El recorrido $L$ puede cambiar. Si existe la dependencia $c(\omega)$, entonces la imágen de interferencia deberá cambiar con el cambio de $L$. Sin embargo, hay dificultades técnicas para medir $L$ sin perturbaciones.

Las investigaciones astronómicas para un espectro bastante amplio $\omega_i$ pueden ayudar a observar la dependencia $c(\omega)$. Se puede observar desde un satélite la aparición y desaparición no sincronizada de las características espectrales de las formas en los sistemas dobles durante el eclipse total. Empero, no existe la seguridad total (para grandes distancias) de que la luz efectivamente pasa a través del vacío (sin gas, plasma, polvo...). Es necesario un análisis matemático adicional $c(\omega_i)$ para $\omega_i$ para encontrar la dependencia $c(\omega)$.

El mayor interés lo representa la comparación de $c(\omega)$ para la región visual y para la de rayos $X$ y $\gamma$. Hasta donde sabemos, no hay datos experimentales para estas regiones. No obstante, para los experimentos con rayos $\gamma$ existe una serie de dificultades (ver [7,59,67] para el método más exacto de las mediciones independientes directas $\lambda$ y $\nu$, con la consideración del modelo ondulatorio de la luz), sí y no hay una certeza completa acerca de la naturaleza puramente ondular de la luz.

La pregunta más general del presente apéndice suena así: ¿permanecen inmutables las propiedades del vacío al introducir partículas (fotones) en él o no? Si las propiedades del vacío cambian, entonces deberá existir el efecto contrario (el principio de interacción) sobre el proceso de difusión de las partículas (la luz). La dependencia $c(\omega)$ es una cierta manifestación de dicho principio.

De esta manera, en los apendices se dedujeron las fórmulas correspondientes para las consecuencias de la dependencia $c(\omega)$ relacionadas con la TER, la electrodinámica cuántica, la óptica, etc. Para la observación del hecho mismo de la dependencia $c(\omega)$ son necesarias investigaciones orientadas hacia este fin. El máximo efecto deberá observarse en la región de altas frecuencias. Aunque las dificultades experimentales son serias, los posibles resultados son escencialmente importantes e interesantes.

Aquí se discutió uno de los posibles mecanismos que llevan a la dependencia $c(\omega)$ para el modelo ondulatorio de la luz, pero recordemos que no existen experimentos críticos que refuten la ley clásica de la suma de velocidades incluso para el modelo corpuscular de la luz, sin hablar ya del modelo ondulatorio. La cuestión está en que para la luz las siguientes tres dependencias están unívocamente correlacionadas en el modelo ondulatorio de la luz: la dependencia $c(\omega)$, la ley de Doppler y la ley de la suma de las velocidades. Sólo el conocimiento de dos de estas dependencias define unívocamente a la tercera. Para el modelo ondulatorio el proceso de difusión de las oscilaciones electromagnéticas (la luz) en el vacío puede ser descrito como la aparición sucesiva de oscilaciones de partículas virtuales (pares), la cual es provocada por la misma luz difundida. (A decir verdad, para el modelo analizado en este apéndice surge la pregunta sobre las diferencias en las propiedades de la luz, que aparecen durante la aniquilación de partículas más pesadas, y sobre el papel de otros pares virtuales o sobre " elementalidad" de las partículas elemetales).