Algunas soluciones y consecuencias relativistas

Estudiemos la paradoja de la transformación de las fuerzas. Supongamos que tenemos dos cargas en reposo de signo diferente $e_1$ y $e_2$ divididas por dos planos paralelos, los cuales se encuentran a una distancia $L$ uno del otro (Fig. 4.4).

Figura 4.4: La paradoja de la transformación de las fuerzas.

A consecuencia de la atracción de una hacia la otra, las cargas se encuentran a una distancia mínima $L$ una de la otra. (Ellas se encuentran en un equilibrio indiferente con relación al sistema de los planos.) Pongamos una marca en el plano bajo cada carga o coloquemos observadores al lado. Observaremos ahora este sistema de cargas desde un cohete relativista que se mueve a una velocidad ${\bf v}$. Sea que $\theta$ es el ángulo entre los vectores ${\bf v}$ y ${\bf L}$. Al determinar las fuerzas electromagneticas que actúan entre estas cargas en el sistema de referencia del cohete [17], nos interesaremos por las componentes tangenciales de las fuerzas, o sea, por las componentes de las fuerzas a lo largo de los planos. Sobre la carga $e_1$ actúa la fuerza

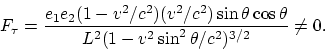$$F_{\tau} = {e_1e_2(1-v^2/c^2)(v^2/c^2)\sin\theta\cos\theta\over L^2(1-v^2\sin^2\theta/c^2)^{3/2}}\ne 0.$$ (4.1)

Por consiguiente, las cargas tienden a moverse desde su posición original. Sea que las bolas tienen enormes carga, $L$ es pequeña ($L\rightarrow 0$) y $v$ es grande ($v\rightarrow c$). Supongamos que los observadores sostienen las esferas con hilos delgados. ¿Se romperán estos? La respuesta depende del sistema de observación. ¿Cuál de los observadores tiene la razón? De este modo, tenemos la contradicción habitual de la TER.

Analicemos ahora algunos problemas particulares. La descripción del movimiento de la partícula cargada $e$ de masa $m_0$ en el campo eléctrico constante y homogéneo $E_x=E$ (ver. [34]) es metódicamente paradójico. Efectivamente, en la física clásica la trayectoria para $v_y=v_0$ es la parábola

$$x = eEy^2/(2m_0v_0^2),$$

pero en la TER es un línea en cadena

$$x = {m_0c^2\over eE}\biggl ( \cosh\biggl [ {eEy\over m_0v_0c}\biggr ] - 1\biggr ).$$

Pero para grandes y la trayectoria relativista es ceracana a la exponencial, o sea, es más inclinada que la parábola. ¿Y qué hacer con la idea sobre el aumento de la inercia (de la masa) al aumentar la velocidad? Incluso si consideramos que, a pesar de la gran inclinación, la partícula se mueve más lentamente pos la trayectoria, entonces ¿a cuenta de que fuerzas se desaceleró en el eje $y$? Ya que la fuerza $F_y=0$ tampoco aparecerá en la TER: $F'_y=0$. Y el valor de la velocidad inicial $v_y=v_0$ puede ser no-relativista (y permanecerá como tal).

Resulta extraño el balance de la energía para el cohete relativista [33]:

$$m\cosh\theta + M_2\cosh(d\theta) = M_1.$$

A una gran velocidad de expulsión ($\theta=\tanh(v/c)$) para los valores finales de las masas inicial $M_1$ y final $M_2$ se deberá cumplir la condición: la masa de una expulsión individual $m\rightarrow 0$ (para que no se contradiga la TER). Pero este valor se determina sólo por la construcción técnica del cohete: no hay limitaciónes categóricas.

Una de las deducciones de Einstein de la relación $E=mc^2$ no está lo suficientemente fundamentada. En esta deducción el proceso de absorción por el cuerpo de dos impulsos luminosos simétricos se analiza desde el punto de vista de dos observadores que se mueven uno respecto al otro. El primer observador está en reposo respecto al cuerpo, el segundo se mueve de manera perpendicular a la luz (Fig. 4.5).

Figura 4.5: Para la deducción de la fórmula $E=mc^2$.

En la TER resulta que la luz debe saber de antemano acerca del movimiento del observador precisamente a la velocidad $v$ y obtener el impulso de tal manera que en este segundo sistema la velocidad del cuerpo no cambie sino que cambie solamente su masa. ¿Qué hacemos entonces con los experimentos de Lebediev sobre la presión de la luz (y para las concepciones actuales aceptadas generalmente), cuando al transmitir un impulso mediante la luz cambió precisamente la velocidad observada del objeto? ¿Y qué pasará con el impulso si tenemos superficies irregulares (sesgadas) absolutamente absorbentes? De los dibujos presentados tampoco está claro si tenemos que ver con una luz transversal real (con el modelo aceptado en la actualidad, inclusive en la TER) o con una luz transverso-longitudinal mística (para la salvación de la TER).

Es bastante extraña en la versión actual de la TER la diferencia de la masa de la emisión general en dependencia del impulso del sistema:

$$m = \sqrt{{(E_1+E_2)^2\over c^4} -{({\bf P}_1+{\bf P}_2)^2\over c^2}}.$$ (4.2)

¿Y si cambiamos el impulso (la dirección) de fotones separados mediante espejos? Aquí determinaremos además el centro de gravitación del sistema. ¿Dónde estará localizado y cuál será la estructura del campo en las cercanías? ¿Acaso este centro saltará, desaparecerá y aparecerá nuevamente? Utilicemos la fórmula expuesta de la TER (4.2) para la determinación de la masa de la emisión general de dos fotones que se separan en un ángulo arbitrario y analicemos la emisión que se dispersa desde un mismo centro (Fig. 4.6).

Figura 4.6: La masa de la combinación de fotones.

Entonces para la dependencia de la agrupación por pares de los fotones se puede obtener una diferente masa general de todo el sistema (¿habrá también que introducir artificialmente masas negativas para la " explicación" de todas las posibles variaciones de la masa?). Pero en la TGR hay que considerar la prehistoria del nacimiento de la radiación para determinar la localización del centro de gravitación de dicha radiación y considerar toda la estructura espacio-temporal desconocida del campo electromagnético para la descripción correcta de otro fenómeno: el de la gravitación. ¡Es infinitamente complicado!