Las ecuaciones de Maxwell

La siguiente nota breve se refiere a las ecuaciones de Maxwell (en su forma actual, comúnmente aceptada). Recordemos que ellas se obtuvieron mediante la generalización fenomenológica de los hechos experimentales para velocidades pequeñas (se tomó la analogía con la hidrodinámica). Por lo tanto no hay que esperar que hayan sido adivinadas en su forma final. Las ecuaciones de Maxwell (o la ecuación de onda) determina la velocidad de fase, mientras que en la teoría de la relatividad "se pretende" la velocidad máxima de las señales (velocidad de grupo). Prácticamente, tenemos siempre que ver con una luz concreta, por eso este hecho debe ser marcado con un cierto índice: en vez de $c$ hay que escribir la dependencia paramétrica $c(\omega)$ y la ecuación de onda será la ecuación para los ármonicos de Fourier. Puesto que los apologetas contemporáneos del relativismo niegan la evidencia y la necesidad básica de los modelos del medio de difusión de la luz, entonces deja de ser unívoco el camino de la generalización de las ecuaciones de Maxwell incluso para el "vacío absoluto" en el caso de la luz no-monocromática, sin hablar ya del paso hacia los medios no-lineales reales (que incluyen las propiedades del "vacío intermolecular", los mecanísmos de absorción y reemisión de la luz por las moléculas, etc.): fuera de los principios físicos y partiendo sólo de concepciones matemáticas puras se pueden realizar cuantas generalizaciones semejantes se desee y todas tendrán la misma validez. La exigencia de la invariabilidad de las ecuaciones de Maxwell respecto a las transformaciones de las coordenadas y del tiempo es bastante escurridiza, ya que los campos y las ecuaciones para ellos se pueden introducir de muchas maneras, tan sólo deberán las acciónes medidas de estos campos coorresponder a magnitudes realmente observadas en los experimentos. Así, por ejemplo, en [81] se muestra que existen transformaciones no locales de los campos, las cuales conservan las ecuaciones de Maxwell con un tiempo invariable. En [14] se muestra que se pueden introducir transformaciones no locales y no lineales para que durante determinadas transformaciones de los campos las ecuaciones del campo sean invariantes respecto a las transformaciones de Galileo.

Demostremos la contradicción metódica de las transformaciones para los campos universalmente aceptadas. Supongamos que se tienen dos alambres paralelos infinitos sin carga. Sea que en ambos alambres los electrones se mueven hacia una misma dirección a una velocidad constante respecto a la armadura cargada positivamente, es decir, tenemos iguales densidades de corriente ${\bf j}$. Entonces, para el caso clásico, en la expresión para el campo la magnitud

$$jdV = en(v_{+} - v_{-})dV$$

es invariante, o sea que el campo $H_{\perp}$ y la acción de este campo no dependen de la velocidad de movimiento del sistema. Para la consideración relativista (puesto que ${\bf E}=0$) tenemos

$$H_{\perp} = {H_{\perp}^0\over \sqrt{1-v^2/c^2}},$$

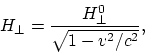
o sea que el campo depende de la velocidad de movimiento del obsrvador. Sin embargo, los siguientes dos casos son evidentemente equitativos:
(1) el sistema con la velocidad ${\bf v}_{obs}=0$, o sea el observador, está en reposo respecto a la armadura mientras que los electrones se mueven a la velocidad ${\bf v}$, y
(2) el sistema se mueve con la velocidad ${\bf v}_{obs}={\bf v}$, o sea el observador, está en reposo respecto a los electrones mientras que la armadura (los iones positivos) se mueven hacia la dirección contraria a una velocidad $-{\bf v}$ (esa misma corriente). La fórmula relativista da para estos casos diferentes valores para $H_{\perp}$ (y para la acción de los campos), lo cual es absurdo. Además resulta completamente contradictoria en la TER la descripción de los pasos de un sistema inercial a otro para el caso tridimensional con corrientes no neutrales (por ejemplo, con haces de partículas cargadas).

Analicemos ahora la pregunta "fundamental" sobre la invariancia de las ecuaciones de Maxwell, la cual ha sido ampliamente promovida en la TER. La invariancia de las ecuaciones de Maxwell respecto a las transformaciones de Lorenz no significa absolutamente nada para otros fenómenos. En primer lugar, las de Maxwell son ecuaciones para los campos en el espacio vacío. En tal espacio podemos recortar la mitad del segmento y duplicarla, obtendremos nuevamente tal segmento. Por eso en el espacio vacío matemático se puede utilizar cualquier sistema de referencia, cualquier geometría y coeficientes de transformación no contradictorios. Esto puede determinarse sólo por la comodidad de la descripción matemática. Sin embargo, no podemos simplemente recortar cualquier organismo vivo y duplicarlo bajo el microscopio: el organísmo morirá. La existencia en el espacio de cuerpos y campos reales da puntos de referencia naturales, escalas carácterísticas e correlaciones entre los objetos. Todo esto determina las diferencias entre el espacio real físico y el espacio vacío matemático. En segundo lugar, la propiedad de algunas interacciones de transmitirse en el vacío a la velocidad de la luz no determina la velocidad de transmisión de las interacciones en el medio. A pesar del enorme papel de de las interacciones electromagnéticas, las perturbaciones en los medios se transmiten con la velocidad del sonido. Mediante la sola constante $c$, relacionada con el vacío, no se pueden determinar (para nuestro mundo " electromagnético") la velocidades de la luz y del sonido en los gases, líquidos y sólidos. No está claro como pudo surgir en el vacío istrópico la anisotropía de los cuerpos sólidos reales. Todas estas y muchas más propiedades se sales ‡n de los límites de aplicación de las leyes de Maxwell en el vacío (la TER sugiere la clonación de las propiedades del vacío para todas las propiedades de los cuerpos materiales y de los medios). Luego, ajustar las propiedades de todo el Universo para que encajen en la invariancia de estas ecuaciones es una pretención muy elevada de la TER. En tercer lugar, la partición de un campo único en su acción en sus partes eléctrica y magnética es bastante convencional y en gran medida arbitrario. Por eso la invariancia de estas partes separadas artificialmente no puede tener un significado decisivo. La existencia de los coeficientes $\rho, \varepsilon, \mu$ (que dependen de las coordenadas, del tiempo, de las propiedades de la luz, etc.) para las ecuaciones de Maxwell en el medio hace estas ecuaciones no invariantes respecto a las trasnformaciones de Lorenz (o bien hay que cancelar nuevamente la objetividad de las características del medio).