Aclaraciones adicionales

En la física clásica todos los conceptos tienen un sentido bien determinado y no hay que cambiarlos por sucedáneos. Que los relativistas les inventen otros nombres a sus nuevos conceptos (más ciertamente a sus combinaciones de símbolos). La definición relativista del centro de inercia [17]:

$${\bf R} = {\sum E{\bf r}\over\sum E}$$

no tiene sentido físico ya que en la TER el centro de inercia de un mismo sistema de partículas en movimiento resulta diferente en distintos sistemas de referencia. Esto significa que no realiza su finalidad funcional de centro de equilibrio. Supongamos que tenemos una caja plana masiva en la cual se mueven unas bolitas masivas. Sea que en el caso clásico el centro de inercia de todo el sistema coincide siempre con el centro de la caja durante el proceso de movimiento y choque de las bolas. Entonces en el caso clásico lo podemos equilibrar (por ejemplo, en el campo de gravedad de la Tierra o en otro campo) sobre un soporte de sección pequeña (Fig. 4.3) y el equilibrio se conservará.

Figura 4.3: El centro de inercia del sistema y el equilibrio.

En la TER, al contrario, si nosotros vemos este sistema desde un cohete relativista que se mueve rapidamente entonces el centro de inercia puede resultar fuera del soporte y el equilibrio se romperá. Una objetividad admirable la de la TER: para no romper el equilibrio del plasma en la síntesis termonuclear controlada, se les pide a los cohetes relativistas no asomarse ni volar sobre el experimento.

El enlace relativista entre la masa y la energía no refleja en realidad nada escencial. En efecto, la expresón clásica para la energía cinética

$$E = {mv^2\over 2}$$

y la expresión relativista

$$E = mc^2\biggl ( {1\over \sqrt{1-v^2/c^2}} - 1\biggr )$$

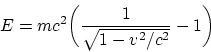
no se distinguen (cualitativamente) en nada. Ambas son magnitudes de cálculo. El intento de medir estas magnitudes (es decir, la graduación del aparato) depende de la interpretación de la teoría, puesto que estas magnitudes no pueden determinarse comparandolas con el prototipo. Puesto que en la expresión relativista de la energía

$$E = {mc^2\over \sqrt{1-v^2/c^2}}$$

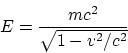
además de la masa entran otras magnitudes, entonces para cualesquiera correlaciones posibles la masa y la energía permanecen como magnitudes diferentes (no equivalentes, independientes). Incluso para la llamada "energía de reposo" $E=mc^2$ tampoco se puede hablar de las transformaciones mutuas entre la masa y la energía. La cuestión está en que durante la aniquilación (la única candidata a un proceso semejante) se forman fotones para los cuales la "masa en movimiento" se postula en la TER mediante esa misma fórmula. Por lo tanto, también en este caso se trata sólo de de las trasformaciones mútuas de las partículas. Sin hablar ya de que la " energía en reposo" es sólo una hipótesis de la TER, puesto que la teoría conduce también a esa misma constante indeterminada que en la física clásica.

Prestemos atención también a la no invariancia de la fórmula $E=mc^2$ dentro del marco de la TER: la masa es invariante, la velocidad de la luz también. Pero la energía es en si misma un vector 4-dimensional. Si se intenta agregar a la energía de un cuerpo la energía cinética de sus moléculas, que se mueven a diferentes velocidades ${\bf v}_i$, entonces al pasar a un sistema en movimiento estas velocidades se sumaran de diferentes maneras con la velocidad del cuerpo como un todo. Como resultado la correlación se rompe y en el nuevo sistema esta fórmula resulta ser simplemente la definición relativista de una cierta "letra $E$".

La TER intenta "luchar contra molinos de viento" desde posiciones categóricas: por ejemplo, con el concepto de sólido absoluto. Empero, en la física clásica nadie le asigna un sentido literal a la abstracción de sólido absoluto. Es evidente para todos que no existen cuerpos absolutamente sólidos incluso para velocidades completamente no relativistas (notemos el papel de las aceleraciones, más exactamente de las fuerzas, recordando los choques comunes de los automóviles en las calles). Simplemente durante la descripción de ciertos movimientos la influencia de la deformación es bastante despreciable o no es escencial para el fenómeno estudiado y entonces, sólo para la simplificación de los cálculos matemáticos, se utiliza la abstracción de sólido absoluto. La TER intenta categóricamente considerar que las partículas elementales son puntuales [17] e inmediatamente se topa con otro problema escencial: el de la singularidad de una serie de magnitudes.

Pasemos ahora directamente a las aclaraciones sobre la dinámica relativista (la teoría de los choques y las leyes del movimiento de las partículas cargadas).