El principio de Mach

El principio de Mach sobre la condicionalidad de la masa inerte y sobre el carácter absoluto de la aceleración a causa de la acción de las estrellas lejanas también es dudoso ya que explica las propiedades internas de un cuerpo a través de las propiedades de otros cuerpos. Claro que la idea en sí es hermosa. Si concideramos que todo en el mundo está interelacionado y existe una cierta ecuación ideal total de estado, entonces cualquier propiedad de los cuerpos deberia determinarse por la influencia del resto del Universo. Empero, cada una de las parículas debería considerarse como individual. Este camino es más fácil para la ciencia, que va de un menor a un mayor conocimiento, ya que no se puede abarcar lo que es "inabarcable". Prácticamente, si consideramos la distribución heterogénea de la masa (en objetos compactos) y las diferentes magnitudes de las fuerzas de atracción de los objetos cercanos y lejanos, entonces obtendríamos u "jaloneo" total en vez de un giro uniforme o de un movimiento uniforme por inercia.

Categóricamente el principio de Mach no puede ser comprobado: tanto la expulsión de todos los cuerpos del Universo como la tendencia artificial hacia cero de la constante gravitacional, una abstracción que no tiene nada que ver con la realidad. Sin embargo, experimentalmente se puede evaluar el efecto de las " estrellas lejanas" si se considera que la masa del Universo está concentrada principalmente en objetos compactos. La fuerza de atracción de una estrella de masa semejante a la del Sol $M\sim 2\cdot 10^{30}$ kilogramos, la cual se encuentra a una distancia de 1 año luz $\sim 9\cdot 10^{15}$ metros es equivalente a la acción de un peso cuya masa es de sólo $m_0\sim 25$ gramos y que se encuentra a 1 metro de distancia. Utilicemos por ahora la dudosa teoría de la Gran explosión y consideremos que el tiempo de existencia del Universo es de $\sim 2\cdot 10^{10}$ años. Incluso si las estrellas se alejaran volando a la velocidad de la luz, el Universo tendría unas dimensiones de $\sim 2\cdot 10^{10}$ años luz. Consideramos que la distancia promedio entre las estrellas más cercanas es de 1 año luz. Aumentamos intencionalmente todas las magnitudes, por ejemplo, la masa del Universo y su densidad $\rho\sim 10^{33}/10^{54}\sim 10{-21}$ g/cm$^3$. Consideremos ahora que al alejarse los cuerpos uno del otro al doble de distancia, la fuerza disminuye cuatro veces y así sucesivamente. Intentemos imitar la fuerza de interacción de todo el Universo en una cierta dirección. Incluso si consideramos la distancia media entre los cuerpos más cercanos igual a 1 año luz, a una distancia de un metro es necesario colocar un masa en gramos (sumamos hasta $2\cdot 10^{10}$)

$$M_0\sim 25(1+1/4+1/9+\cdots) = 25\sum 1/n^2\sim 25\pi^2/6 < 50.$$

Prácticamente el coeficiente $\pi/6$ expresa cierto aumento efectivo de la densidad sobre la línea de observación. Para la initación de "todo el Universo" se puede tomar una esfera metálica gruesa de radio exterior igual a un metro y se puede hacer el grosor variable en la dirección hacia el centro (para la imitación de las heterogeneidades se puede incluso hacer una estructura acicular cerca del radio interior).

Supongamos que el grosor de la esfera sólida es de $0,6$ metros, es decir, del centro hasta $0,4$ metros tenemos el nicho y de ahí en adelante hasta 1 metro tenemos el metal. Entonces a la masa $M_0$ con una densidad de $\sim 8,3$ g/cm$^3$ le corresponderá a una columna cilíndrica de radio $0,35$ cm. En la realidad debemos considerar la influencia de las estrellas en el cono y no sólo en el cilindro. Aunque también tenemos un cono metálico esférico, de cualquier modo evaluemos el órden de la magnitud. Descompongamos el cono en capas cilíndricas, las cuales aparecen a medida que se incorporan nuevas capas de estrellas (Fig. 2.9).

Figura 2.9: El principio de Mach y la influencia del Universo.

Cada nueva capa será mayor que la anterior en $6$ estrellas. La distancia desde el centro hasta la frontera más cercana de cada capa de estrellas se puede encontrar de la analogía con los triángulos: $R_i/1=i/r$. Entonces tenemos $R'_i=\sqrt{i^2(1+r^2)}/r$. Luego tenemos que la correción para la masa $M_0$ (sumamos hasta $2\cdot 10^{10}$) se encuentra como

$$m_0(1+{1\over 4}+\cdots )\biggl ( 1 + \sum_i {6\over {R'}_i^2}\biggr ) < M_0\biggl ( 1+ 6r^2 \sum_i {1\over i}\biggr )$$

$$\sim M_0\biggl ( 1 + 6 \cdot 10^{-5} \log{(2 \cdot 10^{10})}\biggr ) \sim M_0(1+0,02).$$

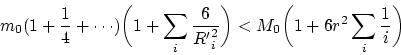
De esta manera, nuestra construcción alcanza con creces para la consideración de la acción de "todo el Universo". Por supuesto que si el Universo es infinito, la serie armónica obtenida divergerá y la construcción será no adecuada. Pero esto contradice tanto a la TGR como a los puntos de vista actuales y a los datos observacionales.

Coloquemos ahora bolitas en resotes dentro de la esfera. Para evitar efectos indirectos se puede succionar el aire de dentro de la construcción y aislar adicionalmente las bolitas de la esfera mediante un contenedor delgado. Si empezamos a girar la esfera entonces, de acuerdo al principio de Mach, deberá aparecer una fuerza centrífuga y las bolitas se separarán. aquí la fuerca centrífuga deberá ser la misma que si giraran las propias bolitas. Parece bastabte obvio que esto no es posible ya que tal efecto se habría descubierto hace mucho. De esta manera regresamos a los conceptos absolutos de aceleración, masa, espacio y tiempo determinados ya por Newton. Pero el experimento descrito podría resultar útil para la determinación de las correciones a la ley estática de Newton. Aquí las bolitas deberán tener bastante libertad para moverse y girar ya que no se conoce de antemano la dirección de la acción de las fuerzas correctoras y de los momentos de las fuerzas.