El principio de equivalencia

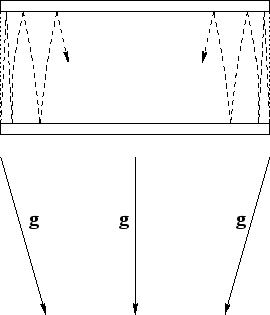
Pasemos ahora al siguiente concepto importante de la TGR: la equivalencia del campo gravitacional de un cierto sistema no inercial. A diferencia de cualquier campo inercial el campo gravitacional posee una propuedad única: todos los objetos en movimiento se inclinan hacia un centro. Si se emiten dos rayos permendicularmente entre dos espejos idelamente paralelos, entonces en un sistema inercial ellos se moveran paralelamente uno al otro infinitamente entre los espejos. Una sistuación análoga se tendrá bajo el efecto de la aceleración en un sistema no inercial si los espejos están orientados perpendicularmente respecto a la dirección de la aceleración. En el campo gravitacional será al contrario, con una orientación análoga de los espejos, los rayos empezarán a acercarse (Fig. 2.5).

Figura 2.5: El acercamiento de los rayos paralelos en el campo gravitacional.

Y si se va a medir algún efecto durante el tiempo de observación entonces, a consecuencia del gran valor de la velocidad de la luz, precisamente la presencia del campo gravitacional (y no la no-inercialidad) será también identificada. Es evidente que no hay que considerar la curvatura de los espejos ya que, además de las fuerzas gravitacionales, existen otras fuerzas que pueden mantener la configuración mútua de los espejos. La diferencia entre la simetría esférica y la plana puede ser establecida también para campos gravitacionales débiles. La conclusión de la TGR acerca de la posible exclusión del campo gravitacional para un cierto sistema inercial durante todo el transcurso del tiempo de observación es, en el caso general, falsa.

El principio de equivalencia de la gravitación y de la aceleración puede tener relación sólo respecto a un punto del espacio, es decir, es irreal: esto, por ejemplo, ya condujo al calculo erróneo de la inclinación de un rayo de luz en el campo de la gravedad (sólo después Einstein corrigió el coeficiente y lo aumentó dos veces). El principio de equivalencia de las masas inerte y pesada puede ser estrictamente formulado en la TGR también sólo para un cuerpo separado (puesto que la TGR incluye el enlace mutuo entre el espacio-tiempo y todos los cuerpos, entonces él no es real en la TGR). Por eso físicamente la TGR no puede tener un paso límite a ninguna de las teorías no relativistas (sino sólo formalmente de modo matemático). Todas las transformaciones lineales de la TER y la TGR se refieren al espacio vacío ya que los cuerpos reales (incluso en calidad de puntos de referencia) introducen la no-linealidad en las propiedades del espacio. Por eso la diferencia de los fenómenos al pasar a otro sistema de coordenadas se deberá estudiar estrictamente en un mismo punto del espacio y del tiempo. ¿Pero cómo colcar en un mismo punto a dos diferentes observadores? Por lo tanto, todas las tareas de la TER y de la TGR pueden tener sólo un carácter de modelo aproximado (sin globalización).

No hay nada asombroso en el hecho de que una misma magnitud - la masa - pueda participar en diferentes fenómenos: como medida de la inercia en la interacción de cualesquiera fuerzas, incluyendo las gravitacionales, y como masa atractiva (por ejemplo, la carga en movimiento crea un campo eléctrico y uno magnético). La cuestión respecto a la igualdad exacta entre la masa inercial i la gravitacional es completamente inventada ya que esta igualdad depende de la elección del valor numérico de la constante gravitacional $\gamma$. Por ejemplo, en el caso de la proporcionalidad $m_g=\alpha m_{in}$ todas las leyes serán las mismas pero con otra definición de la constante gravitacional $\gamma'=\alpha^2\gamma$. No hay que buscar aquí ningún misticismo ni crear imágenes del espacio curvado. La sustitución de una misma magnitud tanto para la masa gravitacional como para la inercial se lleva a cabo no sólo en la TGR, sino también en la teoría de la gravitación de Newton. Simplemente esto es un hecho experimental (más bien, la elección más simple de la magnitud $\gamma$).

Cuando hablan de que la forma de la ecuación depende de las propiedades del espacio-tiempo [37], en ello hay una cierta especulación. Se tiene la sensación de que nosotros, de alguna manera, podemos cambiar ese mismo espacio-tiempo para comprobar la dependencia dada. En realidad tenemos un Universo en número singular. El intento de la TGR de complicar cualquier fenómeno particular (local) agregándole la complejidad de todo el Universo no es positivo para la ciencia. Otra cosa es la elección de las coordenadas locales para la descripción matemática de un fenómeno local (en este caso las simetrías concretas del fenómeno simplifican la descripción), y nuevamente el globalismo no tiene nada que ver aquí.

El uso de sistemas no inerciales en la TGR es internamente contradictorio. En efecto, en un sistema en rotación los objetos bastante alejados se moverán a una velocidad mayor a la de la luz, pero la TER y la TGR afirman que las velocidades visibles deberán ser menores que $c$. Sin embargo, es un hecho experimental: la fotografía del cielo desde la Tierra en rotación muestra que se observa un giro visible de cuerpo sólido (clásico). El uso de un sistema que gira (por ejemplo, la Tierra) no contradice a la física clásica para cualquier distancia del objeto desde el centro, mientras que en la TGR el valor de la componente $g_{00}$ se vuelve negativo, lo cual no está permitido en dicha teoría. ¿Que hacer entonces con las observaciones astronómicas?