La paradoja de la cruz

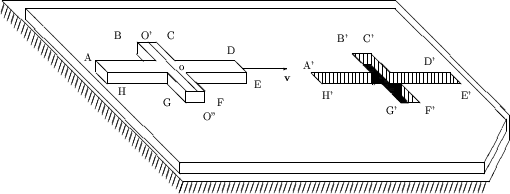
Supongamos que en un plano firme yace una placa delgada de gran tamaño y de la cual se ha recortado una pequeña cruz (Fig. 1.15).

Figura 1.15: La paradoja de la cruz.

Supongamos que la longitud de la cruz es mucho mayor que la anchura del brazo $\vert AD\vert\gg \vert BC\vert$. Supongamos que la cruz se desliza horizontalmente por la placa de tal manera que en la física clásica ocupe su nicho (por ejemplo, cayó en él a causa de la fuerza de gravedad). Elijamos una velocidad relativa de movimiento ${\bf v}$ de tal modo que la longitud, de acuerdo a las fórmulas relativistas, se contraiga dos veces (o más). Notemos que el centro de gravedad de la cruz (el punto $o$) se encuentra así mismo en en el centro del brazo. Consecuentemente, el movimiento vertical de la cruz (la caida o el giro del extremo delantero) es posible sólo si: (1) el centro $o$ y toda la línea central del brazo ($O'O''$) se encuentran sobre un espacio vacio, y (2) ninguno de los puntos $C, D, E, F$ tienen apoyo. Desde el punto de vista de un observador sobre la cruz, ésta se deslizará sobre el nicho que se ha reducido dos veces, ya que sobre la placa se apoyará siempre o el brazo y uno de los extremos o ambos extremos. El famoso truco mediante el giro de la varilla no puede darse aquí (analizaremos tal problema más adelante). No obstante, desde el punto de vista del observador sobre la placa, la cruz (que se ha reducido dos veces) cae al nicho. Así pues, tenemos dos sucesos diferentes: ¿ocurrió así la caida (un empujón sobre el plano) o no? ¿Y que pasará con el observador que esté en el nicho (lo aplastará o no)? ¿O para salvarse necesita urgentemente acelerarse hasta la velocidad de la cruz? ¿O es necesario que esté cerca del extremo $A'H'$ (o $D'E'$), a donde no llegará la cruz reducida?