La relatividad de la simultaneidad

Después de la crítica al concepto básico del tiempo, continuemos el análisis de las bases lógicas de esta teoría y analicemos el concepto auxiliar de la "relatividad de la simultaneidad". Recordemos el experimento mental de la TER. Sea que por una vía se mueve un tren $A'B'$ a una velocidad $v$. En la imágen de la vía ($C$) frente al centro del tren $C'$ (en el momento en que los puntos coinciden $C=C'$) cae un rayo. Entonces, en el sistema anclado al tren en movimiento el resplandor alcanza al mismo tiempo los puntos $A'$ y $B'$, mientras que para un observador en reposo el resplandor alcanza al mismo tiempo los puntos $A$ y $B$ (cuyo centro está en $C$). Pero en ese momento los puntos $C$ y $C'$ (los centros de los segmentos) se habrán separado una cierta distancia. No obstante, también en la física clásica es posible una situación semejante si queremos transmitir la información de los puntos $A', B', A, B$ a un nuevo punto único $D$ (o al contrario, del punto $D$ a los puntos $A', B', A, B$) con una cierta velocidad finita $v_1$ (aquí la TER y el carácter constante de la velocidad de la luz no juegan ningún papel).

Se puede sugerir el siguiente modelo mecánico (Fig. 1.11).

Figura 1.11: El modelo mecánico de la relatividad de la simultaneidad.

Supongamos que 4 puntos materiales (sin la fuerza de gravedad) caen por pares a una velocidad $v_1$ sobre el punto $C$ (junto al paisaje de las vias del tren) y sobre el centro del tren $C'$, que llegará al punto $C''$ cerca del punto $C$ en el momento de la caída. Supongamos que en el punto $C$ y en el centro del tren se han colocado reflectores (espejos) ideales (triángulos isóceles de ángulo y de base $\alpha=\pi/4$). Entonces, dos partículas reflejadas en el cuadro de las vías (en el punto $C$) pasarán volando por ambos lados a una velocidad $v_1$ y alcanzarán al mismo tiempo los puntos $A$ y $B$ (en el clásico $\vert AB\vert=\vert A'B'\vert$). Para esto se requiere un tiempo $t=L/v_1$, donde $2L$ es la longitud del tren. Las otras dos partículas, habiéndose reflejado en el centro del tren $C'$, se moverán relativamente a las vías a una velocidad $v'=v_1+(v/\tan\alpha)=v_1+v$ hacia adelante y $v''=v_1-v$ hacia atrás. En el transcurso de este mismo tiempo $t$ la primera de estas particulas recorrerá el camino (hacia adelante) $L'=v_1t+vt$, y puesto que el tren recorrerá el camino $vt$, entonces la partícula alcanzará el punto $A'$. Análogamente para la segunda partícula $L'' = v_1t-vt$; por consiguente, ella alcanzará el punto $B'$. De esta manera, el suceso - la caida de los puntos sobre los reflectores - será registrado al mismo tiempo en los cuatro puntos: tanto en los puntos $A$ y $B$ (sobre las vías) como en los puntos los puntos $A'$ y $B'$ (sobre el tren). Esto era el caso, cuando las partículas, que caían sobre el tren, participaban en su movimiento de inercia. Si el segundo par de las partículas (en el cuadro de las vías) cae sobre el punto inmóvil $C''$ en seguida, el reflector triangular en el tren (solamente a él) debe tener las esquinas siguientes a la base: contra el movimiento del tren - $alpha_3=0,5arctg(v1/v)$, y en la dirección del movimiento del tren - $alpha_4=Pi/2-x$. En este caso las partículas volarán en paralelo al tren y alcanzarán sus finales simultáneamente (¡pero no simultáneamente con el segundo par de las partículas!) . 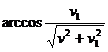Si queremos, que todos cuatro puntos materiales "hayan volado por" los puntos correspondientes $A', B', A, B$ simultáneamente, las esquinas a la base del reflector (en el tren) deben ser reducidas todavía a la esquina $ArcCos(v1/Sqrt(v^2+v1^2))$ (si establecer una plano guía de ondas, el par de las partículas sobre el tren no se "levantará" demasiado alto, y se moverá en paralelo al tren). Al parecer, los analogías mecánicos son posibles para las situaciones más diferentes.

Se puede decir que éstos son dos sucesos diferentes. Así pues, como en el caso del destello de luz (rayo), también son dos. Efectivamente, supongamos que el destello de luz tiene lugar en el momento en que coinciden los dos centros $O$ y $O'$ de los sistemas $S$ y $S'$, que se mueven uno respecto del otro a una velocidad ${\bf v}$. En un determinado momento $t>0$ el frente de la luz se encuentra sobre la esfera $\Sigma$ con relación al centro $O$ en el sistema $S$ y en la esfera $\Sigma'$ con centro en el sistema $S'$ (lo cual parece imposible). Sin embargo, aquí no hay nada del otro mundo (contradicciones con la física clásica), ya que el observador en el sistema $S$ registra la luz con una cierta frecuencia $\omega$, mientras que el observador en el sistema $S'$ registra esa misma luz pero en otra frecuencia $\omega'$ (a consecuencia del efecto Doppler). Y estos son ya dos sucesos diferentes que se pueden identificar: ¡al encontrarse, los observadores siempre pueden comparar los resultados de las mediciones $\omega$ y $\omega'$!

Analicemos ahora detalladamente el siguente experimento mental que demuestra la relatividad de la simultaneidad. Supongamos que el destello de luz ocurre en el momento en que coinciden los centros $O$ y $O'$ de los sistemas $S$ y $S'$, que se mueven uno respecto al otro, en el punto $O=O'$. De acuerdo a la TER, en el tiempo $\Delta t=t_1-t_{01}$, según el reloj del sistema $S$ la luz recorrerá una distancia $c(t_1-t_{01})$ a partir del centro $O$. En ese mismo tiempo $\Delta t=t_2-t_{02}$, según el reloj del sistema $S'$ esa misma luz recorrerá la distancia $c(t_2-t_{02})$ a partir del centro $O'$. La concordancia de los tiempos iniciales no influye en la diferencia de los tiempos $\Delta t$ y puede ser realizada igualmente antes o después del experimento con ayuda de cualquier método. Por ejemplo, se puede utilizar una fuente periódica infinitamente alejada, colocada perpendicularmente respecto a la dirección del movimiento. Se puede uno poner de acuerdo con antelación acerca de los destellos según el reloj del sistema $S$ (por ejemplo, periódicamente cada millón de años) y el sistema $S'$ se puede " organizar" un instante antes del destello elegido con antelación (en la Sección 1.7 se analizará la paradoja de la no-localidad relacionada con esto).

Recordemos que la principal idea positiva de la TER consistió en el carácter finito de la velocidad de transmisión de las interacciones. Esta misma idea es expresada por la teoría de la acción a corta distancia y refleja el planteamiento desde el punto de vista del campo (a través de las ecuaciones de Maxwell): el frente de luz desde la fuente hasta el receptor pasa sucesivamente por todos los puntos intermedios del espacio. Precisamente con esta propiedad entra en contradicción el concepto de la relatividad de la simultaneidad (Fig. 1.12).

Figura 1.12: Las contradicciones de la relatividad de la simultaneidad.

Para demostrar esto utilizaremos dos aseveraciones de la TER: 1. un mismo destello de luz alcanza al mismo tiempo a observadores que se mueven uno respecto al otro, sin importar que durante el tiempo de recorrido de la luz los observadores se habrán alejado una cierta distancia uno del otro. 2. las fórmulas cinemáticas de la TER (de los libro de texto) contienen solo el cuadrado de la luz. Supongamos, por ejemplo, que el primer observador en el sistema $S'$ se mueve en dirección hacia la fuente del destello a una velocidad pequeña $v\sim 10^4$ m/s. Puesto que la distancia hacia el punto del destello es muy grande (millones de años luz), entonces en el transcurso de un millón de años ambos observadores se separarán una gran distancia $\sim 2\cdot 10^{17}$ m. Según las fórmulas de la TER el tiempo de llegada de la señal para cada uno de los observadores será idéntico. ¿En qué punto del espacio el primer observador "dejó pasar" el frente de luz para el segundo observador? ¿Y si él sostuvo el espejo todo el millón de años pero lo bajó un segundo antes de que se registrase la señal? Según la opinión del segundo observador la señal fue reflejada por el primero en algún lugar adelante. ¿Y qué reflejó el primer observador si sus aparatos aun no han reaccionado ante el destello? Análogamente, un tercer observador puede alejarse del segundo a esa misma velocidad pero en la dirección que viene desde la fuente. ¿Verá o no el tercer observador la luz si el segundo sostiene el espejo un millón de años menos un segundo?

Por un lado, ya que en las fórmulas de la TER entra sólo el cuadrado de la velocidad, entonces el segundo observador considerará iguales los tiempos de recepción de la señal del primer y el tercer observadores. Los observadores pueden ponerse de acuerdo para enviar cada quien adicionalmente y sin demora sus propias señales en el momento de la recepción de las señales investigadas. Entonces, si los cálculos del segundo observador son ciertos, él debe obtener al mismo tiempo las señales del primer y tercer observadores (el problema es simétrico). Pero, por otro lado, de acuerdo a las ecuaciones de Maxwell la luz se transmite ininterrumpidamente y el segundo observador recibirá la señal del primero al mismo tiempo que él mismo verá la señal investigada. Según la opinión del segundo observador la luz en ese momento aun no habrá llegado al tercer observador. De esta manera, el segundo observador llegará a una contradicción con él mismo: los primeros cálculos mediante las fórmulas de la TER contradicen los segundos cálculos hechos mediante las ecuaciones de Maxwell. Es obvio que los observadores no verán el destello de forma simultánea, sino sucesivamente, ya que el camino espacial de la luz es único: la fuente, el primer observador, después el segundo y, finalmente, el tercer observador.

Notemos, adicionalmente, que incluso en el marco de la TER el concepto de la relatividad de la simultaneidad está fuertemente limitado: es aplicable sólo a dos sucesos aislados (no hay ni causas originales que se intersecten, ni consecuencias que se intersecten ni, hablando en general, nos interesa ningún otro hecho adicional). En realidad, incluso estos puntos elegidos tienen conos de luz que se intersectan y no hablemos ya de todos los otros puntos en el espacio y en el tiempo. Realmente tenemos cadenas completas de sucesos causalmente enlazados (y no enlazados) que mediante todo un conjunto de intersecciones pasan por cada uno de los puntos del espacio y del tiempo (raramente cada causa provoca la consecuencia correspondiente a la velocidad de la luz). Y toda esta red temporal real (¡de diversas dimensiones!) está interrelacionada en todo el espacio. Consecuentemente, en el caso general no podemos cambiar (mediante la elección del sistema de coordenadas) el orden de seguimiento incluso para los sucesos no enlazados causalmente (de cualquier modo esto se vería reflejado en algún lugar).