La théorie des collisions et les lois de la conservation dans la TRR

Très souvent dans la TRR on utilise le passage à un système de référence qui "se déplace d'une manière convenable" pour la "simplification" de la description des collisions. Pourtant ce procédé n'a aucun fondement physique et cela n'est pas lié avec le principe de la relativité pour les systèmes closes identiques. Si on fait les expériences relativistes sur des faisceaux des particules artificiels, les sources (les accélérations) et des appareils d'enregistrement sont attachés à la Terre et notre imagination ne les fera pas voler avec un observateur en mouvement. Si un certain processus est étudié dans la chambre de Wilson, les pistes des particules sont attachées au milieu (c'est-à-dire à la chambre de Wilson), pas à l'observateur volant. Par exemple dans la physique classique l'angle entre les pistes des particules ne dépend pas des mouvement de l'observateur. En même temps l'angle entre les vitesses des particules, laissant les pistes mentionnées peut dépendre de la vitesse du mouvement de l'observateur. Dans la physique relativiste les angles entre les trajectoires et les vitesses des particules aussi dépendent de la vitesse de l'observateur selon les lois différentes. C'est pourquoi le passage au nouveau système de référence, quoi qu'il semble si vraisemblable du point de vue de la TRR, peut fortement déformer l'interprétation de la résolution, c'est-à-dire, n'importe quel processus ne doit être considéré que dans le système de l'observateur réel (de l'appareil enregistreur).

La considération du processus de la collision des deux particules (ponctuelles par principe dans la TRR) comme un mouvement plat est aussi une des déformations de la réalité. En effet, même lors de l'étude des caractéristiques statistiques des particules ponctuelles un appareil de mesure ne peut pas (pour le rapprochement au problème idéal du mouvement des deux points) se mouvoir et tourner avec chaque paire de particules d'une manière individuelle (et différente!), car sa position est fixée. En outre, les particules ponctuelles doivent être considérées comme un cas limite des particules réelles des dimensions finales, sinon on ne pourrait observer ni des collisions directes, ni des collisions des atomes et des molécules, les protons n'auraient pas de structures etc. Et dans ce cas les collisions des particules sont par principe en trois dimensions (la possibilité du mouvement plat est égale à zéro). Supposons, par exemple, que deux bulles pareilles (1 et 2) se rapprochent l'une de l'autre sur des lignes droites croisées dans l'espace (la distance minimale entre elles est mineure par rapport au diamètre de la bulle) avant une collision. Depuis le début de l'expérience nous ne pouvons pas tracer un plan à travers les droites en question. Néanmoins, prenons le milieu de la distance minimale entre les droites croisées (les trajectoires avant la collision) et traçons des droites d'intersection parallèles aux trajectoires en question. Maintenant supposons que l'unique plan $\alpha$ traverse les droites croisées (Figure 4.8).

**Figure 4.8:** Le mouvement non plan de deux particules.
$\begin{figure}\begin{center}\epsfxsize =10.0truecm \epsfbox{fig4dyn2.eps}\end{center}\end{figure}$

Et les centres des bulles se déplacent parallèlement à ce plan avant une collision: le centre de la première bulle est un peu au-dessus du plan et le centre de la seconde bulle est au-dessous du plan. Après la collision les bulles voleront sur des autres droites croisées. Et de nouveau il est impossible de tracer un plan à travers ces deux lignes droites. Répétons la procédure du transfert parallèle des lignes droites, sur lesquelles passent les trajectoires du mouvement après la collision, jusqu'au intersection au milieu. Traçons un plan $\beta$ à travers les lignes droites croisées (les centres des bulles de nouveau se mouvrons des cotés différents de ce plan). Pourtant "le plan avant la collision" ne coïncide pas avec "le plan après la collision", mais le traverse sous un certain angle.

Le second procédé: traçons un plan $\gamma$ à travers la trajectoire du mouvement de la première particule (les lignes droites croisées de son mouvement avant et après la collision), et le second plan $\delta$ à travers la trajectoire analogique du mouvement de la seconde particule. Pourtant, ces deux plans se croisent aussi sous un certain angle (Figure 4.9).

**Figure 4.9:** Le caractère tridimensionnel de la collision de deux particules.
$\begin{figure}\begin{center}\epsfxsize =10.0truecm \epsfbox{fig5dyn2.eps}\end{center}\end{figure}$

Que provient du caractère tridimensionnel du mouvement? Premièrement, pas tous les lien sont linéaires. Par exemple, même lors du mouvement linéaire uniforme des corps sur des lignes croisées, la distance entre les corps se présente comme fonction non linéaire du temps. Deuxièmement, notons les lois classiques de la conservation de l'impulsion (en projections) et de l'énergie:

$\displaystyle v_{1x} + v_{2x}$	$\textstyle =$	$\displaystyle v'_{1x} + v'_{2x}$	(4.3)
$\displaystyle v_{1y} + v_{2y}$	$\textstyle =$	$\displaystyle v'_{1y} + v'_{2y}$	(4.4)
$\displaystyle v_{1z} + v_{2z}$	$\textstyle =$	$\displaystyle v'_{1z} + v'_{2z}$	(4.5)
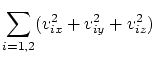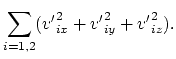$\displaystyle \sum_{i=1,2}(v^2_{ix} + v^2_{iy} + v^2_{iz})$	$\textstyle =$	$\displaystyle \sum_{i=1,2}({v'}^2_{ix} + {v'}^2_{iy} + {v'}^2_{iz}).$	(4.6)

Du système (4.3-4.6) nous voyons qu'il n'existe que quatre équations pour six grandeurs inconnues ( $v'_{1x}, v'_{1y}, v'_{1z}, v'_{2x}, v'_{2y}, v'_{2z}$ ). Donc, cela suppose que dans la résolution il y a deux paramètres indéterminés. Si on considère le mouvement comme plan (enlever l'équation (4.5)), on aura trois équations pour les quatre grandeurs inconnues qui restent. En conséquence lors de la comparaison des résolutions de la TRR avec celles de la physique classique on fait la substitution des résolutions et il en reste un seul paramètre indéterminé (d'habitude c'est l'angle de la dispersion). Cette fraude amène à l'interprétation fausse des données de l'expérience surtout lors de la restitution des grandeurs qui manquent. Par exemple, dans le livre [33] on analyse deux pistes de la détente des particules de la même masse et de la même charge (précisément du même rapport

?) à l'angle de la détente mineur à $90^{\circ}$ d'où on tire conclusion de l'inexqctitude de la mécanique classique. Notons la formule pour l'angle $\alpha$ entre les trajectoires des particules dispersantes:

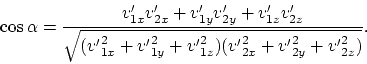$\begin{displaymath} \cos\alpha = {v'_{1x}v'_{2x} + v'_{1y}v'_{2y} + v'_{1z}v'_{2... ...1y} + {v'}^2_{1z})({v'}^2_{2x} + {v'}^2_{2y} + {v'}^2_{2z})}}. \end{displaymath}$

(4.7)

Choisissons l'axe

d'une manière que $v_{1z}=v_{2z}=0$ . Traduisons maintenant une variable ${v'}_{1x}$ de l'équation (4.3), traduisons la variable ${v'}_{1y}$ de l'équation (4.4) et traduisons la variable ${v'}_{1z}$ de l'équation (4.6) et traduisons la variable ${v'}^2_{2z}$ de l'équation (4.6) (et la condition ${v'}^2_{2z}>0$ limite le domaine des valeurs possibles de toutes les variantes). Mettons toutes les grandeurs nommées ci-dessus dans l'équation (4.7). Nous aurons comme résultat la dépendance deux-paramètrique des ${v'}_{2x}$ et ${v'}_{2y}$ , que nous omettons à cause de son grand volume. En utilisant un logiciel graphique on s'assure qu'avec les grandeurs en question $v_{1x}, v_{1y}, v_{2x}, v_{2y}$ nous recevons une certaine surface, ressemblant à la partie intérieure d'un cylindre, c'est-à-dire la grandeur $\cos~\alpha$ change dans de grandes limites. Par exemple, on peut facilement vérifier que les valeurs

$\begin{displaymath} v_{1x}=0,1; ~ ~ ~ v_{1y}=0,1; ~ ~ ~ v_{2x}=0,7; ~ ~ ~ v_{2y}=0,7; ~ ~ ~ v'_{1x}=0,6; \end{displaymath}$

$\begin{displaymath} v'_{2x}=0,2; ~ ~ ~ v'_{1y}=0,4; ~ ~ ~ v'_{2y}=0,4; ~ ~ ~ -v'_{2z}=v'_{1z}=\sqrt{0,14} \end{displaymath}$

répondent à toutes les lois classiques de la conservation (4.3-4.6). Pour ces valeurs recevons $\cos\alpha = 0,29554$ , c'est-à-dire $\alpha\approx 72,8^{\circ}$ . Remarquons: si les vitesses sont exprimées en unités de la vitesse de la lumière la vitesse minimale est tout à fait réelle pour le mouvement des électrons internes dans les atomes, en commencent par $z\ge 60$ . Et dans le cas général personne n'a vu des électrons au repos dans les atomes! Dans la physique classique l'angle égal à 90 $^{\circ}$ est reçu sans doute lors de la collision avec une particule au repos dans le système de l'appareil enregistreur (mais où trouver une particule pareille?). Pourtant, l'affirmation contraire du fait qu'une des particules était au repos (la probabilité mathématique de cette situation est très petite) ne provient pas de l'angle de la dispersion observé égal à 90 $^{\circ}$ . Donc, le problème inverse de la restitution des données, qui manquent est une procédure ambiguë et dans la physique classique et dans la physique relativiste (il existe une grandeur interminable de résolutions cohérentes et différentes).

Pour la vérification expérimentale plus stricte des lois de la conservation lors des collisions (sans dépendance de la théorie) il faut étudier les collisions des particules dans le vide pour les faisceaux étroits mono-énergétiques des particules connues avec les angles des collisions donnés. L'étude complète du processus de la collision doit inclure la vérification de la balance par moyen des énergies des particules (pour chaque angle de dispersion dans l'espace), la vérification de la balance des impulsions des particules, la vérification de la balance de la grandeur commune des particules dans des faisceaux avant et après la collision (la probabilité de la dispersion), la vérification de la balance des émissions surgissant par les énergies et les directions. Il existe encore deux questions auxquelles on prête l'attention (encore deux questions vagues): dépend la dispersion de l'orientation mutuelle des moments propres de la rotation des particules en collision? Les moments propres de la rotation lors des collisions, changent-ils? La physique classique donne la réponse affirmative à ces deux questions (mais du point de vue quantitatif elle dépend beaucoup de la "structure" des bulles).

L'auteur n'a jamais rencontré l'analyse complète d'un processus de la collision dans la TRR qui corresponde à tous les principes mentionnés. Cela n'amène pas à la conclusion de l'inexactitude (dans les cadres les erreurs expérimentales) des lois relativistes courantes de la conservation dans n'importe quel processus de la collision (bien que pour un grand nombre de cas cela puisse être vrai). L'auteur n'affirme qu'il n'existe même pas d'exemples isolés de l'affirmation absolue des lois relativistes de la collision (sans parler de la confirmation globale, qui est très publicitaire).

Ayant une attitude principalement stricte, l'application des lois relativistes de la conservation au processus de la collision dans la physique subnucléaire semble douteuse. Pourront-elles être gardées sans dépendance de la charge des particules en collision, des angles de la collision et des angles de la dispersion? C'est que lors du processus de la collision les particules chargées reçoivent une accélération. En conséquence, selon les idées contemporaines (y compris celles de la TRR) une certaine émission (champ) doit être toujours observée. Faudrait-il agir comme les étudiants, épiant la réponse d'un problème: si un appareil a enregistré un quantum gamma ("a pris la main dans le sac"), il faut l'absolument le prendre en compte "à l'air sage". Et dans les autres cas croire "à l'air sage" en justesse des formules de la TRR? En quoi consiste "la force prédictive" de la TRR? En réalité les lois de la conservation doivent être absolument complétées par les membres, prenant en compte l'énergie et l'impulsion du champ.

En général, le seul cas, quand la discussion des lois relativistes de la conservation lors des "collision" est valable, est l'interaction des particules par les forces d'origine électromagnétiques (la force de Lorentz). Dans les autres cas la réalisation des lois relativistes de la conservation est une hypothèse non vérifiée (des sphères lumineux de la TRR n'ont aucun rapport avec les forces d'origine non électromagnétique). Pourtant les interactions électromagnétiques n'exigent aucune des idées de la TRR pour la déduction des lois relatives de la conservation. On sait que les équations du mouvement aux conditions initiales déterminent complètement toutes les caractéristiques du mouvement, y compris des intégrales du mouvement. L'énergie peut servir de cette intégrale du mouvement (pas toujours). De l'équation du mouvement provient

$\begin{displaymath} {d{\bf P}\over dt} = {\bf F} ~ ~ \Rightarrow ~ ~ {\bf v}d{\bf P} = {\bf F}d{\bf r}. \end{displaymath}$

(4.8)

En connaissant la expression de l'impulsion (c'est une grandeur qui entre dans l'équation expérimentale du mouvement (4.8)), par exemple dans le cas classique

conformément. A condition de l'égalité des forces de l'action et de la réaction (la troisième loi de Newton, l'hypothèse des forces centrales) on reçoit: ${\bf F}_{12}=-{\bf F}_{21}$ . Alors de l'équation du mouvement (4.8) on peut déduire la loi de la conservation de l'impulsion (c'est une grandeur qui entre dans l'équation expérimentale du mouvement (4.8)): de $d{\bf P_1}/dt={\bf F}_{12},~ ~ d{\bf P_2}/dt={\bf F}_{21}$ recevons

$\begin{displaymath} {d({\bf P}_1+{\bf P}_2)\over dt} = 0, ~ ~ \Rightarrow ~ ~ {\bf P}_1+{\bf P}_2=const. \end{displaymath}$

Cependant avec les forces magnétiques ${\bf F}_{12}\ne -{\bf F}_{21}$ même la loi relativiste de la conservation de l'impulsion des particules dans le cas commun peut être troublée. Etant donné que la majorité de particules, et même la plupart des particules neutres, ont le moment magnétique (c'est-à-dire elles ne représentent pas "des charges ponctuelles idéales de la TRR", mais des rotateurs magnétiques chargés de dimensions finales), l'application de la loi relativiste de la conservation de l'impulsion dans la physique nucléaire et subnucléaire sans le compte évident de l'impulsion du champ n'est pas valable. Par conséquent nous arrivons de nouveau à la nécessité de l'enregistrement visible de l'impulsion du champ et, comme suite, de son énergie lors des collisions. (Peut-être, cela pourra régler la physique nucléaire et subnucléaire et réduire le nombre de particules-fantômes?)

Le compte de la force de la réaction de l'émission provoque l'infraction des lois de la conservation de l'énergie et de l'impulsion, déposées dans la TRR. S’il faut renoncer à l’enregistrement de cette force au cours des collisions des particules? Mais c'est que cette force y doit être la plus important (il y a de grands champs suite au rapprochement des particules dures (haut-énergiques) et de grandes accélérations variables).