Après la critique de la notion fondamentale du temps continuons l’analyse de
bases logiques de cette téorie et examinons la notion auxiliaire "la relativité
de la simultanéité". Rappelons une expérience mentale de la théorie de la
relativité restreinte. Supposons que le train ![]() roule sur le chemin de fer à une
vitesse
roule sur le chemin de fer à une
vitesse ![]() .
Un éclair frappe dans la voie du chemin de fer (
.
Un éclair frappe dans la voie du chemin de fer (![]() ) en face du centre de train
) en face du centre de train ![]() (au moment
de la coïncidence des points
(au moment
de la coïncidence des points ![]() ). Alors dans le système lié avec le train en
mouvement, l’éclat atteindra simultanément les points
). Alors dans le système lié avec le train en
mouvement, l’éclat atteindra simultanément les points ![]() et
et ![]() , tandis que pour un observateur
immobile l’éclat atteindra simultanément les points
, tandis que pour un observateur
immobile l’éclat atteindra simultanément les points ![]() et
et ![]() (avec le point
(avec le point ![]() au milieu), mais pour ce
moment les points
au milieu), mais pour ce
moment les points ![]() et
et ![]() (les milieux de segments) ne coïncideront pas pour une certaine
distance. Pourtant même dans la physique classique la situation suivante est
possible, si nous transmettrons l’information de points
(les milieux de segments) ne coïncideront pas pour une certaine
distance. Pourtant même dans la physique classique la situation suivante est
possible, si nous transmettrons l’information de points ![]() ,
, ![]() ,
, ![]() et
et ![]() dans le nouveau point unique
dans le nouveau point unique ![]() (ou à l'envers
- du point
(ou à l'envers
- du point ![]() en points
en points ![]() ,
, ![]() ,
, ![]() ,
, ![]() ) à une certaine vitesse
) à une certaine vitesse ![]() (en ce cas la théorie de la
relativité restreinte et la constance de la vitesse de la lumière ne joueront
aucun rôle).
(en ce cas la théorie de la
relativité restreinte et la constance de la vitesse de la lumière ne joueront
aucun rôle).
On peut proposer une modèle mécanique suivante (Figure 1.11).
Supposons que 4 points matériels tombent (sans gravité) à la vitesse On peut dire, que se sont deux événements différents. Mais dans le cas de
flash de la lumière (de l’éclat) ils sont aussi deux. Réellement, supposons
qu’un flash de lumière a lieu en moment de la coïncidence de centres Analysons maintenent plus en détail l’expérience imaginée, qui "démontre" la
relativité de la simultanéité: supposons qu’un flash de lumière a lieu en moment
de la coïncidence de centres Souvenons-nous, qu’une idée positive principale de la théorie de la
relativité restreinte consistait en ce que la vitesse de la transmission des
interactions est fine. La même idée est exprimée dans la théorie de l’action à
proximité et refléte l’approche de champs (via l’équation de Maxvel): le front
de lumière passe successivement tous les points intermédiaires de l’espace, de
la source jusqu’au récepteur. C’est justement avec cette propriété que la notion
de la relativité de la simultanéité esten contradiction. (Figure 1.12).
Pour la démostration de cela nous utiliserons deux affirmations de la théorie
de la relativité restreinte: 1) le même flash de la lumière simultanément
atteint les observateurs qui se déplacent l‘un à l’égard de l’autre, malgré ce
que pendant le temps du passage de la lumière les observateurs s’en iront l’un
de l’autre pour une certaine distance dans l’espace; 2) les formules
cinématiques de la théorie de la relativité restreinte (tirées de manuels)
contiennent seulement la vitesse au carré. Supposons, par exemple, que le
premier observateur dans le système D’une côté comme seulement la vitesse au carré entre dans les formules de la
théorie de la relativité restreinte, alors le deuxième observateur estimera que
le temps de la réception du signal par le premier et le troisième observateurs
est le même. On peut convenir de l’envoi sans retard supplémentaire de ses
signaux au moment de la réception du signal étudié par chaque observateur. Alors
si les calculs du deuxième observateur sont justes il doit recevoir les signaux
du premier et du troisième observateur en même temps (le problème est
symétrique). Cependant de l’autre côté selon les équations de Maxvell la lumière
se répand ininterrompuement et le deuxième observateur recevera le signal du
premier simultanément avec le signal étudié qu’il verra lui-même. A l’avis du
deuxième observateur la lumière n’arriva pas ecore au troisième observateur pour
ce temps-là. Ainsi le deuxième observateur contredit à lui même: les premiers
calculs selon les formules de la théorie de la relativité sont contraires aux
deuxièmes calculs faits selon les équations de Maxvel. Il est evident que les
observateurs ne verrons pas le flash simultanéiment, mais successivement car le
chemin spatial de la lumière est unique: la source, le premier observateur, puis
le deuxième et, enfin, le troisième.
En plus il faut noter que même dans les cadres de la théorie de la relativité
restreinte la notion de la relativité de la simultanéité est fort limitée: elle
est appliquable seulement à deux événements isolés (s’il n’y a pas de causes
initiales qui se croisent, il n’y a pas de conséquences qui se croisent et en
général aucuns faits supplémentaires ne nous intéressent pas). En réalité même
pour ses points choisis les cônes de lumière ont les intersections, on en passe
tous les autres points dans l’espace et le temps. En fait nous avons les chaînes
ininterrompues des événements liés (et ceux qui ne sont pas liés) en causes et
en conséquences, qui passent avec beaucoup d’intersections dans chaque point de
l’espace et du temps (rien moins que chaque cause provoque une conséquence
correspondante à la vitesse de la lumière). Et ce filet temporel réel (à
l’échelle différente!) est en corrélation pour tout espace. C’est-à-dire, en cas
général on ne peut pas changer (en choisissant une autre système de référence)
l’ordre de la succétion même d’événement qui ne sont pas liées par les causes
(cela se refléterait sans doute quelque part).
![]() deux à deux
au-dessus du point
deux à deux
au-dessus du point ![]() (à côté du chemin de fer) et au-dessus du centre du
train
(à côté du chemin de fer) et au-dessus du centre du
train ![]() , qui arrivera au point
, qui arrivera au point ![]() (à côté du point
(à côté du point ![]() ) vers le moment de la chute. Supposons que dans le point
) vers le moment de la chute. Supposons que dans le point ![]() et au milieu
du train les réflecteurs idéals sont installés (les triangles isocèles avec
l’angle à la base
et au milieu
du train les réflecteurs idéals sont installés (les triangles isocèles avec
l’angle à la base ![]() ). Alors deux particules reflétées au-dessus du chemin de
fer (en point
). Alors deux particules reflétées au-dessus du chemin de
fer (en point ![]() ) bifurqueront à la vitesse
) bifurqueront à la vitesse ![]() et atteindront les points
et atteindront les points ![]() et
et ![]() (en classique
(en classique ![]() ). Cela demande le temps
). Cela demande le temps ![]() , où
, où ![]() est la longueur du train. Deux autres
particules, reflétées au-dessus du milieu du train
est la longueur du train. Deux autres
particules, reflétées au-dessus du milieu du train ![]() se déplaceront relativement au
chemin de fer à de vitesses
se déplaceront relativement au
chemin de fer à de vitesses ![]() en avant et
en avant et ![]() en arrière.
En ce même temps
en arrière.
En ce même temps ![]() la première particule fera le chemin (en avant)
la première particule fera le chemin (en avant) ![]() , et comme
le train fera le chemin
, et comme
le train fera le chemin ![]() , alors la particule atteindra le point
, alors la particule atteindra le point ![]() . Par analogie, pour
la deuxième particule
. Par analogie, pour
la deuxième particule ![]() ; par conséquent elle atteindra le point
; par conséquent elle atteindra le point ![]() . Ainsi,
l’événement - la chute des particules sur les réflecteurs - sera fixé dans tous
les quatres points: dans les points
. Ainsi,
l’événement - la chute des particules sur les réflecteurs - sera fixé dans tous
les quatres points: dans les points ![]() et
et ![]() (au-dessus du chemin de fer), comme dans les
points
(au-dessus du chemin de fer), comme dans les
points ![]() et
et ![]() (au-dessus du train).
C'était le cas, quand les particules, tombant au-dessus du train, participaient à son mouvement inertiel.
Si la deuxième paire des particules (sur du chemin de fer) tombe tout d'un coup sur le point immobile
(au-dessus du train).
C'était le cas, quand les particules, tombant au-dessus du train, participaient à son mouvement inertiel.
Si la deuxième paire des particules (sur du chemin de fer) tombe tout d'un coup sur le point immobile ![]() , le réflecteur triangulaire au train (seulement à cela) doit avoir les angles
suivants à la base: contre du mouvement du train -
, le réflecteur triangulaire au train (seulement à cela) doit avoir les angles
suivants à la base: contre du mouvement du train - ![]() , mais en direction le mouvement du train -
, mais en direction le mouvement du train - ![]() . Dans ce cas les particules voleront parallèlement vers le train et atteindront ses fins simultanément
(mais non simultanément avec la deuxième paire de particules!). Si nous voulons, que tous quatre particules
"aient volé" sur les points correspondants
. Dans ce cas les particules voleront parallèlement vers le train et atteindront ses fins simultanément
(mais non simultanément avec la deuxième paire de particules!). Si nous voulons, que tous quatre particules
"aient volé" sur les points correspondants ![]() ,
, ![]() ,
, ![]() ,
, ![]() simultanément,
les angles à la base du réflecteur (au train) doivent être diminués encore de l'angle
simultanément,
les angles à la base du réflecteur (au train) doivent être diminués encore de l'angle 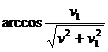 (si établir une vaguelette plate, la paire des particules
au-dessus du train "ne montera pas" trop haut, mais se déplaceront parallèlement au train).
Comme on voit, les analogies mécaniques sont possibles pour les plus différentes situations.
(si établir une vaguelette plate, la paire des particules
au-dessus du train "ne montera pas" trop haut, mais se déplaceront parallèlement au train).
Comme on voit, les analogies mécaniques sont possibles pour les plus différentes situations.
![]() et
et ![]() de
systèmes
de
systèmes ![]() et
et ![]() ,
qui se déplacent l’un relativement à l’autre à la vitesse
,
qui se déplacent l’un relativement à l’autre à la vitesse ![]() . En certain
moment de temps
. En certain
moment de temps ![]() le front du temps se trouvera sur une sphère
le front du temps se trouvera sur une sphère ![]() relativement au centre
relativement au centre ![]() dans le système
dans le système ![]() et sur une sphère
et sur une sphère ![]() relativement au centre
relativement au centre ![]() dans le
système
dans le
système ![]() (ce que semble impossible). Mais il n’y a rien d’étonnant (pas de
contradiction avec la physique classique), parce qu’un observateur dans le
système
(ce que semble impossible). Mais il n’y a rien d’étonnant (pas de
contradiction avec la physique classique), parce qu’un observateur dans le
système ![]() fixera la lumière d’une certaine fréquence uniforme
fixera la lumière d’une certaine fréquence uniforme ![]() , alors qu’un observateur dans
le système
, alors qu’un observateur dans
le système ![]() fixera la même lumière, mais de l’autre fréquence
fixera la même lumière, mais de l’autre fréquence ![]() (par suite de
l’effet de Doppler). Mais c’est déja deux événements identifiés comme
différents: au moment de la rencontre les observateurs pourront toujours
comparer les résultats de mesures de
(par suite de
l’effet de Doppler). Mais c’est déja deux événements identifiés comme
différents: au moment de la rencontre les observateurs pourront toujours
comparer les résultats de mesures de ![]() et de
et de ![]() !
!
![]() et
et ![]() des systèmes
des systèmes ![]() et
et ![]() , qui se déplacent l’un à l’égard de l’autre,
dans le point
, qui se déplacent l’un à l’égard de l’autre,
dans le point ![]() . D’après TRR la lumière passera la distance
. D’après TRR la lumière passera la distance ![]() du centre
du centre
![]() pendant le
temps
pendant le
temps ![]() selon l’horloge du système
selon l’horloge du système ![]() . La même lumière fera la
distance
. La même lumière fera la
distance ![]() du centre
du centre ![]() pendant le même temps
pendant le même temps ![]() selon l’horloge du système
selon l’horloge du système ![]() . La conciliation des temps initiaux n’influence pas sur
la différence de temps
. La conciliation des temps initiaux n’influence pas sur
la différence de temps ![]() et peut être vérifiée comme avant l’expérience même
qu’après par n’importe quelle méthode. Par example on peut utiliser une source
périodique infiniment éloignée, qui se trouve perpendiculairement à la direction
du mouvement. On peut convenir d’avance de flashs selon l’horloge du système
et peut être vérifiée comme avant l’expérience même
qu’après par n’importe quelle méthode. Par example on peut utiliser une source
périodique infiniment éloignée, qui se trouve perpendiculairement à la direction
du mouvement. On peut convenir d’avance de flashs selon l’horloge du système
![]() (par
exemple, chaque million d’années périodiquement), et "organiser" le système
(par
exemple, chaque million d’années périodiquement), et "organiser" le système ![]() un instant
avant d’un flash choisi d’avance (dans la division 1.7 on examinera le paradoxe
de l’illocalité lié avec cela).
un instant
avant d’un flash choisi d’avance (dans la division 1.7 on examinera le paradoxe
de l’illocalité lié avec cela).
![]() se déplace vers la source du flash à une petite
vitesse
se déplace vers la source du flash à une petite
vitesse ![]() m/s. Comme la distance jusqu’au source du flash est grande (un million
d’années lumières), dans un million d’années les deux observateurs s’en iront
pour une grande distance de
m/s. Comme la distance jusqu’au source du flash est grande (un million
d’années lumières), dans un million d’années les deux observateurs s’en iront
pour une grande distance de ![]() mètres. Selon les formules de
la théorie de la relativité restreinte le temps de l’arrivée du signal pour
chaque observateur sera le même. Dans lequel point de l’espace l’un des
observateurs "laissa passer" le front de lumière pour le deuxième observateur?
Et si tout le million d’année il tenait un miroir, mais une seconde avant la
réception du signal il l’enleverait? Dans l’avis d’un second observateur le
signal est reflété par le premier observateur quelque part en avant. Mais
qu’est-ce que le premier observateur reflétait si ses appareils ne réagissaient
pas encore au flash. Par analogie le troisième observateur peut s’eloigner du
deuxième à une même vitesse, mais dirigée du côté de la source. Le troisième
observateur, verra-t-il la lumière, si le deuxième tient le miroir un million
d’années moins une seconde?
mètres. Selon les formules de
la théorie de la relativité restreinte le temps de l’arrivée du signal pour
chaque observateur sera le même. Dans lequel point de l’espace l’un des
observateurs "laissa passer" le front de lumière pour le deuxième observateur?
Et si tout le million d’année il tenait un miroir, mais une seconde avant la
réception du signal il l’enleverait? Dans l’avis d’un second observateur le
signal est reflété par le premier observateur quelque part en avant. Mais
qu’est-ce que le premier observateur reflétait si ses appareils ne réagissaient
pas encore au flash. Par analogie le troisième observateur peut s’eloigner du
deuxième à une même vitesse, mais dirigée du côté de la source. Le troisième
observateur, verra-t-il la lumière, si le deuxième tient le miroir un million
d’années moins une seconde?
![]()
![]()
![]()
suivant: Les transformation de Lorentz
monter: La cinématique de la
TRR précédent: Les remarques
supplémentaires
Sergey N. Artekha