Nächste: Impulsmoment in der SRT Nach oben: Kritik der allgemeingültigen Interpretation Vorhergehende: Nochmals von der Masse Inhaltsverzeichnis
Sehr oft wendet man in der SRT für die „Vereinfachung“ der Beschreibung von Stößen das Verfahren des Übergangs in irgendwelches „bequem bewegte“ Bezugssystem an. Aber solches Vorgehen legt keine physischen Gründe vor, und das Relativitätsprinzip für geschlossene identische Systeme hat damit nichts zu tun. Wenn relativistische Experimente mit künstlichen Bündeln von Teilchen angestellt werden, sind die Quellen (Beschleuniger) und Registriergeräte an die Erde gebunden, und Beschleuniger und Geräte werden doch mit dem bewegten Beobachter infolge unserer Gedankenvorstellung nicht fliegen. Wird ein gewisser Prozess in der Wilson-Kammer erforscht, so sind die Teilchenspuren an das Medium (d.h., an die Wilson-Kammer) und nicht an den fliegenden Beobachter gebunden. In der klassischen Physik, z.B., wird der Winkel zwischen den Teilchenspuren von der Bewegung des Beobachters nicht verändert. Gleichzeitig kann der Winkel zwischen den Geschwindigkeiten von Teilchen, die die angegebenen Spuren verlassen, von der Geschwindigkeit des Beobachters abhängen. In der relativistischen Physik hängen die Winkel zwischen den Bahnen und zwischen den Geschwindigkeiten von Teilchen laut verschiedenen Gesetzen von der Geschwindigkeit der Bewegung des Beobachters ab. Darum kann der Übergang, der vom SRT-Standpunkt aus angeblich glaubenswürdig ist, zum neuen Bezugssystem die Interpretation der Lösung wesentlich verdrehen, d.h., jeder Prozess soll nur im System des realen Beobachters (Registriergerätes) betrachtet werden.
Noch eine Verstellung der Wirklichkeit ist die Betrachtung des Stoßprozesses von zwei Teilchen (in der SRT grundsätzlich Punktteilchen) als ebener Bewegung. In der Tat kann (für Anpassung an ideale Aufgabe der Bewegung von zwei Punkten) das Messgerät sogar bei der Forschung der statistischen Charakteristiken von Punktteilchen mit jedem Teilchenpaar nicht fliegen und sich auf eigene Art und Weise nicht drehen (verschieden!), die Lage des Gerätes ist fixiert. Außerdem sollen die Punktteilchen als Grenzfall von Teilchen mit realer endlicher Größe betrachtet werden, sonst könnte man zentrale Stöße nicht beobachten, man könnte sich die Stöße von Atomen und Molekülen nicht anschauen, Protonen hätten keine Struktur usw. In diesem Fall ist der Stoß von Teilchen grundsätzlich dreidimensional (die Wahrscheinlichkeit der ebenen Bewegung ist gleich Null). Mögen, z.B., sich zwei gleiche Kügelchen (1 und 2)einander vor dem Stoß auf den sich im Raum kreuzenden Geraden nähern (die minimale Entfernung zwischen den Geraden kleiner als Durchmesser vom Kügelchen). Schon vom Anfang des Experiments an können wir durch diese vorgegebenen Geraden keine Ebene ziehen. Trotzdem nehmen wir die Mitte der minimalen Entfernung zwischen den sich kreuzenden Geraden (Bahnen vor dem Stoß) und ziehen die sich kreuzenden parallelen den gegebenen Bahnen Geraden durch sie.
Jetzt geht die einzige Ebene ![]() (Abb. 4.8) durch die
sich kreuzenden Geraden durch. Die Mittelpunkte von Kügelchen bewegen sich vor
dem Stoß parallel dieser Ebene: der Mittelpunkt vom ersten Kügelchen bewegt sich
ein bisschen höher von der Ebene, der Mittelpunkt vom zweiten Kügelchen ein
bisschen tiefer von dieser Ebene. Nach dem Stoß fliegen die Kügelchen auf
anderen sich kreuzenden Geraden. Man kann wieder durch diese Geraden keine Ebene
ziehen. Wieder machen wir eine analoge Prozedur mit dem parallelen Übertragen
von Geraden, auf deren die Bewegungslinien nach dem Stoß liegen, bis zur
Kreuzung in der Mitte. Ziehen wir die Ebene
(Abb. 4.8) durch die
sich kreuzenden Geraden durch. Die Mittelpunkte von Kügelchen bewegen sich vor
dem Stoß parallel dieser Ebene: der Mittelpunkt vom ersten Kügelchen bewegt sich
ein bisschen höher von der Ebene, der Mittelpunkt vom zweiten Kügelchen ein
bisschen tiefer von dieser Ebene. Nach dem Stoß fliegen die Kügelchen auf
anderen sich kreuzenden Geraden. Man kann wieder durch diese Geraden keine Ebene
ziehen. Wieder machen wir eine analoge Prozedur mit dem parallelen Übertragen
von Geraden, auf deren die Bewegungslinien nach dem Stoß liegen, bis zur
Kreuzung in der Mitte. Ziehen wir die Ebene ![]() durch
sich kreuzende Geraden (wieder werden sich die Mittelpunkte von Kügelchen auf
verschiedenen Seiten dieser Ebene bewegen). Aber „die Ebene vor dem Stoß“ fällt
mit der „Ebene nach dem Stoß“ nicht zusammen, sondern überquert sie unter
gewissem Winkel.
durch
sich kreuzende Geraden (wieder werden sich die Mittelpunkte von Kügelchen auf
verschiedenen Seiten dieser Ebene bewegen). Aber „die Ebene vor dem Stoß“ fällt
mit der „Ebene nach dem Stoß“ nicht zusammen, sondern überquert sie unter
gewissem Winkel.
Das zweite Verfahren: ziehen wir die eine Ebene ![]() durch die Spur der Bewegung vom ersten Teilchen (die sich
kreuzenden Geraden seiner Bewegung vor und nach dem Stoß) und die zweite Ebene
durch die Spur der Bewegung vom ersten Teilchen (die sich
kreuzenden Geraden seiner Bewegung vor und nach dem Stoß) und die zweite Ebene
![]() durch analoge Spur der Bewegung vom zweiten
Teilchen. Aber diese Ebenen kreuzen sich auch unter gewissem Winkel
(Abb. 4.9).
durch analoge Spur der Bewegung vom zweiten
Teilchen. Aber diese Ebenen kreuzen sich auch unter gewissem Winkel
(Abb. 4.9).
Was folgt aus der Dreigemessenheit der Bewegung? Erstens. Nicht alle
Verbindungen erweisen sich linear. Z.B., sogar bei geradliniger gleichmäßiger
Bewegung von Körpern auf den sich kreuzenden Geraden stellt sich die Entfernung
zwischen Körpern als nichtlineare Zeitfunktion heraus. Zweitens. Schreiben wir
die klassischen Erhaltungssätze von Impuls (in Abbildungen) und Energie auf:
| (4.3) | |||
| (4.4) | |||
| (4.5) | |||
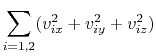 |
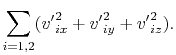 |
(4.6) |
Vom System (4.3-4.6) sehen wir, dass es nur vier Gleichungen für sechs
unbekannte Größen ( ![]() ) gibt. Solcherweise sollen zwei unbestimmte Parameter in der Lösung bleiben. Hält man die
Bewegung für die ebene (die Gleichung (4.5) wegtun), werden wir drei Gleichungen
für die vier gebliebenen Unbekannten haben. Es wird also die Unterschiebung der
Lösungen beim Vergleich der SRT-Lösungen mit der klassischen Physik
verwirklicht, und es bleibt nur ein unbestimmter
Parameter (gewöhnlich hält man für solchen den Streuwinkel). Solche
Unterschiebung führt zur unrichtigen Interpretation der Daten vom Experiment,
besonders bei Wiederherstellung von fehlenden Größen. Im Buch [33], z.B., werden
zwei Spuren der Zerstreuung von Teilchen gleicher Masse und Ladung (genauer
gesagt, der Relation
) gibt. Solcherweise sollen zwei unbestimmte Parameter in der Lösung bleiben. Hält man die
Bewegung für die ebene (die Gleichung (4.5) wegtun), werden wir drei Gleichungen
für die vier gebliebenen Unbekannten haben. Es wird also die Unterschiebung der
Lösungen beim Vergleich der SRT-Lösungen mit der klassischen Physik
verwirklicht, und es bleibt nur ein unbestimmter
Parameter (gewöhnlich hält man für solchen den Streuwinkel). Solche
Unterschiebung führt zur unrichtigen Interpretation der Daten vom Experiment,
besonders bei Wiederherstellung von fehlenden Größen. Im Buch [33], z.B., werden
zwei Spuren der Zerstreuung von Teilchen gleicher Masse und Ladung (genauer
gesagt, der Relation ![]() ?) mit dem Streuwinkel
kleiner
?) mit dem Streuwinkel
kleiner ![]() demonstriert, und daraus zieht man die Schlussfolgerung von Unrichtigkeit der
klassischen Physik. Schreiben wir den Ausdruck für den Winkel
demonstriert, und daraus zieht man die Schlussfolgerung von Unrichtigkeit der
klassischen Physik. Schreiben wir den Ausdruck für den Winkel ![]() zwischen den Spuren von zerstreuenden Teilchen auf:
zwischen den Spuren von zerstreuenden Teilchen auf:
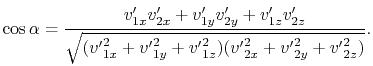 |
(4.7) |
Wählen wir die Achse ![]() so, dass
so, dass ![]() . Drücken wir jetzt die Variable
. Drücken wir jetzt die Variable ![]() von der
Gleichung (4.3) aus, die Variable
von der
Gleichung (4.3) aus, die Variable ![]() von der
Gleichung (4.4), die Variable
von der
Gleichung (4.4), die Variable ![]() von der Gleichung (4.5),
und von der Gleichung (4.6) die Größe
von der Gleichung (4.5),
und von der Gleichung (4.6) die Größe ![]() (die
Voraussetzung
(die
Voraussetzung ![]() beschränkt dabei den Bereich von Größen aller Variablen). Substituieren wir alle
oben genannten Größen in die Gleichung (4.7). Es ergibt sich die
zweiparametrische Abhängigkeit von
beschränkt dabei den Bereich von Größen aller Variablen). Substituieren wir alle
oben genannten Größen in die Gleichung (4.7). Es ergibt sich die
zweiparametrische Abhängigkeit von ![]() und
und
![]() , die wir wegen ihrer Sperrigkeit nicht
ausschreiben. Unter Anwendung graphischer Programme kann man sich davon
überzeugen, dass sich eine Fläche bei den vorgegebenen Größen
, die wir wegen ihrer Sperrigkeit nicht
ausschreiben. Unter Anwendung graphischer Programme kann man sich davon
überzeugen, dass sich eine Fläche bei den vorgegebenen Größen ![]() bildet, die dem Innenteil des Zylinders ähnlich aussieht, d.h.,
die Größe
bildet, die dem Innenteil des Zylinders ähnlich aussieht, d.h.,
die Größe ![]() in
weiten Grenzen verändert wird. Z.B., es ist leicht zu prüfen, dass die Größen
in
weiten Grenzen verändert wird. Z.B., es ist leicht zu prüfen, dass die Größen
alle klassischen Erhaltungssätze (4.3-4.6) zufriedenstellen. Für diese Größen
erhalten wir ![]() , d.h.,
, d.h., ![]() . Es sei bemerkt: rechnet man
Geschwindigkeiten in Einheiten der Lichtgeschwindigkeiten ausgedrückt, ist die
kleinere Geschwindigkeit für die Bewegung der Innenelektronen in Atomen ganz
real, von
. Es sei bemerkt: rechnet man
Geschwindigkeiten in Einheiten der Lichtgeschwindigkeiten ausgedrückt, ist die
kleinere Geschwindigkeit für die Bewegung der Innenelektronen in Atomen ganz
real, von ![]() beginnend. Im allgemeinen Fall hat keiner
ja auch ruhende Elektronen in Atomen gesehen! Der Winkel
beginnend. Im allgemeinen Fall hat keiner
ja auch ruhende Elektronen in Atomen gesehen! Der Winkel ![]() ergibt sich eindeutig in
der klassischen Physik beim Stoß mit dem ruhenden Teilchen im System des
Registriergerätes (wo ist nur solch ein Teilchen zu finden?). Aber aus dem
beobachtenden Streuwinkel von 90 folgert keine gegenteilige Bestätigung mit
Eindeutigkeit, dass eines von Teilchen ruhte (die mathematische
Wahrscheinlichkeit solchen Ereignisses ist unendlich klein). So ist die
entgegengesetzte Aufgabe der Wiederherstellung von fehlenden Daten kein
eindeutiges Verfahren weder in der klassischen, noch in der relativistischen
Physik (es gibt eine unendliche Zahl der nicht widersprechenden Lösungen).
ergibt sich eindeutig in
der klassischen Physik beim Stoß mit dem ruhenden Teilchen im System des
Registriergerätes (wo ist nur solch ein Teilchen zu finden?). Aber aus dem
beobachtenden Streuwinkel von 90 folgert keine gegenteilige Bestätigung mit
Eindeutigkeit, dass eines von Teilchen ruhte (die mathematische
Wahrscheinlichkeit solchen Ereignisses ist unendlich klein). So ist die
entgegengesetzte Aufgabe der Wiederherstellung von fehlenden Daten kein
eindeutiges Verfahren weder in der klassischen, noch in der relativistischen
Physik (es gibt eine unendliche Zahl der nicht widersprechenden Lösungen).
Für eine strengere experimentelle Prüfung der Erhaltungssätze bei Zusammenstößen (unabhängig von der Theorie)ist es notwendig, Teilchenstöße im Vakuum für schmale monoenergetische Bündel bekannter Teilchen bei vorgegebenen Stoßwinkeln zu forschen. Dabei soll die volle Forschung des Prozesses des Zusammenstoßes die Prüfung des Gleichgewichts der Energien von Teilchen (für jeden Streuwinkel im Raum), die Prüfung des Gleichgewichts von Teilchenimpulsen, die Prüfung des Gleichgewichts der Gesamtzahl von Teilchen im Bündel vor und nach dem Zusammenstoß (Wahrscheinlichkeit von Zerstreuung), die Prüfung des Gleichgewichts der entstehenden Strahlung nach Energien und Richtungen in sich einschließen. Es gibt noch zwei Fragen, auf die gewöhnlich die Aufmerksamkeit nicht gelenkt wird (noch zwei Unbestimmtheiten): ob die Zerstreuung von der gegenseitigen Orientierung eigener Drehungsmomente der zusammenstoßenden Teilchen abhängt? Ob sich eigene Drehungsmomente im Prozess des Zusammenstoßes ändern? In der klassischen Physik ist die Antwort auf diese Fragen bestätigend (in quantitativer Hinsicht hängt sie stark vom „Aufbau“ der Kügelchen ab).
Der Autor traf keine volle Analyse irgendwelchen Prozesses des Zusammenstoßes in der SRT laut den oben aufgezählten Punkten. Daraus folgt keine eindeutige Schlussfolgerung von Ungenauigkeit (in Grenzen von experimentellen Fehlern) der relativistischen gewöhnlich angewendeten Erhaltungssätze im beliebigen Prozess des Zusammenstoßes (obwohl es in vielen Einzelfällen ganz so sein kann). Der Autor besteht nur darauf, dass sogar einzelne Beispiele der absoluten Bestätigung der relativistischen Gesetze der Zusammenstöße (geschweige denn die werbende globale Nachweisbarkeit) nicht existieren.
Die Anwendung der relativistischen Erhaltungssätze zum Prozess des Zusammenstoßes in der Elementarteilchenphysik ist von prinzipiell strengen Positionen aus ziemlich zweifelhaft. Ob sie ihre Form unabhängig von der Ladung der zusammenstoßenden Teilchen, Stoßwinkel und Streuwinkel beibehalten können? Im Prozess des Zusammenstoßes erleiden die Teilchen doch Beschleunigung. Folglich soll gewisse Strahlung (Feld)laut den heutigen Vorstellungen (darunter in der SRT) immer beobachtet werden. Ob man wie die Studenten vorgehen soll, die die Lösung der Aufgabe abgucken: falls das Gerät das Gamma-Quant registrierte („hat uns ertappt“), soll man es offensichtlich „mit gescheiter Miene“ ins Kalkül ziehen. Und soll man in übrigen Fällen an die Richtigkeit der SRT-Formeln „mit gescheiter Miene“ glauben? Wo ist denn die „voraussagende Kraft“ der SRT? In der Tat sind die Erhaltungssätze durch die Glieder zu ergänzen, die Energie und Impuls des Feldes berücksichtigen.
Der einzige Fall, wann die Besprechung der relativistischen Erhaltungssätze bei „Zusammenstößen“ eigentlich rechtmäßig ist, ist die Wechselwirkung von Teilchen durch Kräfte elektromagnetischer Herkunft (Lorentz-Kraft). Die Erfüllung der relativistischen Erhaltungssätze in übrigen Fällen ist eine ungeprüfte Hypothese (die SRT-Lichtsphären haben mit den Kräften der nicht elektromagnetischen Herkunft nichts zu tun). Aber auch im Fall mit elektromagnetischen Wechselwirkungen braucht man keine SRT-Ideen für die Ableitung der relativistischen Erhaltungssätze. Es ist bekannt, dass die Bewegungsgleichungen mit Anfangsbedingungen alle Bewegungscharakteristiken, darunter Bewegungsintegrale völlig bestimmen. Als solch ein Bewegungsintegral kann Energie sein (doch nicht immer). Aus der Bewegungsgleichung folgt
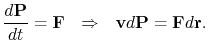 |
(4.8) |
Führen wir die Bestimmung von Potentialenergie ein
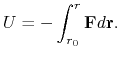
Die Art des Impulses wissend (das ist die Größe, die in die experimentelle Bewegungsgleichung(4.8) eingeschlossen ist), z.B., im klassischen Fall
im relativistischen
kann man den Energieerhaltungssatz von
ableiten: entsprechend das klassische
oder relativistische
Unter der Bedingung der Gleichheit von Wirkungs-und Gegenwirkungskräften (das
dritte Gesetz von Newton, Hypothese der Zentralkräfte) haben wir: ![]() . Darauf kann man von der Bewegungsgleichung (4.8) den
Impulserhaltungssatz (das ist die Größe wieder, die in die experimentelle
Bewegungsgleichung(4.8) eingeschlossen ist) erhalten: aus
. Darauf kann man von der Bewegungsgleichung (4.8) den
Impulserhaltungssatz (das ist die Größe wieder, die in die experimentelle
Bewegungsgleichung(4.8) eingeschlossen ist) erhalten: aus ![]() erhalten wir
erhalten wir
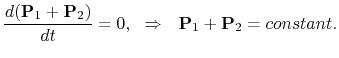
Beim Vorhandensein von Magnetkräften ![]() kann auch der relativistische Impulserhaltungssatz von Teilchen
im allgemeinen Fall verletzt werden. Da die meisten Teilchen, sogar viele
elektrisch neutrale, das Magnetmoment haben (d.h., sie stellen nicht „ideale
SRT-Punktladungen“, sondern geladene magnetische Endmaßrotatoren dar), ist die
Anwendung des relativistischen Impulserhaltungssatzes in der Kernphysik und der
Elementarteilchenphysik ohne offenbare Erfassung des Feldimpulses völlig
unrechtmäßig. Also kommen wir wieder zur Notwendigkeit der offenbaren Erfassung
des Feldimpulses, d.h., seiner Energie, bei Zusammenstößen. (Hilft es
vielleicht, die Kernphysik und die Elementarteilchenphysik zu regeln und die
Zahl der Gespenster-Teilchen zu reduzieren?).
kann auch der relativistische Impulserhaltungssatz von Teilchen
im allgemeinen Fall verletzt werden. Da die meisten Teilchen, sogar viele
elektrisch neutrale, das Magnetmoment haben (d.h., sie stellen nicht „ideale
SRT-Punktladungen“, sondern geladene magnetische Endmaßrotatoren dar), ist die
Anwendung des relativistischen Impulserhaltungssatzes in der Kernphysik und der
Elementarteilchenphysik ohne offenbare Erfassung des Feldimpulses völlig
unrechtmäßig. Also kommen wir wieder zur Notwendigkeit der offenbaren Erfassung
des Feldimpulses, d.h., seiner Energie, bei Zusammenstößen. (Hilft es
vielleicht, die Kernphysik und die Elementarteilchenphysik zu regeln und die
Zahl der Gespenster-Teilchen zu reduzieren?).
Die Erfassung der Kraft von Strahlungsrückwirkung führt auch zur Verletzung der in der SRT erklärten Erhaltungssätze von Energie und Impuls. Soll man auf die Erfassung dieser Kraft im Prozess des Teilchenstoßes verzichten? Doch dort soll diese Kraft die bedeutendste sein (es gibt große Felder infolge der Annäherung von hochenergetischen Teilchen und große variable Beschleunigungen).
Artecha S.N.