La teoría de las colisiones y las leyes de la conservación en la TER

Muy frecuentemente en la TER para la "simplificación" de la descripción de las colisiones se utiliza el método de transición a algún sistema de referencia "que se mueva comodamente". Pero tal procedimiento no tiene ninguna base física el principio de relatividad para los sistemas idénticos cerrados no tiene absolutamente nada que ver aquí. Si se realizan experimentos relativistas con haces de partículas artificiales, entonces las fuentes (los aceleradores) y los aparatos registradores están atados a la Tierra y ni los aceleradores ni lo aparatos saldrán volando de nuestra imágen mental con un observador en movimiento. Si se estudia cierto proceso en la cámara de Wilson, las trazas de las partículas estarán atadas al medio (es dedir, a la cámara de Wilson) y no al observador en vuelo. Por ejmplo, en la física clásica el ángulo entre las trazas de las partículas no cambia a causa del movimiento del observador. Al mismo tiempo, el ángulo entre las velocidades de las partículas que dejan las trazas indicadas puede depender de la velocidad de movimiento del observador. En la física relativista los ángulos entre las trayectorias y entre las velocidades de las partículas también depende según diversas leyes de la velocidad de movimiento del observador. Por eso tal transición, de aspecto al parecer verosímil desde el punto de vista de la TER, hacia un nuevo sistema de referencia puede deformar considerablemente la interpretación de la solución, es decir, cualquier proceso debe estudiarse sólo en el sistema del observador real (del aparato registrador).

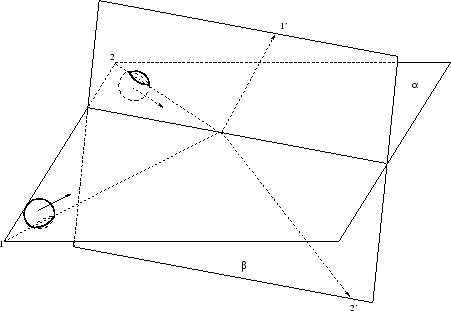
Otra distorsión de la realidad lo es el estudio del proceso de colisión de dos partículas (categóricamente puntuales en la TER) como un movimiento plano. En realidad, incluso durante la investigación de las características estáticas de partículas puntuales el aparato medidor no puede (para el ajuste al problema ideal del movimiento de dos puntos) volar con cada par de partículas y girar a su modo (¡de otra manera!): la posición del aparato está fija. Además, las partículas puntuales se deben analizar como el caso límite de las partículas de dimensiones reales finitas, de otro modo no se observaría ningún choque, no se podrían estudiar las colisiones de los átomos y las moléculas, los protones no tendrían estructura, etc. Y en este caso la colisión de las partículas es un caso escencialmente tridimensional (la probabilidad del movimiento plano es igual a cero). Supongamos, por ejemplo, que dos bolas iguales (1 y 2) se acercan una a la otra hasta colisionar por dos rectas que se cruzan en el espacio (la distancia mínima entre las rectas es menor que el diámetro de una bola). Ya desde el inicio de este experimento no podemos trazar un plano a través de estas rectas. Aún así, tomemos el centro de la distancia mínima entre las rectas que se cruzan (entre las trayectorias hasta el choque) y tracemos a través de él rectas que se intersectan, paralelas a las trayectorias dadas.

Figura 4.8: El movimiento no-plano de dos partículas.

Ahora pasa un plano único $\alpha$ a través de las rectas que se intersectan (Fig. 4.8). Los centros de las bolas se mueven hasta el momento de la colisión paralelamente a este plano: el centro de la primera bola se mueve un poco más arriba del plano y el centro de la segunda bola un poco más abajo de este plano. Después de la colisión, las bolas volarán por otras rectas que se cruzan. Nuevamente no se puede trazar un plano a través de estas rectas. Realizamos otra vez un procedimiento análogo con la transposición paralela de las rectas sobre las que yacen las líneas de movimiento después de la colisión hasta que se intersecten en el centro. Tracemos un plano $\beta$ a través de las rectas que se intersectan (nuevamente los centros de las bolas se moverán en diferentes lados de este plano). Sin embargo, " el plano antes de la colisión" no coincide con " el plano después de la colisión" y lo intersecta formando un cierto ángulo con él.

Segunda forma: tracemos un plano $\gamma$ a través de la trayectoria de movimiento de la primera partícula (las rectas de su movimiento antes y después de la colisión y que se intersectan) y un segundo plano $\delta$ a través de la segunda trayectoria análoga del movimiento de la segunda partícula. Empero, estos planos también se intersectan bajo un cierto ángulo (Fig. 4.9).

Figura 4.9: La tridimensionalidad de la colisión de dos partículas.

¿Qué se sigue del movimiento tridimensional? En primer lugar, no todos los enlaces resultan ser lineales. Por ejemplo, incluso durante el movimiento rectilíneo uniforme de los cuerpos que se mueven por rectas quye se cruzan, la distancia entre los cuerpos resulta ser una función no lineal del tiempo. En segundo lugar, escribamos las leyes clásicas de conservación del impulso (en proyecciones) y de la energía:

$$v_{1x} + v_{2x} = v'_{1x} + v'_{2x}$$ (4.3)

$$v_{1y} + v_{2y} = v'_{1y} + v'_{2y}$$ (4.4)

$$v_{1z} + v_{2z} = v'_{1z} + v'_{2z}$$ (4.5)

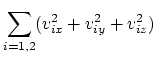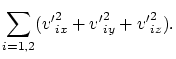$$\sum_{i=1,2}(v^2_{ix} + v^2_{iy} + v^2_{iz}) = \sum_{i=1,2}({v'}^2_{ix} + {v'}^2_{iy} + {v'}^2_{iz}).$$ (4.6)

Del sistema (4.3-4.6) vemos que para seis magnitudes desconocidas $(v'_{1x},v'_{1y},v'_{1z},v'_{2x},v'_{2y},v'_{2z})$ se tienen sólo cuatro ecuaciones. De este modo, deberán quedar dos parámetros indeterminados enla solución. Si se considera que el movimiento es plano (se quita la ecuación (4.5)), entonces tendremos tres ecuaciones para las cuatro incógnitas restantes. Luego, al comparar las soluciones de la TER con la física clásica se realiza la sustitución de las soluciones y resta solamente un parámetro indeterminado (comúnmente se considera como tal al ángulo de dispersión). Tal sustitución conduce a la interpretación errónea de los resultados del experimento, especialmente al restituir las magnitudes faltantes. Por ejemplo, en el libro [33] se muestran dos trazas del vuelo de dos partículas de igual masa y carga (¿más exactamente de igual relación $e/m$?) con un angulo de vuelo menor a $90^{\circ}$ y de auí se saca la conclusión sobre la falsedad de la mecánica clásica. Escribamos la expresión para el ángulo $\alpha$ entre las trayectorias de las particulas que se separan volando:

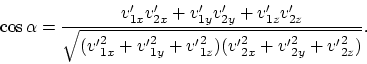$$\cos\alpha = {v'_{1x}v'_{2x} + v'_{1y}v'_{2y} + v'_{1z}v'_{2... ...1y} + {v'}^2_{1z})({v'}^2_{2x} + {v'}^2_{2y} + {v'}^2_{2z})}}.$$ (4.7)

Elijamos el eje $Z$ tal que $v_{1z}=v_{2z}=0$. Expresemos ahora la variable $v'_{1x}$ de la ecuación (4.3); la variable $v'_{1y}$, de la ecuación (4.4); la variable $v'_{1z}$, de la ecuación (4.5); y la variable ${v'}^2_{2z}$, de la ecuación (4.6) (aquí la condición ${v'}^2_{2z}>0$ limita el dominio de posibles valores de todas la variables). Sustituyamos todas las magnitudes arriba mencionadas en la ecuación (4.7). Como resultado se obtiene una dependencia biparamétrica de $v'_{2x}$ y $v'_{2y}$, la cual no escribimos a consecuencia de su comlejidad. Utilizando programas gráficos se puede uno cerciorar de que para valores dados de $v_{1x},v_{1y},v_{2x},v_{2y}$ se obtiene una cierta superficie parecida a la parte interior de un cilindro, es decir, la magnitud $\cos\alpha$ varía dentro de amplios límites. Por ejemplo, es fácil comprobar que el valor

$$v_{1x}=0,1; ~ ~ ~ v_{1y}=0,1; ~ ~ ~ v_{2x}=0,7; ~ ~ ~ v_{2y}=0,7; ~ ~ ~ v'_{1x}=0,6;$$

$$v'_{2x}=0,2; ~ ~ ~ v'_{1y}=0,4; ~ ~ ~ v'_{2y}=0,4; ~ ~ ~ -v'_{2z}=v'_{1z}=\sqrt{0,14}$$

satisface todas las leyes clásicas de conservación (4.3-4.6). Para estos valores obtenemos $\cos\alpha=0,29554$, o sea, $\alpha\approx 72,8^{\circ}$. Aclaremos: si se considera a las velocidades expresadas en unidades de la velocidad de la luz, entonces la menor velocidad es completamente real para el movimiento de los electrones internos en los átomos, iniciando con $z\ge 60$. ¡Y en general nadie ha visto electrones en reposo dentro de los átomos! El ángulo de $90^{\circ}$ se obtiene unívocamente en la física clásica durante las colisiones contra una partícula en reposo en el sistema del aparato registrador (¿pero donde encontramos tal partícula?). No obstante, del ángulo de vuelo observado igual a $90^{\circ}$ no se sigue unívocamente en absoluto la afirmación inversa sobre que una de las partículas estaba en reposo (la probabilidad matemática de tal caso es infinitamente pequeña). De esta manera, el problema inverso de restitución de los datos faltantes no es un procedimiento unívoco ni en la física clásica ni enla física relativista (existe un número infinito de soluciones distintas no contradictorias).

Para una comprobación experimental más estricta de las leyes de conservación durante las colisiones (independientemente de la teoría) es necesario estudiar las colisiones de las partículas para ángulos de colisión dados. Aquí el estudio completo del proceso de colisión deberá incluir la comprobación del balance por las energías de las partículas (para cada ángulo de dispersión en el espacio), la comprobación del balance de los impulsos de las partículas, la comprobación del balance del número total de partículas en los haces antes y después de la colisión (probabilidad de dispersión), la comprobación del balance de la radiación surgida por energías y direcciones. Hay dos preguntas más a las cuales no se presta demasiada atención (dos incertidumbres más): ¿depende la dispersión de la orientación mutua de los momentos giratorios propios de las partículas que colisionan? ¿Y cambián los momentos giratorios propios durante el proceso de la colisión? En la física clásica la respuesta a estas preguntas es afirmativa (pero en el plano cuantitativo depende fuertemente de "la construcción" de las bolas).

El autor no ha encontrado un análisis completo de algún proceso de colisión en la TER de acuerdo con todos los puntos enlistados anteriormente. De aquí no se sigue la conclusión unívoca de la falsedad (dentro de los límites de los errores experimentales) de las leyes relativistas de conservación comúnmente utilizadas en cualquier proceso de colisión (aunque en muchos casos separados esto puede ser precisamente así). El autor sólo afirma que no existen incluso ejemplos individuales de la confirmación absoluta de las leyes relativistas de las colisiones (sin hablar ya de la promovida confirmación global).

Desde una posición categóricamente estricta, la aplicaión de las leyes relativistas de conservación al proceso de colisión en la física de partículas elementales es bastante cuestionable. ¿Pueden ellas conservar su aspecto independientemente de la carga de las partículas colisionantes, de los ángulos de incidencia y de los ángulos de rebote? Ya que durante el proceso de colisión las partículas cargadas experimentan una aceleración. Luego, de acuerdo a las concepciones contemporáneas (inclusive en la TER), siempre deberá observarse cierta emisión de radiación (un campo). Acaso hay que actuar como el estudiante que espia la respuesta del problema: si el aparato registró un cuato $\gamma$ ("nos agarro de la mano"), entonces evidentemente hay que considerarlo con un " aspecto inteligente". ¿Y en el resto de los casos hay que creer con " aspecto inteligente" en la certeza de las fórmulas de la TER? ¿Dónde está pues "la capacidad de predicción" de la TER? Es evidente que en realidad a las leyes de conservación hay que agregarles aquellos miembros que consideran la energía y el impulso del campo.

Hablando en general, el único caso cuando es válido discutir las leyes relativistas de conservación para las colisiones es en el de la interacción de las partículas mediante fuerzas de naturaleza electromagnética (la fuerza de Lorenz). Para el resto de los casos el cumplimiento de las leyes relativistas de conservación es una hipótesis no comprobada (Las esferas de luz de la TER no tienen ninguna relación con las fuerzas de naturaleza no-electromagnética). Pero, en el caso de las interacciones electromagnéticas para la deducción de las leyes relativistas de conservación no se exigen en absoluto ningunas ideas de la TER. Es sabido que las ecuaciones de movimiento con condiciones iniciales determinan completamente todas las características del movimiento, incluidas las integrales de movimiento. Una de tales integrales de movimiento puede ser la energía (pero no siempre). Ecuación de movimiento se sigue que

$${d{\bf P}\over dt} = {\bf F} ~ ~ \Rightarrow ~ ~ {\bf v}d{\bf P} = {\bf F}d{\bf r}.$$ (4.8)

Introduzcamos la definición de la energía potencial

$$U = - \int_{r_0}^r {\bf F}d{\bf r}.$$

Conociendo el aspecto del impulso (esta es la magnitud que entra en la ecuación experimental de movimiento (4.8)), por ejemplo, en el caso clásico

$${\bf P} = m{\bf v},$$

y en el caso relativista

$${\bf P} = m{\bf v}/\sqrt{1-v^2/c^2},$$

se puede obtener la ecuación de conservación de la energía de

$$dE = {\bf v}d{\bf P} - {\bf F}d{\bf r}:$$

correspondientemente la clásica

$$U + mv^2/2 = const$$

o la relativista

$$U + mc^2/\sqrt{1-v^2/c^2} = const.$$

Bajo la condición de la igualdad de las fuerzas de acción y de reacción (la tercera ley de Newton, la hipótesis de las fuerzas centrales) tenemos: ${\bf F}_{12} = - {\bf F}_{21}$. Entonces de la ecuación de movimiento (4.8) se puede obtener la ley de consrvación del impulso (nuevamente esta magnitud, que entra en la ecuación experimental de movimiento (4.8)): de $d{\bf P}_1/dt={\bf F}_{12}, d{\bf P}_2/dt={\bf F}_{21}$ obtenemos

$${d({\bf P}_1+{\bf P}_2)\over dt} = 0, ~ ~ \Rightarrow ~ ~ {\bf P}_1+{\bf P}_2=const.$$

No obstante, ante la presencia de fuerzas magnéticas ${\bf F}_{12}\ne -{\bf F}_{21}$ también la ley relativista de conservación del impulso de las partículas, en el caso general, puede violarse. Puesto que la mayoría de las partículas, incluso muchas electricamente neutrales, tienen un momento magnético (es decir, representan en sí no "las cargas puntuales ideales de la TER" sino rotadores magnéticos cargados de dimensiones finitas), entonces la aplicación de la ley relativista de conservación del impulso en la física nuclear y en la física de partículas elementales es completamente inválida sin la consideración explícita del impulso del campo. Luego, volvemos nuevamente a la necesidad de considerar explícitamente el impulso del campo, y esto significa también de la energía, durante las colisiones. (Quizá esto ayude a poner en órden a la física nuclear y a la física de partículas elementales y readuzca el número de partículas-fantasma).

La consideración de la fuerza de reacción de la radiación también conduce a la violación de las leyes de conservación de la energía y del impulso anunciadas en la TER. ¿Habrá que rechazar la consideración de esta fuerza durante el proceso de colisión de las partículas? Pues esta fuerza debar'a ser ahí la más sustancial (se tienen grandes campos a causa del acercamiento de partículas altamente energéticas y grandes aceleraciones variables).