О возможном механизме частотной зависимости

Исходя из полуклассического подхода попытаемся оценить $c(\omega)$-зависимость по аналогии с оптикой. Фактически, это одна из возможных гипотез о распространении электромагнитных колебаний в вакууме. Будем описывать вакуум как некоторую систему, состоящую из виртуальных (реально не существующих) пар "частица-античастица". В отсутствие реальных частиц виртуальные частицы никак не проявляют себя (реально не существуют) в вакууме. В области распространения света возникают колебания виртуальных пар. Распространение света может быть описано как процесс последовательного взаимодействия с виртуальными парами (колебательное возбуждение). Наибольшее влияние (колебания легко возбуждаются) оказывают наилегчайшие виртуальные электрон-позитронные пары. Поэтому учитываться будут только эти пары.

Поскольку колебания в атоме или в позитронии являются примерами колебаний реальных частиц, они не могут определять собственную частоту колебаний виртуальных пар. Имеется единственная частота, которая может соответствовать виртуальной (не существующей без возбуждения) паре. Собственная частота может быть определена как частота, соответствующая рождению электрон - позитронной пары $\omega_0=2m_ec^2/\hbar$, где $m_e$ - масса электрона. При таком описании разумно предположить, что электрон и позитрон в виртуальной паре локализованы в одной и той же точке (пара реально не существует - полная аннигиляция). Используя классическую модель осцилляторов, можно записать следующее выражение для фазовой скорости света:

$$c(\omega) = {c_0\over\sqrt{\varepsilon}}, ~~~~~~ \sqrt{\varepsilon} = n - i\chi,$$ (B.1)

$$n^2 - \chi^2 = 1 + 4\pi {Nfe^2/m_e\over (\omega_0^2-\omega^2)^2 + 4\omega^2\gamma^2}(\omega_0^2-\omega^2),$$

$$n\chi = 4\pi {Nfe^2/m_e\over (\omega_0^2-\omega^2)^2 + 4\omega^2\gamma^2}\omega\gamma.$$

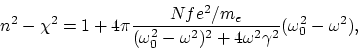
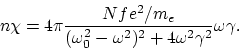
Остается определить величины $c_0$, $\gamma$ и $Nf$. При выборе величины $\gamma$ сомнений не возникает: она определяется торможением излучением (единственно возможный выбор в вакууме):

$$\gamma = {e^2\omega^2\over 3m_ec^3}.$$

При этом мы можем исследовать только те области, где классическая электродинамика внутренне непротиворечива и еще несущественны квантовые эффекты, то есть $\omega\ll\omega_0/137$ и $\lambda\gg 3.7\times 10^{-11}$ см $\gg R_0$, где $R_0=e^2/(m_{e}c^2)$ - радиус электрона. Величина $Nf$ означает такое число виртуальных пар в единице объема, которое достаточно для обеспечения процесса распространения света. Фактически речь идет об определении размеров кванта света и количества виртуальных частиц, задействованных в нем. Очевидно, что порядок продольных размеров кванта $l\sim\lambda$. Чтобы обеспечить непрерывность изменения полей ${\bf E}$ и ${\bf H}$ можно предположить, что "вещество" виртуальной пары "размазано" вдоль всего кванта (см. Рис. B.1) и вращается с частотой $\omega$ вокруг локальной оси (перпендикулярной к плоскости рисунка и пересекающей ось $C$).

Рисунок B.1: Распространение света как последовательная поляризация вакуума.

Область, занимаемая одной парой имеет размеры: $(2R_0,2R_0,R_l)$, где $R_l=\lambda/I$, $I$ - число "размазанных" пар. Поскольку средняя кинетическая энергия (энергия магнитного поля) равна средней потенциальной энергии (энергии электрического поля), то число $I$ можно найти из равенства $2Ie^2/(2R_0)=\hbar\omega$. Тогда

$$R_l = {2\pi ce^2\over \hbar\omega^2R_0}, ~~~~~ Nf = {\hbar\omega^2\over 8\pi ce^2R_0}.$$

Окончательное приближенное выражение для безразмерной фазовой скорости света имеет вид:

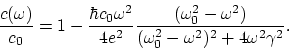$${c(\omega)\over c_{0}} = 1 - {\hbar c_{0}\omega^{2}\over 4e^... ...r (\omega_{0}^{2} - \omega^{2})^{2} + 4\omega^{2}\gamma^{2}}.$$ (B.2)

Отсюда видно, что $c_0=c(0)$. Фазовая скорость света убывает с ростом частоты.

Сделаем некоторые оценки (см.(B.2)). Для ультрафиолетовой области: $(\Delta c/c_0) \sim -0.5\times 10^{-6}$ (в видимой области эффект пренебрежимо мал). При $\omega\sim 10^{18}$ сек$^{-1}$ эффект $(\Delta c/c_0) \sim -1.4\times 10^{-5}$. Влияние движения Земли из-за эффекта Допплера вызывает даже для ультрафиолетовой области эффект $(\Delta c/c_0) \sim -10^{-10}$ (пренебрежим); а на границе области применимости данного описания ($\omega\sim\omega_0/137$) имеем: $(\Delta c/c_0) \sim -3.6\times 10^{-7}$. Используя выражение $c^2k^2=\omega^2\varepsilon$, для групповой скорости $U_g=(d\omega/dk)$ имеем:

$$U_g{d(\omega\sqrt{\varepsilon})\over d\omega} = c_0.$$

Групповая скорость также убывает с ростом частоты, практически совпадая с фазовой скоростью. Наибольшее отличие их друг от друга достигается на границе применимости данного описания (для $\omega\sim\omega_0/137$) и составляет $0.01$ процента (а в отношении к $c_0$ - порядка $2\times 10^{-7}$). Заметим также, что используемые выше малые размеры кванта света довольно обоснованы (по современным представлениям). Такой компактный объект будет взаимодействовать как целое и практически мгновенно с любым объектом микромира, а эти свойства фактически приходится постулировать в квантовой механике (например, при объяснении фотоэффекта или эффекта Комптона).

Современные общепринятые экспериментальные возможности недостаточны для определения $\omega$-зависимости скорости света в видимой области (как и влияния движения Земли). Тем не менее представим некоторые общие соображения относительно экспериментов. Необходимо поставить саму цель - обнаружить $\omega$-зависимость $c(\omega)$. Измерения должны быть прямые, поскольку любой пересчет вовлекает определенные теоретические представления о рассматриваемом процессе. В частности, эксперименты должны выполняться в вакууме, поскольку чисто теоретический расчет взаимодействия света с веществом не может быть точно выполнен. В общем случае взаимодействие с материей зависит от частоты света $\omega$. В частности, зеркала должны отражать различные по частоте $\omega$ волны по-разному (кроме того, отражение - не мгновенный процесс). Пересчет, связанный с преобразованием света не учитывает возможную $\omega$-зависимость скорости света. В общем случае, прерывание луча света изменяет волновой пакет и, следовательно, его скорость. Поскольку свободные заряженные частицы могут повлиять на эффект, необходимо избегать металлической экранировки.

Для метода прерываний необходим одновременный старт лучей с разными частотами и адекватная точность определения временных промежутков, когда волновой фронт пройдет определенное расстояние. Или, альтернативно, можно исключать спектральную линию из смеси двух спектральных линий (лазеры) с помощью прерывания. Поскольку отражение - не мгновенный процесс и зависит от частоты света, стандартная практика удлинения пути с помощью зеркал совершенно не подходит, либо же число отражений для каждого луча света (для каждой различной частоты!) должно быть равным. Последнее замечание применимо также к интерферометрическому методу. Разделяем луч ($\omega_1$) на два луча. Первый луч преобразуется (в $\omega_2$) в начале пути $L$, а второй луч - в конце пути $L$. Путь $L$ может изменяться. Если существует зависимость $c(\omega)$, то интерференционная картина должна меняться с изменением $L$. Однако, имеются технические трудности изменения $L$ без возмущений.

Астрономические исследования для довольно широкого спектра $\omega_i$ могут помочь обнаружить $c(\omega)$-зависимость. Можно наблюдать со спутника несинхронное появление и исчезновение спектральных характерных форм в двойных системах во время полного затмения. Однако, для больших расстояний нет полной уверенности, что свет действительно проходит через вакуум (без газа, плазмы, пыли и т.д.). Необходим дополнительный математический анализ $c(\omega_i)$ для $\omega_i$, чтобы обнаружить $\omega$-зависимость $c(\omega)$.

Наибольший интерес представляет сравнение $c(\omega)$ для видимой области и для рентгеновских или $\gamma$-лучей. Насколько известно, для этих областей нет экспериментальных данных. Однако, для экспериментов с $\gamma$-лучами имеется ряд трудностей (см. [7,59,67] для наиболее точного при волновой модели света метода прямых независимых измерений $\lambda$ и $\nu$), да и нет полной уверенности в чисто волновой природе света.

Наиболее общий вопрос данного приложения звучит так: остаются ли свойства вакуума неизменными при внесении в него частиц (фотонов) или нет. Если свойства вакуума изменяются, тогда должно быть и обратное влияние (принцип взаимодействия) на процесс распространения частиц (света). Зависимость $c(\omega)$ - это некоторое проявление данного принципа.

Таким образом, в приложениях были выведены соответствующие формулы для следствий $c(\omega)$-зависимости, относящиеся к СТО, квантовой электродинамике, оптике и т.д.. Для обнаружения самого факта $c(\omega)$-зависимости нужны целенаправленные исследования. Максимальный эффект должен наблюдаться для высокочастотной области. Несмотря на серьезные экспериментальные трудности, возможные результаты принципиально важны и интересны.

Здесь обсуждался один из возможных механизмов, приводящий к $c(\omega)$-зависимости для волновой модели света, но напомним, что не существует критических экспериментов, опровергающих классический закон сложения скоростей даже для корпускулярной модели света, не говоря уже о волновой модели. Дело в том, что для света следующие три зависимости являются однозначно взаимосвязанными в волновой модели света : $c(\omega)$-зависимость, закон Допплера и закон сложения скоростей. Только знание любых двух из этих зависимостей однозначно определяет третью. Для волновой модели процесс распространения электромагнитных колебаний (света) в вакууме может быть описан как последовательное возникновение колебаний виртуальных частиц (пар), вызываемое самим распространяющимся светом. (Правда, для рассмотренной в этом приложении модели возникает вопрос об различиях в свойствах света, возникающих при аннигиляции более тяжелых частиц, и роли иных виртуальных пар или об "элементарности" элементарных частиц).