Next: О возможном механизме частотной зависимости Up: Аннотация Previous: Выводы к Главе 4 Содержание
В Приложениях будет рассмотрено несколько частных гипотез. Они практически не связаны с критикой теории относительности, изложенной в основной части книги, разве что демонстрируют неединственность подхода СТО и возможность частотной параметризации всех выкладок. В данной книге Приложения только на это и претендуют, поскольку используют неверные методы СТО (их ошибочность доказана в основных главах книги). С идеями, изложенными в первых двух приложениях (плюс часть анализа опыта Майкельсона из Главы 3), автор пытался пробиться в несколько общеизвестных журналов с 1993 по 1999 год. Работа либо дипломатично не рассматривалась сразу, либо приходил примерно такой ответ: "Никто ничего подобного не обнаружил в теории относительности и квантовой электродинамике, а точность предсказаний этих теорий огромна". Как вообще теоретик может что-либо обнаружить новое (а не объяснять "задним числом")? Он должен предположить некоторый факт и проверить следствия из своего предположения. Но никто и не пытался предположить возможность зависимости скорости света от частоты. К тому же речь шла о точности на один-два порядка превышающей современную точность экспериментов. Такая точность может быть достигнута в ближайшее время, а ведь в физике серьезно обсуждаются эксперименты, требующие точности на несколько десятков порядков выше современной. Наконец, автору надоело тратить время и он решил проверить, что же это за такая великая точность теории относительности (заодно вспомнив свою студенческую неудовлетворенность этой теорией). В результате появилась первая из собственных критических статей, а теперь и эта книга. Так что во всем есть свои плюсы и минусы.
Перейдем теперь к обсуждению возможной зависимости скорости света от частоты.
Известно, что при внесении частиц в вакуум в нем происходят различные процессы,
такие как появление виртуальных пар (частица-античастица); многие процессы
взаимодействия могут быть описаны с использованием таких виртуальных пар. В
процессе своего распространения свет также влияет на свойства вакуума (в
частности, должна иметь место поляризация вакуума). Следовательно, по принципу
взаимности должно быть обратное действие поляризованного вакуума на процесс
распространения света. В результате свет определенной частоты будет
распространяться через вакуум как "среду" с некоторой проницаемостью ![]() , детерминируемой самим распространяющимся
светом, то есть
, детерминируемой самим распространяющимся
светом, то есть ![]() .
.
Известно, что обобщение уравнений Максвелла путем явного
добавления массового члена в максвелловский лагранжиан приводит к уравнениям
Прока в пространстве Минковского (по современным представлениям). Электромагнитные волны, распространяющиеся в
среде, изменяются ею и это влияние выражается в генерации массивных фотонов
[100]. Даже в предположении постоянства фазовой скорости
возникает частотная зависимость (дисперсия в вакууме) групповой скорости света:
здесь ![]() - масса покоя фотонов. В данных приложениях,
однако, не будут обсуждаться вопросы генерации массы и теории заряда. Основная
цель - отразить некоторые физические вопросы, касающиеся самой скорости света.
- масса покоя фотонов. В данных приложениях,
однако, не будут обсуждаться вопросы генерации массы и теории заряда. Основная
цель - отразить некоторые физические вопросы, касающиеся самой скорости света.
Сразу возникают вопросы: 1) Как может быть оценена или измерена ![]() -зависимость? 2) Почему она до сих пор не обнаружена, и 3)
Каковы могут быть следствия из нее?
-зависимость? 2) Почему она до сих пор не обнаружена, и 3)
Каковы могут быть следствия из нее?
Существуют различные методы измерения скорости света, например:
астрономические методы, метод прерывания, метод вращающегося зеркала,
радиогеодезический метод, метод стоячих волн (резонатор), метод независимых
измерений ![]() и
и ![]() . В настоящее время
последний из методов [59,67] является наиболее точным; именно этим методом Бюро
Стандартов измеряет скорость света с точностью до восьмого
знака. Однако, на этом пути существуют принципиальные трудности [7]. Кроме того,
следует отметить, что данный метод принципиально ограничен: он может быть связан
либо с локальной (внутри прибора) скоростью света, либо может не иметь
совершенно никакого отношения к скорости света, если свет вообще не является
чистой волной. Почему другие методы неадекватны (для обнаружения
. В настоящее время
последний из методов [59,67] является наиболее точным; именно этим методом Бюро
Стандартов измеряет скорость света с точностью до восьмого
знака. Однако, на этом пути существуют принципиальные трудности [7]. Кроме того,
следует отметить, что данный метод принципиально ограничен: он может быть связан
либо с локальной (внутри прибора) скоростью света, либо может не иметь
совершенно никакого отношения к скорости света, если свет вообще не является
чистой волной. Почему другие методы неадекватны (для обнаружения ![]() зависимости) ясно из предыдущих глав и для одной частной
гипотезы будет прояснено дальше из настоящих Приложений.
зависимости) ясно из предыдущих глав и для одной частной
гипотезы будет прояснено дальше из настоящих Приложений.
Далее мы будем следовать методам СТО (забудем на время, что они неверны, а дают лишь
эффект видимости для двух систем отсчета при дополнительном условии -
условии выбора метода синхронизации Эйнштейна).
Напомним, что при выводе следствий СТО (например, законов преобразования)
используется понятие интервала ![]() . Здесь необходимо сделать два методических замечания.
Во-первых, даже равенство интервалов
. Здесь необходимо сделать два методических замечания.
Во-первых, даже равенство интервалов ![]() - это не
более, чем одна из правдоподобных гипотез, так как достоверной остается
единственная точка
- это не
более, чем одна из правдоподобных гипотез, так как достоверной остается
единственная точка ![]() (если предполагать
(если предполагать ![]() ). Например, можно было бы приравнивать любые
). Например, можно было бы приравнивать любые
![]() -е степени (
-е степени (![]() - натуральное):
- натуральное): ![]() и получать различные "физические законы". Или же считать
и получать различные "физические законы". Или же считать ![]() , но
, но ![]() , то есть
, то есть ![]() (кажущаяся скорость взаимного движения
различна для разных наблюдателей). Такой выбор приводит к совпадению
релятивистского продольного эффекта Допплера с классическим выражением. Подобные
экзотические системы могут быть в той же степени внутренне согласованными, что и СТО
(то есть только для двух выделенных объектов!), и только эксперименты
могут продемонстрировать, какой из выборов - не более, чем теоретическое
измышление. Мы не будем обсуждать здесь все подобные экзотические гипотезы.
(кажущаяся скорость взаимного движения
различна для разных наблюдателей). Такой выбор приводит к совпадению
релятивистского продольного эффекта Допплера с классическим выражением. Подобные
экзотические системы могут быть в той же степени внутренне согласованными, что и СТО
(то есть только для двух выделенных объектов!), и только эксперименты
могут продемонстрировать, какой из выборов - не более, чем теоретическое
измышление. Мы не будем обсуждать здесь все подобные экзотические гипотезы.
Во-вторых, при использовании интервала не подчеркивается следующий момент:
используется конкретный свет, идущий из одной точки в другую, то есть в интервал
надо подставлять выражение ![]() . Но в таком случае
пропорциональность интервалов (из учебников) приводит к неопределенному
соотношению:
. Но в таком случае
пропорциональность интервалов (из учебников) приводит к неопределенному
соотношению:
и нельзя обосновать даже равенство интервалов. Опять возникает необходимость
обратиться к опыту, так как это соотношение связано с "неизвестным" пока законом
Допплера. Таким образом, теоретические построения, исходящие только из своих
собственных принципов не являются однозначными. Поскольку общепринятый вывод СТО
(метод) приводит к некоторым следствиям, якобы подтверждаемым экспериментально
(например, с некоторой точностью для динамики частиц?), будем опираться на него, но видоизменим его с
учетом возможной зависимости ![]() .
.
Физически это означает следующее. Видимый результат некоторого измерения
зависит от процедуры измерения, а расчетный результат - в частности от метода
синхронизации времени для разных систем. Согласно идее данного приложения не
существует "единой скорости передачи электромагнитных взаимодействий" (а только
![]() ). Если для синхронизации временных
интервалов согласно Эйнштейну используется свет определенной
частоты
). Если для синхронизации временных
интервалов согласно Эйнштейну используется свет определенной
частоты ![]() , то результат экспериментов будет зависеть от
, то результат экспериментов будет зависеть от
![]() . Например, если в системе происходит некоторый
процесс с характерной частотой
. Например, если в системе происходит некоторый
процесс с характерной частотой ![]() , то естественно исследовать
систему с помощью
, то естественно исследовать
систему с помощью ![]() (именно так, как и распространяется
сигнал). Если две системы движутся друг относительно друга, то в формулах
появятся две величины:
(именно так, как и распространяется
сигнал). Если две системы движутся друг относительно друга, то в формулах
появятся две величины: ![]() и
и ![]() для каждой системы, так как один и тот же свет обладает разными
частотами в системах, движущихся друг относительно друга. В этом случае величины
для каждой системы, так как один и тот же свет обладает разными
частотами в системах, движущихся друг относительно друга. В этом случае величины
![]() и
и ![]() связаны
друг с другом вследствие эффекта Допплера (смотри ниже). Интересно отметить
следующее обстоятельство. Если в системе происходят процессы с различными
характерными частотами
связаны
друг с другом вследствие эффекта Допплера (смотри ниже). Интересно отметить
следующее обстоятельство. Если в системе происходят процессы с различными
характерными частотами ![]() , то, вследствие
, то, вследствие ![]() зависимостей, движущиеся друг относительно
друга наблюдатели увидят в одной точке разные картины событий (видимый эффект).
В дальнейших выкладках мы будем следовать аналогии с [4,17].
зависимостей, движущиеся друг относительно
друга наблюдатели увидят в одной точке разные картины событий (видимый эффект).
В дальнейших выкладках мы будем следовать аналогии с [4,17].
Пусть ![]() - частота распространяющегося в системе
сигнала. Подставляя
- частота распространяющегося в системе
сигнала. Подставляя ![]() (вместо
(вместо ![]() ) в выражение интервала
) в выражение интервала ![]() для собственной системы и
для собственной системы и ![]() в
в ![]() для системы наблюдения, из
для системы наблюдения, из ![]() следует,
что собственное время(
следует,
что собственное время(![]() ) можно
определить следующим образом:
) можно
определить следующим образом:
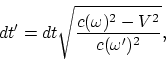 |
(A.1) |
а формула для собственной длины остается в силе. Еще раз подчеркнем, что это все - лишь "эффекты видимости". В любом математическом выражении слагаемые или коэффициенты можно по определенным правилам переносить из левой в правую часть и наоборот (все такие выражения эквивалентны). Тогда как определить: время ускорилось у одного или, наоборот, замедлилось у другого наблюдателя (а длина увеличилась или уменьшилась)? Просто, если бы Вам сказали, что Ваше время замедлилось относительно одного объекта одним образом, относительно других объектов - по-иному, то Вы бы сразу почувствовали бредовость бесконечного числа подобных бесполезных "сведений". Но когда релятивисты говорят, что у Вас все в порядке, просто "что-то у кого-то где-то далеко...", многие сразу успокаиваются и продолжают дальше слушать "сказки".
Для вывода преобразований Лоренца используем вращение
в плоскости ![]() :
:
Тогда с использованием ![]() преобразования Лоренца сводятся к
преобразования Лоренца сводятся к
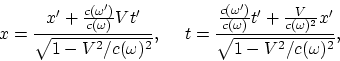 |
(A.2) |
где ![]() - скорость системы. Записывая
- скорость системы. Записывая ![]() и
и ![]() в выражении (A.2) и находя
в выражении (A.2) и находя ![]() , получаем преобразования для скорости:
, получаем преобразования для скорости:
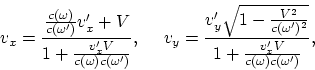
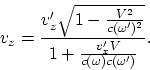 |
(A.3) |
Для движения вдоль оси ![]() имеем
имеем
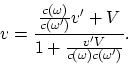 |
(A.4) |
Видно, что максимальная видимая скорость будет ![]() ,
где
,
где ![]() - частота света в собственной системе.
Заметим, что все формулы приводят к корректному закону композиции при движении
вдоль прямой (преобразования от системы
- частота света в собственной системе.
Заметим, что все формулы приводят к корректному закону композиции при движении
вдоль прямой (преобразования от системы ![]() к
к ![]() и от
и от ![]() к
к ![]() дает тот же
результат, что и преобразование от
дает тот же
результат, что и преобразование от ![]() к
к ![]() ).
Напомним, что, согласно основной части книги, величины
).
Напомним, что, согласно основной части книги, величины ![]() и
и
![]() в формулах (A.1), (A.2) не имеют
самостоятельного физического смысла (они являются фиктивными вспомогательными
величинами). Формула (A.4), по аналогии с формулой (1.5), может быть переписана в
виде
в формулах (A.1), (A.2) не имеют
самостоятельного физического смысла (они являются фиктивными вспомогательными
величинами). Формула (A.4), по аналогии с формулой (1.5), может быть переписана в
виде
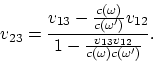 |
(A.5) |
В этой форме наиболее видна ее суть (кажущийся эффект). Формула
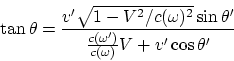 |
(A.6) |
описывает изменение направления скорости. Релятивистское выражение для аберрации
света сохраняется (подстановка ![]() ). На всякий случай напомним, что релятивистское выражение
для звездной аберрации является приближенным. Сохраняются также преобразования 4-векторов.
Отсюда следуют преобразования четырехмерного волнового вектора
). На всякий случай напомним, что релятивистское выражение
для звездной аберрации является приближенным. Сохраняются также преобразования 4-векторов.
Отсюда следуют преобразования четырехмерного волнового вектора ![]() :
:
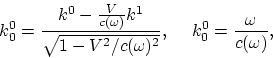
В результате получаем эффект Допплера
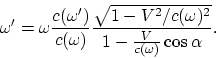 |
(A.7) |
Заметим, что отсюда следует зависимость скорости света (![]() ) от движения системы (различным системам соответствуют
различные частоты
) от движения системы (различным системам соответствуют
различные частоты ![]() ). Однако, как будет показано в
следующем приложении, этот эффект пренебрежимо мал для оптической области.
Релятивисты утверждают, что
выражение для эффекта Допплера содержит относительную скорость. Это неверно.
Пусть в некоторой точке на Земле произошел взрыв и кратковременно высветилась
некоторая линия излучения. Пусть приемник на Плутоне уловил сигнал. В какой
момент определять эту мифическую относительную скорость? Ведь в момент вспышки
приемник мог не смотреть в сторону Земли, а в момент приема сигнала уже не
существует источника, да и Земля повернулась обратной стороной. Даже в
отсутствие среды вместо относительной скорости получилась бы разница абсолютных
скоростей в момент испускания и в момент приема сигнала (а это не одно и то
же!). А что имеем в реальности - должен показать опыт.
). Однако, как будет показано в
следующем приложении, этот эффект пренебрежимо мал для оптической области.
Релятивисты утверждают, что
выражение для эффекта Допплера содержит относительную скорость. Это неверно.
Пусть в некоторой точке на Земле произошел взрыв и кратковременно высветилась
некоторая линия излучения. Пусть приемник на Плутоне уловил сигнал. В какой
момент определять эту мифическую относительную скорость? Ведь в момент вспышки
приемник мог не смотреть в сторону Земли, а в момент приема сигнала уже не
существует источника, да и Земля повернулась обратной стороной. Даже в
отсутствие среды вместо относительной скорости получилась бы разница абсолютных
скоростей в момент испускания и в момент приема сигнала (а это не одно и то
же!). А что имеем в реальности - должен показать опыт.
Вектор энергии-импульса преобразуется следующим образом:
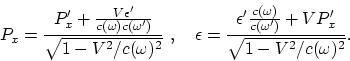 |
(A.8) |
Если следовать идее данного приложения, то должна быть более тесная аналогия между распространением света в среде и в вакууме.
(1) Различные пакеты волн расплываются в вакууме по-разному.
(2) Дисперсия света в вакууме накладывает принципиальные ограничения на степень параллельности лучей.
(3) Имеется диссипация света в вакууме, то есть интенсивность света уменьшается по мере его распространения в вакууме.
(4) Свет "стареет", то есть частота света уменьшается при распространении в вакууме. Это явление может иметь отношение к парадоксу (Ольберса) "почему небо не пылает?" и вносить свой вклад в красное смещение, то есть возможна коррекция концепции развития Вселенной. Поскольку фактически речь идет об альтернативном объяснении красного смещения, то этот эффект оказывается очень мал и подтвердить его в лабораторных исследованиях на современном этапе не представляется возможным: красное смещение линий космических объектов итак детектируется наиболее точными оптическими методами и заметным оно становится лишь для очень отдаленных объектов, таких, что расстояние до них уже не определяется даже по базе орбиты Земли (по треугольнику); напомним в этой связи, что величина постоянной Хаббла уже корректировалась на порядок.
При переходе к квантовой электродинамике во всех выкладках необходима
подстановка ![]() . Например, эта зависимость появляется в соотношении
неопределенностей
. Например, эта зависимость появляется в соотношении
неопределенностей
в условии для возможности классического описания
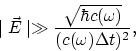
и во многих других формулах.
Существенно изменяются формулы, описывающие ![]() -зависимость. В качестве примера рассмотрим испускание и
поглощение фотонов. В результате появляется новый коэффициент
-зависимость. В качестве примера рассмотрим испускание и
поглощение фотонов. В результате появляется новый коэффициент
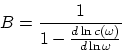
в выражении для числа фотонов ![]() заданной
поляризации:
заданной
поляризации:
и в соотношении для вероятностей (поглощения, вынужденного и спонтанного
излучения) ![]() . Величина
. Величина ![]() появляется также в
выражениях для коэффициентов Эйнштейна.
появляется также в
выражениях для коэффициентов Эйнштейна.
Используя подстановку ![]() для собственных колебаний поля, получаем
выражение для Фурье-компоненты фотонного пропагатора:
для собственных колебаний поля, получаем
выражение для Фурье-компоненты фотонного пропагатора:
Найти ![]() без явной зависимости
без явной зависимости ![]() невозможно. Явная форма
невозможно. Явная форма ![]() -зависимости
необходима также для получения окончательных выражений для различных сечений
(рассеяния, рождения пар, распада и т.д.). В качестве первого приближения можно
сделать подстановку
-зависимости
необходима также для получения окончательных выражений для различных сечений
(рассеяния, рождения пар, распада и т.д.). В качестве первого приближения можно
сделать подстановку ![]() в известных формулах.
в известных формулах.
С.Н. Артеха