Некоторые релятивистские решения и следствия

Рассмотрим парадокс преобразования сил. Пусть мы имеем два покоящихся разноименных заряда $e_1$ и $e_2$, разделенных двумя параллельными плоскостями, находящимися друг от друга на расстоянии $L$ (Рис. 4.4).

Рисунок 4.4: Парадокс преобразования сил.

Вследствие притяжения друг к другу заряды находятся на минимальном расстоянии $L$ друг от друга. (Они находятся в безразличном равновесии по отношению к системе плоскостей.) Поставим на плоскости под каждым зарядом метку или поставим рядом наблюдателей. Будем наблюдать теперь за этой системой зарядов из релятивистской ракеты, движущейся со скоростью ${\bf v}$. Пусть $\theta$ - угол между векторами ${\bf v}$ и ${\bf L}$. Определяя электромагнитные силы, действующие между этими зарядами в системе отсчета ракеты [17], будем интересоваться тангенциальными составляющими сил, т.е. компонентами сил вдоль плоскостей. На заряд $e_1$ действует сила

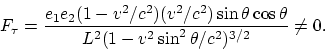$$F_{\tau} = {e_1e_2(1-v^2/c^2)(v^2/c^2)\sin\theta\cos\theta\over L^2(1-v^2\sin^2\theta/c^2)^{3/2}}\ne 0.$$ (4.1)

Следовательно, заряды сместятся из своего первоначального положения. Пусть шары будут иметь огромные заряды, $L$ будет мало ($L\rightarrow 0$), а $v$ будет велико ($v\rightarrow c$). Пусть наблюдатели удерживают шары тоненькими ниточками. Порвутся ли они? Ответ зависит от системы наблюдения. Кто же из наблюдателей прав? Таким образом, имеем очередное противоречие СТО.

Рассмотрим теперь некоторые частные задачи. Методически парадоксальным является описание движения заряженной $e$ частицы массы $m_0$ в постоянном однородном электрическом поле $E_x=E$ (см. [34]). Действительно, в классической физике траектория при $v_y=v_0$ - парабола:

$$x = eEy^2/(2m_0v_0^2),$$

а в СТО - цепная линия

$$x = {m_0c^2\over eE}\biggl ( \cosh\biggl [ {eEy\over m_0v_0c}\biggr ] - 1\biggr ).$$

Но при больших $y$ релятивистская траектория близка к экспоненте, то есть является более крутой, чем парабола. Как же быть с идеей об увеличении инерции (массы) тела со скоростью? Если даже считать, что, несмотря на несколько большую крутизну, частица движется по траектории медленнее, то за счет каких сил она замедлилась по оси $y$? Ведь сила $F_y=0$ и в СТО она тоже не появится: $F'_y=0$. Да и величина начальной скорости $v_y=v_0$ может быть нерелятивистской (и останется таковой).

Странным является баланс энергии для релятивистской ракеты [33]:

$$m\cosh\theta + M_2\cosh(d\theta) = M_1.$$

При большой скорости выброса ($\theta=\tanh(v/c)$) для конечных значений начальной $M_1$ и конечной $M_2$ масс должно быть выполнено условие: масса отдельного выброса $m\rightarrow 0$ (для непротиворечивости СТО). Однако, эта величина определяется только техническим устройством ракеты: нет принципиальных ограничений.

Один из выводов Эйнштейна соотношения $E=mc^2$ недостаточно обоснован. В этом выводе процесс поглощения телом двух симметричных импульсов света рассматривается с точки зрения двух наблюдателей, движущихся друг относительно друга. Первый наблюдатель покоится относительно тела, а второй движется перпендикулярно свету (Рис. 4.5).

Рисунок 4.5: К выводу формулы $E=mc^2$.

В СТО получается, что свет заранее должен знать о движении наблюдателя именно со скоростью $v$ и так получить импульс, чтобы в этой второй системе скорость тела не изменилась, а изменилась только его масса. Как же быть с опытами Лебедева (и современным общепринятым представлением) о давлении света, когда при передаче светом импульса изменялась именно наблюдаемая скорость тела? А что будет с импульсом, если мы будем иметь абсолютно поглощающие неровные (скошенные) поверхности? По приводимым рисункам непонятно также, имеем ли мы дело с реальным поперечным светом (моделью, принятой на сегодняшний день, в том числе и в СТО) или с мистическим продольно-поперечным светом (для спасения СТО).

Весьма странным в современной версии СТО является различие массы совокупного излучения в зависимости от импульса системы:

$$m = \sqrt{{(E_1+E_2)^2\over c^4} -{({\bf P}_1+{\bf P}_2)^2\over c^2}}.$$ (4.2)

А если мы будем менять импульс (направление) отдельных фотонов зеркалами? Будем определять при этом центр гравитации системы. Где он будет локализован и какова будет структура поля вблизи? Неужели этот центр будет скакать, исчезать и появляться вновь? Воспользуемся приведенной формулой СТО (4.2) для определения массы совокупного излучения двух фотонов, разлетающихся под произвольным углом, и рассмотрим излучение, расходящееся из одного центра (Рис. 4.6).

Рисунок 4.6: Масса комбинации фотонов.

Тогда в зависимости от попарной группировки фотонов можно получить разную совокупную массу всей системы (для "объяснения" всех возможных вариаций массы не придется ли искусственно вводить и отрицательные массы?). А в ОТО нужно учитывать предысторию рождения излучения для определения локализации его центра гравитации и учитывать всю неизвестную пространственно-временную структуру электромагнитного поля для правильного описания совершенно иного явления - гравитации. Бесконечно сложно!