Релятивистский закон сложения скоростей

Напомним, что кинематика не занимается поиском причин движения, а утверждает, например, следующее: если скорости заданы, то можно найти результат сложения скоростей. Вопросы динамики частиц (она занимается причинами движений) требуют отдельного рассмотрения (см. Главу 4).

Сделаем теперь замечание по поводу релятивистского закона сложения скоростей. Для двух систем, непосредственно участвующих в относительном движении, не возникает сомнения при определении их относительной скорости (ни в классической физике, ни в СТО). Пусть система $S_2$ движется относительно системы $S_1$ со скоростью $v_{12}$; аналогично, система $S_3$ движется относительно $S_1$ со скоростью $v_{13}$. Фактически, релятивистский закон сложения скоростей определяет относительную скорость того движения, в котором наблюдатель сам не участвует. Скорость движения системы $S_3$ относительно $S_2$ определится так:

$$v_{23} = {v_{13} - v_{12}\over 1 - {v_{13}v_{12}\over c^2}}.$$ (1.5)

Именно в таком виде (хотя обычно выражают $v_{13}$ через $v_{12}$ и $v_{23}$) раскрывается истинная суть этого закона: он говорит о том, какую относительную скорость систем $S_3$ и $S_2$ будет регистрировать наблюдатель в $S_1$, если будет пользоваться правилом Эйнштейна для синхронизации времени (с помощью световых сигналов) и измерения длин. Фактически мы опять имеем "закон видимости". (Для случая возможной параметрической зависимости скорости света от частоты это выражение будет изменено - см. Приложения.)

Рассмотрим следующее методическое замечание. Весьма странным для кинематических понятий является некоммутативность релятивистского закона сложения скоростей для неколлинеарных векторов. Свойство некоммутативности (и то, что преобразования Лоренца без вращений не составляют группу) слегка упоминается лишь в некоторых учебниках теоретической физики. Однако, например, в квантовой механике аналогичное свойство существенно меняет весь математический аппарат и физически выражает одновременную неизмеримость некоммутирующих величин.

Из общего релятивистского закона сложения скоростей

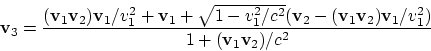$${\bf v}_3 = {({\bf v}_1{\bf v}_2){\bf v}_1/v_1^2 + {\bf v}_1... ...1{\bf v}_2){\bf v}_1/v_1^2)\over 1 + ({\bf v}_1{\bf v}_2)/c^2}$$ (1.6)

видно, что результат зависит от порядка преобразования: например, в случае последовательности

$$+v_1{\bf i}, -v_1{\bf i}, +v_2{\bf j}, -v_2{\bf j},$$

где ${\bf i}$ и ${\bf j}$ - орты прямоугольной системы координат, получаем нулевую итоговую скорость, а для другого порядка тех же величин

$$+v_1{\bf i}, +v_2{\bf j}, -v_1{\bf i}, -v_2{\bf j}$$

получим ненулевую скорость, которая весьма сложно зависит от скоростей $v_1$ и $v_2$. Последовательное применение преобразований (движений) $v_1{\bf i}$ и $v_2{\bf j}$ приводит к

$${\bf v}_3 = v_1{\bf i} + \sqrt{1-v_1^2/c^2}v_2{\bf j},$$

а в другом порядке $v_2{\bf j}$ и $v_1{\bf i}$ приводит к

$${\bf v}'_3 = v_2{\bf j} + \sqrt{1-v_2^2/c^2}v_1{\bf i},$$

то есть получаем разные вектора (Рис. 1.21).

Рисунок 1.21: Параллелограммы скоростей в СТО.

Что же в таком случае может означать разложение вектора скорости на компоненты? Во-первых, перенос простейших классических методов расчетов (коммутативной алгебры) на релятивистские уравнения (некоммутативные) неправомерен: даже решение векторных уравнений покомпонентно требует дополнительных постулатов, усложнений или разъяснений. Во-вторых, невозможно простое применение методов классической физики (принципа виртуальных перемещений, вариационных методов и т.д.). Пришлось бы даже ноль "индивидуализировать": количество "нулевых" величин, составленных из некоторой векторной комбинации должно быть равным количеству "нулевых" величин, составленных из зеркальной векторной комбинации. Следовательно, и теория флуктуаций также нуждалась бы в дополнительном обосновании. Таким образом, вопреки тезису "о простоте и элегантности СТО" для правильного обоснования даже простейших процедур пришлось бы вводить множество искусственных усложнений и разъяснений (чего нет в учебниках).

Рассмотрим логическое противоречие релятивистского закона сложения скоростей на примере одномерного случая. Пусть имеем весы, имеющие форму горизонтального желоба с горизонтальной поперечной осью посредине желоба. По желобу будут катиться два одинаковых шарика массы $m$ в разные стороны от оси (Рис. 1.22).

Рисунок 1.22: Закон сложения скоростей и противоречие весов.

Чтобы пока избежать обсуждения свойств релятивистской массы поступим так. Пусть трение оси весов отсутствует всюду, исключая точку горизонтального положения ("мертвая точка"). В этом положении порог силы трения не позволяет сдвинуться весам за счет возможной малой разности релятивистских масс (между шарами), но этот порог чувствительности не может воспрепятствовать вращению весов (с "мертвой точки") при отсутствии одного из шаров (если он упадет). Пусть скорости шаров в системе весов одинаковы по модулю. Тогда в этой системе шары одновременно докатятся до краев и упадут вниз, так что весы останутся в горизонтальном положении. Рассмотрим теперь то же движение в системе, относительно которой весы движутся со скоростью $V$. Пусть только $V \rightarrow c$, а $v \ll v_s$, где $v_s$ - скорость звука в материале желоба. Тогда весы можно считать абсолютно жесткими (игнорировать акустические волны). Согласно релятивистскому закону сложения скоростей

$$v_1 = {V-v\over 1-vV/c^2}~, ~~~~~ v_2 = {V+v\over 1+vV/c^2}~.$$

Движение средней точки со скоростью

$${v_1 + v_2\over 2} = V{1 - v^2/c^2\over 1 - v^2V^2/c^4} < V$$

всегда отстает от движения весов. Таким образом, первым свалится шарик, движущийся против направления движения весов. В результате равновесие нарушится и весы начнут вращаться. Имеем противоречие с данными первого наблюдателя. Что будет с наблюдателем, если он будет стоять под правой частью весов?

Могут ли преобразования Лоренца описывать последовательные переходы от одной инерциальной системы к другой и отвечает ли релятивистский закон сложения скоростей реальным изменениям скорости? Конечно, нет. Для начала напомним, какой смысл вкладывается в релятивистский закон сложения скоростей. Он должен доказывать, что сложение движений не может привести к скорости, большей скорости света. Как в таком случае можно складывать движения? Например, относительно звезд движется наша Земля (фактически существует первая движущаяся система отсчета), с Земли взлетает космический корабль с большой скоростью (фактически "создана" вторая движущаяся система отсчета), затем с этого космического корабля взлетает следующая ракета (третья система отсчета) и т.д.. Именно это должно иметься в виду под последовательным применением преобразований. Тогда отпадает, например, вопрос о том, какую скорость в законе сложения скоростей считать первой, а какую второй (это важно для некоммутативных преобразований). В этом смысле и приводились все примеры выше.

Рассмотрим теперь преобразования Лоренца для произвольных направлений движения:

$${\bf r}_1 = {\bf r} + {1\over V^2}\biggl ( {1\over \sqrt{1-V... ...\biggr ) ({\bf rV}){\bf V} + {{\bf V}t\over \sqrt{1-V^2/c^2}},$$

$$t_1 = {t + ({\bf rV})/c^2\over \sqrt{1-V^2/c^2}}.$$

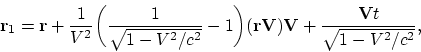
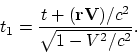
Легко проверить, что последовательное применение релятивистского закона сложения скоростей (1.6) к величинам

$$v_1{\bf i}, ~~ v_2{\bf j}, ~~ -v_1{\bf i} - v_2\sqrt{1-v_1^2/c^2}{\bf j}$$ (1.7)

дает ноль. Применим к произвольному вектору ${\bf r} = x{\bf i} + y{\bf j}$ последовательно преобразования Лоренца с тем же набором скоростей. Имеем:

$${\bf r}_1 = {x+v_1t\over \sqrt{1-v_1^2/c^2}}{\bf i} + y{\bf j},$$

$$t_1 = {t+xv_1/c^2\over \sqrt{1-v_1^2/c^2}}.$$

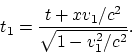
Далее имеем:

$${\bf r}_2 = {x+v_1t\over \sqrt{1-v_1^2/c^2}}{\bf i} + {y\sqr... ...xv_1v_2/c^2\over \sqrt{1-v_1^2/c^2}\sqrt{1-v_2^2/c^2}}{\bf j},$$

$$t_2 = {t+xv_1/c^2+yv_2\sqrt{1-v_1^2/c^2}/c^2\over \sqrt{1-v_1^2/c^2}\sqrt{1-v_2^2/c^2}}.$$

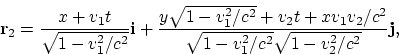
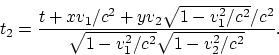
Выражения для ${\bf r}_3$ и $t_3$ не будем выписывать в явном виде ввиду их громоздкости. Однако, используя графические программы можно убедиться в следующих свойствах:
1) в новой системе начальное время десинхронизовано в любой точке пространства, кроме начала координат.
2) Промежутки времени изменились: $dt_3\ne dt$, то есть мы попали не в первоначальную покоящуюся систему, а в новую движущуюся систему. Следовательно, как минимум, в учебниках не совсем точно раскрывается смысл преобразований Лоренца или релятивистского закона сложения скоростей.
3) Отрезки оказываются не только измененной длины, но и повернутыми. В этом легко убедиться, если найти численно угол поворота, то есть разность

$$\alpha = \arctan\Biggl ( {y_3[x(1),y(1),t]-y_3[x(0),y(0),t]\over x_3[x(1),y(1),t]-x_3[x(0),y(0),t]}\Biggr ) -$$

$$- \arctan\Biggl ( {y(1)-y(0)\over x(1)-x(0)}\Biggr ) .$$

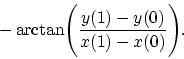
Можно сколько угодно математически объяснять эти свойства псевдоевклидовостью метрики, однако физически все просто. Эти свойства доказывают необъективный (а только кажущийся) характер преобразований Лоренца и релятивистского закона сложения скоростей и их несогласованность между собой. Действительно, поскольку мы последовательно переходили от одной инерциальной системы к другой, а поворот означает неинерциальность системы, то СТО сама выходит за рамки собственной применимости, то есть противоречива. Если бы этот поворот был реальным, то это означало бы необъективность понятия инерциальной системы (так как результат зависел бы от способа перехода к данной системе) и, как следствие, об отсутствии самой базы для существования СТО.

Попробуем разобраться, почему же трактовки из учебников приводят к несогласованности двух выражений: релятивистского закона сложения скоростей и преобразований Лоренца, несмотря на то, что первое выражение выводится из второго. Напомним этот вывод на примере одномерного взаимного движения систем $K$ и $K'$. Исходя из преобразований Лоренца

$$x_1 = {x+Vt\over \sqrt{1-V^2/c^2}}~, ~~~~ t_1 = {t+Vx/c^2\over \sqrt{1-V^2/c^2}}$$

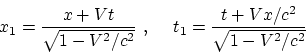
делим дифференциал $dx_1$ на $dt_1$ с учетом определений $v=dx/dt$ и $v_1=dx_1/dt_1$ и получаем:

$$v_1 = {v+V\over 1+vV/c^2}.$$

Отсюда видно следующее:
1) наблюдатель находится в центре системы $K$ и измеряет расстояние $x$ до исследуемого тела в своей системе $K$.
2) он считает время $t$ единым в своей системе и определяет скорость тела в своей системе $v=dx/dt$.
3) он измеряет скорость $-V$ системы $K'$ относительно $K$, пользуясь своим (!) временем $t$, и считает относительные скорости систем взаимно обратными по направлению. Ничего другого этот наблюдатель измерить не может: итоговая величина скорости $v_1$ является вычисляемой величиной. Таким образом, мы приходим к трактовке [49], изложенной ранее: релятивистский закон сложения скоростей определяет скорость того относительного движения, в котором сам наблюдатель не участвует. Этот эффект не реальный, а кажущийся (когда пользуемся определенными правилами СТО). По сути формулы мы не можем просто перейти ко второй подстановке для определения $v_2$, хотя формально в выражение релятивистского закона сложения скоростей можно последовательно подставлять сколько угодно величин скоростей. В случае сложения движений вдоль одной прямой классическое свойство коммутативности сохраняется и противоречие оказывается завуалированным. Но если вектора скорости неколлинеарны, то пункт 3) оказывается неверным и сразу проявляется противоречивость и несогласованность закона сложения скоростей и преобразований Лоренца.

В рассмотренном ранее примере можно поступить по-другому: будем искать последовательность трех преобразований скоростей, сохраняющую первоначальное время в преобразованиях Лоренца неизменным. Тогда легко проверить, что вместо (1.7) может быть взята единственная последовательность:

$$v_1{\bf i}, ~~ v_2{\bf j}, ~~ -v_1\sqrt{1-v_2^2/c^2}{\bf i} - v_2{\bf j} .$$ (1.8)

Однако, во-первых, поворот отрезков остается. Во-вторых, новый набор скоростей не удовлетворяет в данной последовательности закону сложения скоростей, то есть фактически поменялся порядок подстановки скоростей $v_1$ и $v_2$ в закон сложения скоростей (что не соответствует сути этого закона). Таким образом, противоречия все равно не устраняются. Одним из проявлений противоречивости СТО является прецессия Томаса: исходя из последовательности инерциальных систем (движущихся прямолинейно и равномерно) вдруг в итоге получается вращение предмета (принципиально неинерциальное движение). Таким образом, переход от излагаемых в стандартных учебниках преобразований Лоренца в "математическом пространстве" $1+1$ ($t+x$) к преобразованиям Лоренца в "пространстве" $1+2$ или $1+3$ содержит физические противоречия.

Многие интуитивно понятные свойства физических величин теряют свой смысл в СТО. Например, относительная скорость перестает быть инвариантной. Частицы, вылетающие вдоль одной прямой с разными скоростями образуют в СТО сложный "веер скоростей" для движущейся системы. Изотропное распределение по скоростям в СТО перестает быть таковым для другой движущейся системы. Никакого заявляемого упрощения в СТО на самом деле нет.

Из СТО вовсе не следует невозможность скоростей $v>c$. И добавление о том, что это относится только к скорости передачи сигнала - искусственное добавление (ввиду наличия очевидных контрпримеров к расширенному толкованию). Однако, даже с подобным добавлением остается недостаточно детерминированным понятие сигнала (информации). Например, получая сигнал от вспышки сверхновой, разве мы не уверены, что такая же информация "содержится" на диаметрально противоположном расстоянии от сверхновой, то есть мы знаем об этом со скоростью $2c$? Или это не информация? Следовательно, в СТО может иметься ввиду только информация на материальном носителе электромагнитной природы, распространяющаяся в вакууме последовательно через все точки пространства от источника до приемника сигнала.

Сделаем одно замечание по-поводу "удивительности" релятивистского закона "сложения" скоростей, позволяющего обмениваться световым сигналом, даже когда алгебраическая сумма скоростей оказывается больше $c$. Обратим внимание на очевидный факт: сигналы для обмена информацией должны посылаться обязательно в направлении объекта, а не в противоположном направлении. Поэтому нет ничего удивительного в обмене сигналов, когда и в классическом случае в результате формального сложения скоростей оказывается $v_1+v_2>v_{signal}$. Пусть два самолета взлетают с аэродрома $O$ со скоростями $0,9v_{sound}$ и разлетаются друг от друга в противоположных направлениях оси $X$ (то есть с относительной скоростью $1,8v_{sound}$). Возможен ли между ними обмен звуковыми сигналами? Разумеется! Так как звуковая волна распространяется в воздухе независимо от скорости источника $S_1$ в момент испускания сигнала, то первый самолет (пославший сигнал) будет догонять фронт волны, распространяющийся в положительном направлении оси $X$, а второй самолет будет "соревноваться" с фронтом волны, распространяющимся в отрицательном направлении оси $X$. Оба самолета движутся медленнее, чем распространяются соответствующие ближайшие к ним участки фронта волны (Рис. 1.23).

Рисунок 1.23: Обмен сигналом.

Таким образом, сумма скоростей в реальности сопоставляется (сложным образом) не со скоростью звука, а с величиной $2v_{sound}$ (а для света - с величиной $2c$).

Очевидно также, что физическое ограничение на величину скорости не может накладываться математикой (тот факт, что под знаком радикала в некоторых выражениях будет стоять отрицательная величина). Надо просто вспомнить, что все формулы СТО получены с использованием обмена световыми сигналами (метод синхронизации Эйнштейна). Если же тело сразу движется быстрее света, то его просто не сможет догнать сигнал, посланный вдогонку. Аналогично можно ввести синхронизацию с помощью звука (и также будут особенности в формулах), но отсюда вовсе не будет следовать невозможность сверхзвуковых скоростей. Скорость распространения возмущений (звуковых или световых) в среде никак не связана со скоростью движения некоторого тела сквозь эту среду.