Относительность одновременности

После критики базисного понятия времени продолжим анализ логических основ этой теории и рассмотрим вспомогательное понятие "относительность одновременности". Напомним мысленный эксперимент из СТО. Пусть по железной дороге едет поезд $A'B'$ со скоростью $v$. В полотно железной дороги ($C$) напротив центра поезда $C'$ (в момент совпадения точек $C=C'$) попадает молния. Тогда в системе, связанной с движущимся поездом, вспышка достигнет одновременно точек $A'$ и $B'$, в то время как для неподвижного наблюдателя вспышка достигнет одновременно точек $A$ и $B$ (с серединой в точке $C$), но к этому моменту точки $C$ и $C'$ (середины отрезков) разойдутся на некоторое расстояние. Однако, и в классической физике возможна подобная ситуация, если информацию из точек $A', B', A, B$ мы захотим передать в новую единую точку $D$ (или, наоборот, из точки $D$ в точки $A', B', A, B$) с некоторой конечной скоростью $v_1$ (при этом СТО и постоянство скорости света не будут играть никакой роли).

Можно предложить следующую механическую модель (Рис. 1.11).

Рисунок 1.11: Механическая модель относительности одновременности.

Пусть 4 материальные точки (без силы тяжести) "падают" со скоростью $v_1$ попарно над точкой $C$ (рядом с полотном железной дороги) и над центром поезда $C'$, который к моменту падения "подъедет" к точке $C''$ рядом с точкой $C$. Пусть в точке $C$ и в центре поезда установлены идеальные отражатели (равнобедренные треугольники с углом при основании $\alpha=\pi/4$). Тогда две частицы, отразившиеся над полотном железной дороги (в точке $C$), полетят в разные стороны со скоростью $v_1$ и одновременно достигнут точек $A$ и $B$ (в классике $\vert AB\vert=\vert A'B'\vert$). Для этого потребуется время $t=L/v_1$, где $2L$ - длина поезда. Две другие частицы, отразившиеся над центром поезда $C'$, будут двигаться относительно железной дороги со скоростями $v' = v_1+(v/\tan\alpha)=v_1+v$ вперед и $v'' = v_1-v$ назад. За то же самое время $t$ первая из этих частиц пройдет путь (вперед) $L' = v_1t+vt$, а поскольку поезд пройдет путь $vt$, то частица достигнет точки $A'$. Аналогично, для второй частицы $L'' = v_1t-vt$; следовательно, она достигнет точки $B'$. Таким образом, событие - падение точек на отражатели - будет одновременно зафиксировано во всех четырех точках: как в точках $A$ и $B$ (над железной дорогой), так и в точках $A'$ и $B'$ (над поездом). Это случай, когда точки, падающие над поездом, участвовали в его инерциальном движении. Если же вторая пара точек будет падать (над полотном железной дороги) сразу над неподвижной точкой $C''$, то треугольный отражатель у поезда (только у него) должен иметь следующие углы при основании: против движения поезда $alpha_3=0,5arctg(v1/v)$, а в направлении движения поезда $alpha_4=Pi/2-x$. В этом случае частицы полетят параллельно поезду и достигнут его концов одновременно (но не одновременно со второй парой частиц!). 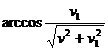Если же мы хотим, чтобы все четыре материальные точки "пролетели" одновременно над соответствующими точками $A', B', A, B$, то углы при основании отражателя (у поезда) ещё должны быть уменьшены на угол $ArcCos(v1/Sqrt(v^2+v1^2))$ (если установить плоский волновод, то пара частиц над поездом не будет "подниматься" слишком высоко, а будет двигаться параллельно поезду). Как видно, механические аналоги возможны для самых разных ситуаций.

Можно сказать, что это два разных события. Так ведь и в случае со вспышкой света (молнией) их тоже два. Действительно, пусть вспышка света происходит в момент совпадения центров $O$ и $O'$ систем $S$ и $S'$, движущихся друг относительно друга со скоростью ${\bf v}$. В некоторый момент времени $t > 0$ фронт света будет находиться на сфере $\Sigma$ относительно центра $O$ в системе $S$ и на сфере $\Sigma'$ с центром $O'$ в системе $S'$ (что кажется невозможным). Однако, ничего удивительного (противоречия с классической физикой) здесь нет, поскольку наблюдатель в системе $S$ зафиксирует свет некоторой одной частоты $\omega$, в то время как наблюдатель в системе $S'$ зафиксирует тот же свет, но другой частоты $\omega'$ (вследствие эффекта Допплера). А это уже два идентифицируемо разных события: при встрече наблюдатели всегда смогут сравнить результаты измерения $\omega$ и $\omega'$!

Разберем теперь подробнее мысленный эксперимент, "демонстрирующий" относительность одновременности: пусть вспышка света происходит в момент совпадения центров $O$ и $O'$ движущихся друг относительно друга систем $S$ и $S'$ в точке $O=O'$. Согласно СТО за время $\Delta t=t_1-t_{01}$ по часам системы $S$ свет пройдет расстояние $c(t_1-t_{01})$ от центра $O$. За такое же время $\Delta t=t_2-t_{02}$ по часам системы $S'$ тот же свет пройдет расстояние $c(t_2-t_{02})$ от центра $O'$. Согласование начальных времен не влияет на разность времен $\Delta t$ и может быть проведено как до эксперимента, так и после него любым методом. Например, можно использовать бесконечно удаленный периодический источник, расположенный перпендикулярно направлению движения. Можно заранее договориться о вспышках по часам системы $S$ (например, периодически каждый миллион лет), а систему $S'$ "организовать" за мгновение до выбранной заранее вспышки (в разделе 1.7 будет рассмотрен связанный с этим парадокс нелокальности).

Вспомним, что основная положительная идея СТО состояла в конечности скорости передачи взаимодействий. Эту же идею выражает теория близкодействия и отражает полевой подход (через уравнения Максвелла): световой фронт от источника до приемника проходит последовательно все промежуточные точки пространства. Именно с этим свойством приходит в противоречие понятие относительности одновременности (Рис. 1.12).

Рисунок 1.12: Противоречия относительности одновременности.

Для доказательства этого мы воспользуемся двумя утверждениями из СТО: 1) одна и та же вспышка света одновременно достигает движущихся друг относительно друга наблюдателей, несмотря на то, что за время прохождения света наблюдатели пространственно разойдутся друг от друга на некоторое расстояние; 2) кинематические формулы СТО (из учебников) содержат только квадрат скорости. Пусть, например, первый наблюдатель в системе $S'$ движется по направлению к источнику вспышки с малой скоростью $v\sim 10^4$ м/c. Поскольку расстояние до точки вспышки велико (миллион световых лет), то за миллион лет оба наблюдателя разойдутся на большое расстояние $\sim 2\cdot 10^{17}$ м. По формулам СТО время прихода сигнала для каждого наблюдателя будет одинаковым. В какой точке пространства первый наблюдатель "пропустил" световой фронт для второго наблюдателя? А если бы он весь миллион лет держал зеркало, а за 1 секунду до приема сигнала убрал его? По-мнению второго наблюдателя сигнал отражен первым наблюдателем где-то впереди. А что отражал первый наблюдатель, если его приборы еще не реагировали на вспышку? Аналогично, третий наблюдатель может удаляться от второго с той же скоростью, но направленной от источника. Увидит ли третий наблюдатель свет, если второй будет держать зеркало миллион лет без одной секунды?

С одной стороны, поскольку в формулы СТО входит только квадрат скорости, то второй наблюдатель будет считать одинаковым время получения сигнала первым и третьим наблюдателем. Можно договориться об отправлении без задержек дополнительно своих сигналов при получении каждым наблюдателем исследуемого сигнала. Тогда, если расчеты второго наблюдателя верны, он должен одновременно получить сигналы от первого и третьего наблюдателей (задача симметрична). Однако, с другой стороны, согласно уравнениям Максвелла свет распространяется непрерывно и второй наблюдатель получит сигнал от первого одновременно с тем, как и сам увидит исследуемый сигнал. По-мнению второго наблюдателя свет к этому времени еще не дошел до третьего наблюдателя. Таким образом, второй наблюдатель приходит в противоречие сам с собой: первые расчеты по формулам СТО противоречат вторым расчетам по уравнениям Максвелла. Очевидно, что вспышку наблюдатели увидят не одновременно, а последовательно, поскольку пространственный путь света един: источник, первый наблюдатель, затем второй, и, наконец, третий наблюдатель.

Дополнительно заметим, что даже в рамках СТО понятие относительности одновременности сильно ограничено: приложимо только к двум изолированным событиям (нет пересекающихся первопричин, нет пересекающихся последействий и, вообще, никакие дополнительные факты нас не интересуют). На самом деле, даже для этих выбранных точек световые конуса имеют пересечения, не говоря уже обо всех иных точках в пространстве и во времени. В действительности мы имеем сплошные цепи причинно связанных (и несвязанных) событий, проходящих с множеством пересечений через каждую точку пространства и времени (далеко не каждая причина вызывает наступление соответствующего следствия со скоростью света). И вся эта реальная (разномасштабная!) временная сетка взаимосвязана для всего пространства. Следовательно, в общем случае мы не можем поменять (выбором системы отсчета) порядок следования даже причинно несвязанных событий (где-то это все равно отразилось бы).