Le principe d’équivalence

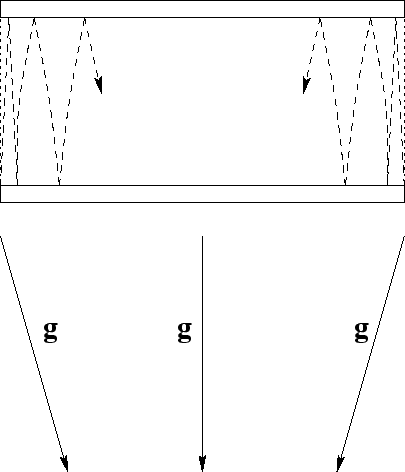
Passons à une autre notion importante de la théorie de la relativité générale - de l’équivalence du champ gravitationnel de quelque système non-à inertie. Pour distinguer des autres systèmes non-à inertie le champ gravitationnel posséde une propriété unique : tous les objets en mouvement y s'écartent vers le même centre. Si on lance deux rayons entre deux glaces idéales parallèles perpendiculairement aux miroirs, alors dans le système inértiel ils se déplaceront sans fin parallèlement l’un à l’autre. La situation analogue sera pendant l’accélération dans le système non-à inertie, si les miroirs sont orientés perpendiculairement à la direction de l’accélération. Au contraire, dans le champ gravitationnel en cas de l’orientation analogue des miroirs les rayons commeceront de se rapprocher (Figure 2.5).

Figure 2.5: Le rapprochement des rayons parallèles dans le champs gravitationnel.

Même si n’importe quel effet sera changée pendant le temps de l’observation, alors par suite d’une grande grandeur de la vitesse de lumière, la présence justement d’un champ gravitationnel (mais pas de la "sans-inértialité") aussi peut être identifiée. Il est évident qu’il ne faut pas tenir compte de la déviation des miroirs parce que outre les forces gravitationnelles il existe d’autes forces, qui peuvent retenir une configuration réciproque des miroirs. La différence de la symétrie sphèrique de celle de plate peut être établie même pour les champs gravitationnels faibles. La conclusion de la théorie de la relativité générale de la possibilité de l’exclusion du champ gravitationnel pour un certain système inértiel pendant tout le temps de l’observation en cas général est injuste.

Le principe de l’equivalence de la gravitation et de l’accélération peut être en rappots seulement avec un seul point de l’espace, c’est à dire, est irréel : cela par exemple déjà amena à un calcul incorrecte de la déflexion d’un rayon de la lumière dans le champ de gravitation (c’est seulement après que l’Einstein corrigea le coefficient en deux fois). Le principe d’équivalence d’une masse inerte et "lourde" dans la théorie de la relativité générale peut être formuler rigouresement aussi seulement pour un corps isolé (comme la théorie de la relativité générale inclut la corrélation de l’espace-temps et de tous les corps, alors il est impossible dans la théorie de la relativité générale). C’est pourquoi physiquement dans la théorie de la relativité générale ne peut pas avoir du passage limite vers aucune des théories non relativistes (mais seulement formellement mathématiquement). Toutes les transformations linéaires de la théorie de la relativité restreinte et générale se rapportent à l’espace vide, la même chose comme les corps réels (même en qualité des points repères) apportent de l’illinéalité dans les propriétés de l’espace. C’est pourquoi la différence des phénomènes en temps du passage dans un autre système de référence doit être étudiée rigouresement dans un point de l’espace et du temps. Mais comment placer dans un point de l’espace deux observateurs différents? C’est à dire tous les problèmes de la théorie de la relativité restreinte et générale peuvent avoir seulement le caractère approximatif de modèle (sans globalisation).

Il n’y a rien d’étonnant en ce que, la même grandeur - la masse - peut participer dans les phénomènes différents: comme la mesure de l’inertie en temps d’action de différentes forces, y compris celles de gravitationnelles, et comme une masse gravitationnelle (par exemple, une charge en mouvement crée le champ électrique et magnétique). La question d’égalité exacte des masses gravitationnelles et d’inertie est tout à fait tirée par les cheveux, parce que l’égalité dépend du choix de la grandeur numérique de la constant gravitationnelle $\gamma$. Par exemple, en cas de la proportion $m_g=\alpha m_{in}$ toutes les lois seront les mêmes, mais avec une autre définition d’une constant gravitationnelle $\gamma' = \alpha^2\gamma$. Il ne faut pas y chercher de la mistique et tirer les images de l’espace dévié. La substituation de la même longeur pour une masse en attraction, comme pour une masse inerte se produit non seulement dans la théorie de la relativité générale mais dans la théorie de Newton aussi. C’est tout simplement un fait expérimental (plus exactement le choix le plus simple de la grandeur $\gamma$).

Quand on parle [37], que la forme des équations dépend des propriétés de l’espace-temps, il y en a une certaine spéculation. L’impression se fait, que nous pouvons d'une manière ou d'une autre changer cet ecpase-temps pour la vérification de cette dépendance. En réalité nous avons l’univers en singulier. La tentative de la théorie de la relativité générale de compliquer n’importe quel phénomène particulier (local) par l’addition de la complexité de tout univers n’est pas positive pour la science. Une autre affaire est le choix des coordonnées locales pour la description mathématique du phénomène local (en ce cas les phénomènes concrets de symétrie simplifie la description) et le globalisme de nouveau n’y est pour rien.

L’utilisation des systèmes pas inertiels (par exemple, de la Terre) dans la théorie de la relativité générale est contradictoire à l’intérieur. Réellement, dans un système tournant les objets assez éloignés se déplaceront à la vitesse plus grande que la vitesse de la lumière, mais les théories de la relativité restreinte et générale affirment que les vitesses visibles doivent être moins que $c$. Cependant le fait expérimental: une photo du ciel de la Terre tournante montre, qu’on observe une révolution visible d’un corps dur (classique). L’utilisation d’un système tournant n’est pas contraire à la physique classique à n’importe quelle distance de l’objet du centre, en temps que dans la théorie de la relativité générale la grandeur de la composant $g_{00}$ devient négative, mais c’est inadmissible dans cette théorie. Qu’est-ce que alors faire avec les observations dans l’astronomie de la terre?