La géométrie de l’espace

La question de la possibilité du changement de la géométrie de l’espace dans la théorie de la relativité générale est tout à fait incorrecte. La finalité de la vitesse de la transmission des interactions peut changer seulement les lois physiques, mais pas mathématiques. Nous n’allons pas bien sûr affirmer que la droite n’existe pas, parce que pour la tracer dans l’infini même à la vitesse de la lumière il faudra le temps infini (analogiquement pour les plans et l’espace). Le sens mathématique des dérivées aussi ne peut pas se changer. L’une des démonstrations de la théorie de la relativité générale "de l’inévitabilité du changement de la géométrie dans un système non-à inertie" consiste en suivant: dans un système tournant de référance, par suite du racourcissement des longeurs l’attitude de la longeur de la circonférence à son diamètre sera moins que $\pi$. Remarquons que personne ne put pas encore tracer "une nouvelle géométrie" pour ce cas: il est impossible de représenter ce qui n’existe pas. En réalité non seulement une géométrie véritable, mais même une géométrie observée ne changera pas: une ligne mathématique ne se déplacera ou changera pas bien sûr pendant notre mouvement. Bien qu’en théorie de la relativité le rayon, perpendiculaire au mouvement de la circonférence, ne doit pas changer, néamoins supposons au commencement, que la circonférence se déplacera radialement. Supposons qu’on a trois circonférences concentriques du presque même rayon (Figure 2.1).

Figure 2.1: La géométrie d’une circonférence tournante.

Placeons sur eux les observateurs et numérotons les par l’ordre de centre: 1, 2, 3. Supposons que le deuxième observateur est immobile, mais le 1ème et le 3ème tournont autour le centre $O$ rotation dextrorsum et senestrorsum à une même vitesse d’angle. Alors, par suite de la différence des vitesses relatives et du raccourcissement des longeurs les observateurs s’échangeront de places. Cependant, quand ils se trouveront dans le même point de l’espace ils verront une image différente. Réellement le 1ère observateur verra la disposition suivante de centre: 3, 2, 1, en temps que le 2ème observateur verra une autre disposition: 1, 3, 2, et seulement le 3ème observateur verra une image initiale: 1, 2, 3. On a une contradiction. Supposons maintenant, que la géométrie d’un plan tournant changa. Cependant, que’est ce qui est plus préférable: le haut ou le bas? Le problème est symétrique, où est’ce que le plan se cambra? Si on va faire la dernière supposition, que le rayon se courba (de la manière comme le mouvement visible change dans le système non-à inertie), alors le deuxième observateur le verra droit, le 1ère et 3ème le trouvera "courbé" en côtés différentes. Ainsi, les trois observateurs voyons une image différente dans le même point pour le même espace, c’est à dire la déviation n’est pas objective (et ne peut pas être l’objet de l’étude scientifique).

La circonférence tournante démontre la contradiction des idées de la la théorie de la relativité restreinte et de la théorie de la relativité générale. Réellement, selon les manuels le rayon, perpendiculaire au mouvement ne changera pas. Par conséquent, les circonférences resteront à leurs places indépendamment du mouvement. Plaçons les observateurs sur une circonférence immobile equidistantement et faisons un flash pointé du centre de la circonférence, pour que les observateurs mettiont les traits sur la circonférence en mouvement en moment de l’arrivée du signal (Figure 2.2).

Figure 2.2: Les observateurs équidistants sur la circonférence.

Par suite de la symétrie du problème, les traits seront aussi équidistants. En temps des autres flashs périodiques chaque observateur confirmera, qu’en moment du flash une marque de trait passera à côté de lui (avec la périodité correspondante des flashs), c’est à dire les longeurs des parcelles d’une circonférence immobile et celles de tournantes sont égales. En cas de l’arrêt de la circonférence les marques resteront à sa place. La quantité des marques équidistantes (égale à la quantité des observateurs) ne changera pas. C’est à dire en cas immobile les longeurs des parcelles sont aussi égales. Ainsi, il n’eut pas du tout aucun raccourcissement des longeurs (et du changement de la géométrie).

Analysons maintenant la question de la géométrie de l’espace, mais de l’autre côté. Cette question est complétement embrouillée depuis l’époque de Gausse, qui voulait déterminer la géométrie à l’aide des rayons lumineux. La limité de telle ou telle expérience, elle ne peut pas donc avoir une influence sur les notions idéales mathématiques. Notons que dans la théorie de la relativité générale la lumière se déplace même pas par une ligne la plus brève: au lieu du principe de Fermat $\delta\int dl=0$ dans la la théorie de la relativité générale on a [17]: $\delta\int {(1/\sqrt{g_{00}})dl} = 0$, où $g_{\alpha\beta}$ - le tensor métrique. Par quoi est alors la lumière fut dégagée? Très souvant dans les manuels la nécessité du changement de la géométrie de la manière suivante est "justifiée": pour que la lumière tracera le triangle renfermé dans le champ gravitationnel, les miroirs deveront être tournées à un certain angle, en résultat une somme des angles du triangle se distinguera de $\pi$. Cependant pour n’importe quel corps pointé et trois réflecteurs dans le champ de la gravité (regardez Figure 2.3) on peut noter une somme des "angles":

$$\sum\beta_i = \pi + 4\arctan{\Biggl ( {gL\over 2v_0^2}\Biggr ) } - 2\arctan{\Biggl ( {gL\over v_0^2}\Biggr ) }.$$

Figure 2.3: "La géométrie du triangle".

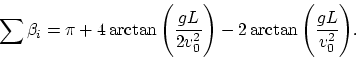
On a que la géométrie du même espace dépend des conditions de l’expérience : de $L$ et $v_0$. Comme on peut aussi changer l’angle $\alpha$ entre les glases $A$ et $B$ (sur notre image il est zéro $\alpha=0$), on reçoit la possibilité du changement factice de la géométrie en larges limites. Remarquons, que les paramètres changés $\alpha$ et $L$ restent pour la lumière aussi. Dans les démonstrations pareilles "vraisemblables" de la nécessité du changement de la géométrie quelques moments ne sont pas soulignés. Premièrement, comme dans l’expérience avec les points matériel et avec la lumière c’est la même chose la géométrie ne "se fait pas voir" en un instant, mais successivement pendant quelque temps. Deuxièmement, pour les systèmes accélérés les particules (et la lumière) se déplacent dans le vide rectilignement par la loi de l’inertie et en effect le mouvement des limites (des frontières) de ce système accélérés est mis en addition sur ce mouvement. Tous les angles de la chute (dans le système de laboratoire) sont égaux aux angles de refléction correspondants et "la géométrie des angles" ne se change pas du tout. Tout simplement, la figure se résulte d’être inrésérvé (non-close) à cause du mouvement des limites (des frontières). Troisièmement, le rôle des limites ne se révéle pas en temps de la définition des rapports des longeurs des corps réels. Par exemple, si tous les points du corps réel s'expose à l’action d’une même force accélérante, alors le rapport réciproque des longeurs et des angles ("la géométrie") reste inaltérable. Si seulement les limites s'exposent à l’accélération, alors tous les changements réels des dimentions des corps se passent seulement en interaction avec les limites. En tout cas on peut tracer les lignes droites euclidiennes. Par exemple, pour le tracement d’une ligne horizontale dans le champs gravitationnel prenons deux pivots de la même longeur (Figure 2.4).

Figure 2.4: Le tracement d’une droite dans le champs de la gravité.

Plaçons l’appui pointé pour le premier pivot au milieu d’un autre pivot. Une ligne convexe en haut se forme en résultat du courbement du pivot. Plaçons deux appuis pointés pour le deuxième pivot au niveau de deux bouts baissés du premier pivot. En résultat du courbement du deuxième pivot une ligne convexe en bas se forme. La ligne de milieu entre ses deux pivots courbés détermine une ligne droite.