Le paradoxe de la croix

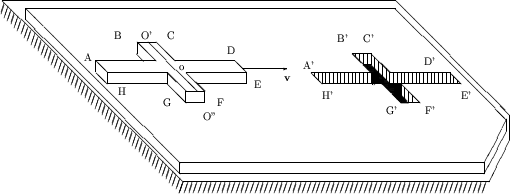
Supposons qu’une grande mince plaque de laquelle une petite croix est découpée se trouve sur un plan dur (Figure 1.15).

Figure 1.15: Le paradoxe de la croix.

Supposons que la longeur de cette croix est beaucoup plus large que la longeur d’un barreau $\vert AD\vert \gg \vert BC\vert$. Supposons que la croix glisse sur la plaque de la manière pour que, comme dans la physique classique, elle occupe sa niche (par exemple y tombe sous l’influence de la gravité). Choisissons une telle vitesse relative de mouvement $v$, pour que selon les formules de la relativité restreinte la longeur raccourcisse en deux fois (ou plus). Notons que le mouvement vertical de la croix (la chute ou le tournant du bout de devant) est possible seulement si: (1) le centre de la gravité $o$ et toute la ligne centrale du barreau ($0'0''$) se trouve au-dessus de l’espace vide, et (2) aucuns de points $C,D,E,F$ n’ont pas d’appui. Du point de vue de l’observateur sur la croix il glissera dessus la niche raccourcie en deux fois, parce que le bareau et un des bouts, ou les deux bouts s'appuient sur la plaque. Le tour célèbre avec un tournant de pivot ne réussit pas ici (nous discuterons ce problème au-dessous). Cependant, du point de vue de l’observateur la croix sur la plaque (qui devint moins en deux fois) tombera dans la niche. Alors, nous avons deux événements différents: eut-il la chute (le cognement contre le plan) ou non? Et qu’est- ce que se passera avec l’observateur se trouvant dans la niche (sera-t-il écrasé ou non)? Ou pour se sauver il doit s’accélérer d'urgence jusqu’à la vitesse de croix? Ou il doit se trouver près de la fin $A'H'$ (ou $D'E'$), où la croix raccourcie n’atteindra pas?