Possible mechanism of the frequency dependence

We shall try to evaluate the $c(\omega)$ dependence from semiclassical considerations (by analogy with optics). In fact, this is the possible hypothesis for the propagation of electromagnetic oscillations (light) in vacuum. We describe vacuum as some system consisting of virtual pairs "a particle and its antiparticle" (really not existing). In the absence of real particles, the virtual pairs do not manifest themselves (do not exist really) in vacuum. The oscillations of virtual particles arise in the region of light propagation. The light propagation can be described as a successive process of interaction with virtual pairs (oscillatory excitations). The most important influence (wherein oscillations can easily be excited) is exerted by the lightest virtual pairs (electron/positron). So, only these pairs will be taken into account here.

Since the oscillations in an atom or in a positronium are the examples of real particle oscillations, they cannot define the natural frequency of virtual pairs. There exists some unique frequency, which can be related to a virtual (not existing without excitation) pair. The natural frequency of the pair can be defined as the frequency of the electron - positron pair origin, i.e. $\omega_0=2m_ec^2/\hbar$, where $m_e$ is the electron mass. From the viewpoint of such a description, it is reasonable to assume that the electron and positron are located at the same point for a virtual pair (the pair does not really exist - the full annihilation takes place). Using the classical model of oscillators, we can write the following expression for the phase velocity of light:

$$c(\omega) = {c_0\over\sqrt{\varepsilon}}, ~~~~~~ \sqrt{\varepsilon} = n - i\chi,$$ (B.1)

$$n^2 - \chi^2 = 1 + 4\pi {Nfe^2/m_e\over (\omega_0^2-\omega^2)^2 + 4\omega^2\gamma^2}(\omega_0^2-\omega^2),$$

$$n\chi = 4\pi {Nfe^2/m_e\over (\omega_0^2-\omega^2)^2 + 4\omega^2\gamma^2}\omega\gamma.$$

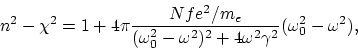
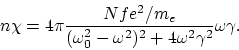
It remains to determine the quantities $c_0$,$\gamma$ and $Nf$. No doubt arises in choosing $\gamma$: this quantity is determined by the braking due to radiation (the only possible choice in vacuum). Thus,

$$\gamma = {e^2\omega^2\over 3m_ec^3}.$$

For the rest, we may study only those areas where classical electrodynamics is intrinsically non-contradictory and, besides, the quantum effects are insignificant, i.e. $\omega\ll\omega_0/137$ and $\lambda\gg 3.7\times 10^{-11}$ cm $\gg R_0$, where $R_0=e^2/(m_{e}c^2)$ is the electron radius. Quantity $Nf$ denotes the number of virtual pairs in a unit of volume, which is sufficient for providing the light propagation process. In fact, this implies the determination of the size of a quantum of light and the quantity of virtual particles acting in it. Obviously, the longitudinal size of a quantum is $l\sim\lambda$. To provide the continuity of variation of fields ${\bf E}$ and ${\bf H}$, it is necessary to suppose that the "substance" of a virtual pair be "spread out" along the whole quantum (see Fig. B.1) and rotates at frequency $\omega$ around the local axis (perpendicular to the picture plane and intersect the axis $C$).

Figure B.1: Light propagation as successive polarization of vacuum.

The region occupied by one pair has the size: $(2R_0,2R_0,R_l)$, where $R_l=\lambda/I$, $I$ is the number of "spread out" pairs. Since the mean kinetic energy (the magnetic field energy) is equal to the mean potential energy (the electric field energy), the number $I$ can be found from the equality $2Ie^2/(2R_0)=\hbar\omega$. Then

$$R_l = {2\pi ce^2\over \hbar\omega^2R_0}, ~~~~~ Nf = {\hbar\omega^2\over 8\pi ce^2R_0}.$$

The final approximate expression for the dimensionless phase velocity of light has the form:

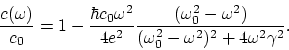$${c(\omega)\over c_{0}} = 1 - {\hbar c_{0}\omega^{2}\over 4e^... ...r (\omega_{0}^{2} - \omega^{2})^{2} + 4\omega^{2}\gamma^{2}}.$$ (B.2)

It is seen from this expression, that $c_0=c(0)$. The phase velocity of light decreases as the frequency grows.

Now we make some estimations (see (B.2)). For the ultraviolet region: $(\Delta c/c_0) \sim -0.5\times 10^{-6}$ (in the visible region the effect is negligible). For $\omega\sim 10^{18}$ s$^{-1}$ the effect is $(\Delta c/c_0) \sim -1.4\times 10^{-5}$. Even for the ultraviolet region, the influence of Earth motion via the Doppler effect causes an effect of $(\Delta c/c_0) \sim -10^{-10}$ (negligible); at the boundary of the region of applicability of this description ($\omega\sim\omega_0/137$) we have: $(\Delta c/c_0) \sim -3.6\times 10^{-7}$. Using the expression $c^2k^2=\omega^2\varepsilon$, we have for the group velocity $U_g=(d\omega/dk)$:

$$U_g{d(\omega\sqrt{\varepsilon})\over d\omega} = c_0.$$

The group velocity also decreases with frequency, virtually coinciding in magnitude with the phase velocity. The greatest difference between them occurs at the boundary of the region of applicability of this description (for $\omega\sim\omega_0/137$), and equals $0.01$ per cent (and in relation to $c_0$ - of the order of $2\times 10^{-7}$). Note, that the above-used small sizes of a light quantum are quite justified (in the modern view). Such a compact object must interact with any object of the microcosm as a whole and practically instantaneously; but, actually, these properties are postulated in quantum mechanics (in explanation of the photo-effect, or the Compton effect, for example).

The universally recognized modern experimental possibilities are inadequate for determining the $\omega$-dependence of light speed $c$ in the visible region (and its dependence on Earth motion). Nevertheless, we are presenting here general considerations concerning the experiments. To detect the $\omega$-dependent $c(\omega)$, a purposeful search is necessary. The measurements must be direct, since any recalculation invokes some theoretical concepts related to the phenomenon under consideration. In particular, the experiments must be carried out in vacuum, because purely theoretical calculations of the interaction between the light and some medium cannot be made fully. In the general case, the interaction with a matter depends on the light frequency $\omega$. Particularly, the mirror must reflect waves of different $\omega$ in a different manner (besides, reflection is not an instantaneous process). The recalculation, related with light transformations, does not take into consideration a possible $\omega$-dependence of light speed. In the general case, interruptions of light change the wave packet and, thus, its speed. Since free charged particles influence the effect, it is necessary to avoid the metallic shielding.

The method of interruptions requires simultaneous launch of the rays at different frequencies and adequate accuracy of comparison between time intervals over which the wave fronts travel a certain distance. Alternatively, one can eliminate the spectrum line from a mixture of two spectrum lines (lasers) by interruptions. Since reflections are not instantaneous effects and depend on the light frequency, the standard practice of distance lengthening by mirrors must be ruled out, or the number of reflections for each light beam (for each different $\omega$!) must be the same. The latter remark can also be applied to the interferometric method. We separate a ray ($\omega_1$) into two rays. The first is transformed into $\omega_2$ at the beginning of path $L$, and the second at the end of $L$. The path $L$ can be changed. If there exists the dependence $c(\omega)$, then the interferogram will change with $L$. However, there are some technical problems in changing $L$ without disturbances.

The astronomical research (for the rather wide spectrum $\omega_i$) can help in verifying the $c(\omega)$ dependence. One can observe (from a satellite) the (non-synchronous) appearance and disappearance of spectrum characteristic form in binary systems during the total eclipse. However, there is no confidence for large distances that the light travels through real vacuum (without gases, plasmas, dust etc.). The mathematical analysis of $c(\omega_i)$ for $\omega_i$ is necessary to detect the $\omega$-dependent $c(\omega)$.

Of utmost interest is the comparison of $c(\omega)$ for the visible region with that for X-rays or $\gamma$-rays. As far as we know, no appropriate experimental data exist for this region. However, there are some difficulties for experiments with $\gamma$-rays (see [7,59,67], for the most precise (in the wave model of light) method of direct independent measurements of $\lambda$ and $\nu$), and absolute assurance of the wave nature of light is missing.

The most general question of these Appendixes is as follows: whether or not the vacuum retains its properties regardless of the presence of particles (photons) inside it. If vacuum properties can change, then there must be an inverse action on the particles (light) propagation process (this is just the interaction principle). The $c(\omega)$ dependence is some manifestation of this principle.

Thus, in Appendixes the appropriate formulas were derived for corollaries from the $\omega$-dependence which were concerned the relativity, quantum electrodynamics, optics, etc. Purposeful experimental investigations are necessary in order to detect the fact of $c(\omega)$ dependence itself. The maximum effect must be observed for the high-frequency region. In spite of serious experimental difficulties, possible outlooks are important and promising.

One possible mechanism leading to $c(\omega)$ dependence was discussed in this Section, but recall that no critical experiments exist to disprove the classical law of velocity addition even for the corpuscular model of light, to say nothing about the wave model of light. The problem is that for light the following three relationships are uniquely interrelated (in the wave model of light): $c(\omega)$ dependence, the Doppler effect and the velocity addition law. If and only if we know any two of these relationships with certainty can the third relationship be determined uniquely. For the wave model of light, the process of the electromagnetic oscillation (light) propagation through vacuum can be described as a successive origination of oscillation of virtual particles (in pairs) induced by the propagating light itself. (However, for the considered model the questions arise about "elementary character" of elementary particles: whether light properties are different for annihilation of more heavy particles and what is the role of other virtual pairs in this process.)