Anlage B.   Vom möglichen Mechanismus der Frequenzabhängigkeit

Vom halbklassischen Herangehen ausgehend, versuchen wir die $c(\omega)$-Abhängigkeit nach Analogie mit der Optik einzuschätzen. In der Tat ist es eine von möglichen Hypothesen von der Verbreitung der elektromagnetischen Schwingungen im Vakuum. Wir werden das Vakuum als ein System beschreiben, das aus virtuellen (real nicht existierenden) Paaren „Teilchen-Antiteilchen“ besteht. Beim Fehlen der realen Teilchen zeigen sich die virtuellen Teilchen im Vakuum nicht (sie existieren real nicht). Auf dem Gebiet der Lichtfortpflanzung entstehen Schwingungen von virtuellen Paaren. Die Lichtfortpflanzung kann als Prozess der konsequenten Wechselwirkung mit virtuellen Paaren (Schwingungserregung) beschrieben werden. Den größten Einfluss (Schwingungen regen sich schnell an) üben die leichtesten virtuellen Elektron-Positron-Paare aus. Deswegen werden nur diese Paare erfasst.

Da die Schwingungen im Atom oder im Positronium als Beispiele der Schwingungen von realen Teilchen sind, können sie die Eigenfrequenz der Schwingungen von virtuellen Paaren feststellen. Es gibt eine einzige Frequenz, die dem virtuellen Paar entsprechen kann (das ohne Erregung nicht existiert). Die Eigenfrequenz kann als Frequenz bestimmt werden, die der Erzeugung des Elektron-Positron-Paares $\omega_0=2m_ec^2/\hbar$ entspricht, wo $m_e$ die Elektronmasse ist. Bei solcher Beschreibung ist es vernünftig vorauszusetzen, dass das Elektron und das Positron im virtuellen Paar in einem und demselben Punkt lokalisiert sind (das Paar existiert real nicht – die volle Annihilation). Unter Anwendung des klassischen Oszillatormodells kann man folgenden Ausdruck für die Phasenlichtgeschwindigkeit aufschreiben:

$$c(\omega) = {c_0\over\sqrt{\varepsilon}}, ~~~~~~ \sqrt{\varepsilon} = n - i\chi,$$ (B.1)

$$n^2 - \chi^2 = 1 + 4\pi {Nfe^2/m_e\over (\omega_0^2-\omega^2)^2 + 4\omega^2\gamma^2}(\omega_0^2-\omega^2),$$

$$n\chi = 4\pi {Nfe^2/m_e\over (\omega_0^2-\omega^2)^2 + 4\omega^2\gamma^2}\omega\gamma.$$

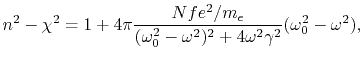
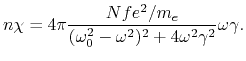
Es bleibt übrig, die Größen $c_0, \gamma$ und $Nf$ zu bestimmen. Bei der Wahl der Größe $\gamma$ entsteht kein Zweifel: sie wird durch Strahlungsbremsung bestimmt (die einzig mögliche Wahl im Vakuum):

$$\gamma = {e^2\omega^2\over 3m_ec^3}.$$

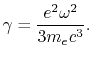
Dabei kann man nur die Gebiete erforschen, wo die klassische Elektrodynamik innerlich nicht widerspruchsvoll ist und die Quanteneffekte noch unwesentlich sind, d.h., $\omega\ll\omega_0/137$ und $\lambda\gg 3.7\times 10^{-11}$ cm, wo $R_0=e^2/(m_{e}c^2)$ der Elektronenradius ist. Die Größe $Nf$ bedeutet die Zahl der virtuellen Paare in der Volumeneinheit, die für die Sicherung der Lichtfortpflanzung genügend ist. In der Tat geht die Rede von der Bestimmung der Größe des Lichtquanten und der Zahl der virtuellen Teilchen, die in ihm betätigt sind. Es ist unverkennbar, dass die Reihenfolge der longitudinalen Größen des Quanten $l\sim\lambda$ ist. Um die Kontinuität der Veränderung der Felder ${\bf E}$ und ${\bf H}$ zu sichern, kann man voraussetzen, dass „die Substanz“ des virtuellen Paares entlang dem ganzen Quanten (s. Abb. B.1) „verschwommen“ ist und mit der Frequenz $\omega$ um die lokale Achse rotiert (senkrecht zur Abbildungsebene und überquerend die Achse $C$).

Abbildung B.1: Lichtfortpflanzung als konsequente Polarisation des Vakuums.

Der Bereich, den ein Paar besetzt, hat die Ausmaße: $(2R_0,2R_0,R_l)$, wo $R_l=\lambda/I$, $I$ die Zahl der „verschwommenen“ Paare. Da die durchschnittliche kinetische Energie (Energie des Magnetfeldes) der durchschnittlichen Potentialenergie (Energie des elektrischen Feldes) gleich ist, kann man die Zahl $I$ von der Gleichheit $2Ie^2/(2R_0)=\hbar\omega$ ableiten. Dann

$$R_l = {2\pi ce^2\over \hbar\omega^2R_0}, ~~~~~ Nf = {\hbar\omega^2\over 8\pi ce^2R_0}.$$

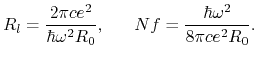
Der endgültige annähernde Ausdruck für die dimensionslose Phasenlichtgeschwindigkeit sieht so aus:

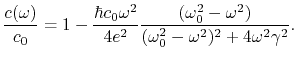$${c(\omega)\over c_{0}} = 1 - {\hbar c_{0}\omega^{2}\over 4e^{2}}{... ... \omega^{2})\over (\omega_{0}^{2} - \omega^{2})^{2} + 4\omega^{2}\gamma^{2}}.$$ (B.2)

Hier sieht man, dass $c_0=c(0)$. Die Phasenlichtgeschwindigkeit geht mit der Zunahme der Frequenz zurück.

Machen wir manche Einschätzungen (s. (B2)). Für das Ultraviolett: $(\Delta c/c_0)\sim -0.5\times 10^{-6}$ (im sichtbaren Bereich ist der Effekt unwesentlich klein). Bei $\omega\sim 10^{18}$ sek ist der Effekt $(\Delta c/c_0)\sim -1.4\times 10^{-5}$. Der Einfluss der Erdbewegung wegen dem Doppler-Effekt ruft sogar für das Ultraviolett den Effekt $(\Delta c/c_0)\sim -10^{-10}$ (unwesentlich) hervor; und an der Grenze der Anwendbarkeit der gegebenen Beschreibung ( $\omega\sim\omega_0/137$) haben wir: $(\Delta c/c_0)\sim -3.6\times 10^{-7}$. Unter Anwendung $c^2k^2=\omega^2\varepsilon$ haben wir für die Gruppengeschwindigkeit $U_g=(d\omega/dk)$:

$$U_g{d(\omega\sqrt{\varepsilon})\over d\omega} = c_0.$$

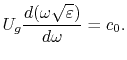
Die Gruppengeschwindigkeit geht auch mit der Zunahme der Frequenz zurück, indem sie praktisch mit der Phasengeschwindigkeit zusammenfällt. Der größte Unterschied zwischen ihnen wird an der Grenze der Anwendbarkeit der gegebenen Beschreibung (für $\omega\sim\omega_0/137$) und macht 0.01 Prozent aus (und im Verhältnis $c_0$ etwa $2\times 10^{-7}$). Bemerken wir auch, dass die oben angewendeten kleinen Lichtquantengrößen genügend begründet sind (den heutigen Vorstellungen nach). So ein kompaktes Objekt wird als ein Ganzes und praktisch blitzschnell mit beliebigem Objekt der Mikrowelt zusammenwirken, und man ist in der Tat gezwungen, diese Eigenschaften in der Quantenmechanik zu postulieren (z.B., bei der Erklärung des Photoeffektes oder des Kompton-Effektes).

Die gegenwärtigen allgemeingültigen experimentellen Möglichkeiten sind für die Bestimmung der $\omega$-Abhängigkeit der Lichtgeschwindigkeit im sichtbaren Bereich nicht ausreichend (wie auch des Einflusses der Erdbewegung ). Ungeachtet dessen stellen wir uns manche allgemeine Überlegungen betreffs Experimente vor. Es ist notwendig, selbst das Ziel zu setzen, die $\omega$-Abhängigkeit des $c(\omega)$ zu entdecken. Die Messungen sollen direkt sein, weil jede Umrechnung bestimmte theoretische Vorstellungen vom betrachtenden Prozess heranzieht. Insbesondere sollen die Experimente im Vakuum angestellt, weil die rein theoretische Berechnung der Wechselwirkung des Lichts mit der Materie exakt nicht gemacht werden kann. Im allgemeinen Fall hängt die Wechselwirkung mit der Materie von der Lichtfrequenz $\omega$ ab. Die Spiegel sollen insbesondere verschiedene Wellen der Frequenz $\omega$ nach verschieden reflektieren (außerdem ist die Reflexion kein blitzschneller Prozess.) Die Umrechnung, die mit der Lichttransformation verbunden ist, berücksichtigt die mögliche $\omega$-Abhängigkeit der Lichtgeschwindigkeit nicht. Im allgemeinen Fall verändert die Unterbrechung des Lichtstrahls das Wellenpaket und folglich seine Geschwindigkeit. Da freie geladene Teilchen den Effekt beeinflussen können, ist es notwendig, Metallabschirmung zu vermeiden.

Für die Unterbrechungsmethode sind der gleichzeitige Start der Strahlen mit verschiedenen Frequenzen und die adäquate Genauigkeit der Bestimmung der Zeitabschnitte notwendig, wenn die Wellenfront eine bestimmte Entfernung zurücklegt. Oder man kann alternativ die Spektrallinie aus der Mischung von zwei Spektrallinien (Laser) durch Unterbrechung ausschließen. Da die Reflexion kein blitzschneller Prozess ist und von der Lichtfrequenz abhängt, passt die Standardpraxis der Verlängerung des Weges mit Hilfe der Spiegel vollkommen nicht oder soll die Zahl der Reflexionen für jeden Lichtstrahl (für jede verschiedene Frequenz) gleich sein. Die letzte Bemerkung ist auch für Interferometermethode anwendbar. Wir teilen den Strahl ($\omega_1$) in zwei Strahlen. Der erste Strahl wandelt (in $\omega_2$) am Anfang der Strecke $L$, und der zweite am Ende der Strecke $L$. Die Strecke $L$ kann sich ändern. Falls die $c(\omega)$-Abhängigkeit existiert, soll sich das Interferenzbild mit der $L$-Veränderung ändern. Aber es gibt technische Schwierigkeiten der $L$-Veränderung ohne Störungen.

Astronomische Forschungen für den ziemlich breiten Spektrum $\omega_i$ können helfen, die $c(\omega)$-Abhängigkeit zu entdecken. Man kann das asynchrone Erscheinen und Verschwinden der spektralen charakteristischen Formen in Doppelsystemen während der vollen Finsternis aus dem Sputnik beobachten. Für große Entfernungen aber besteht keine völlige Sicherheit, dass das Licht wirklich durch das Vakuum geht (ohne Gas, Plasma, Staub usw.). Es ist eine zusätzliche mathematische Analyse $c(\omega_i)$ für $\omega_i$ nötig, um die $\omega$-Abhängigkeit von $c(\omega)$ zu entdecken.

Das größte Interesse stellt der Vergleich $c(\omega)$ für den sichtbaren Bereich und für die Röntgen-oder Gamma-Strahlen dar. Soweit es bekannt ist, gibt es keine experimentellen Angaben für diese Gebiete. Die Experimente mit den Gamma-Strahlen haben eine Reihe von Schwierigkeiten (s. [7, 59,67] für die höchstexakte Methode von direkten unabhängigen Messungen $\lambda$ und $\nu$ beim Wellenmodell des Lichts), es besteht ja keine volle Überzeugung von der reinen Wellenherkunft des Lichts.

Eine allgemeinere Frage der gegebenen Anlage lautet so: ob die Eigenschaften des Vakuums beim Einsatz von Teilchen (Photonen) unverändert bleiben oder nicht. Wenn sich die Eigenschaften des Vakuums ändern, soll auch die Rückwirkung (Prinzip der Wechselwirkung) auf den Prozess der Ausbreitung von Teilchen (Licht) da sein. Die Abhängigkeit $c(\omega)$ ist eine Bekundung dieses Prinzips.

Aug solche Weise wurden entsprechende Formeln, die zur SRT, Quantenelektrodynamik, Optik usw. gehören, für Folgen der $c(\omega)$-Abhängigkeit in den Anlagen abgeleitet. Das Erkennen der Tatsache der $c(\omega)$-Abhängigkeit bedarf zielgerichteter Forschungen. Der maximale Effekt soll auf dem Hochfrequenzgebiet beobachtet werden. Ungeachtet der ernsthaften experimentellen Schwierigkeiten sind mögliche Ergebnisse prinzipiell wichtig und interessant.

Hier wurde einer der möglichen Mechanismen besprochen, der zur $c(\omega)$-Abhängigkeit für das Wellenmodell des Lichts bringt, Aber wir bringen Sie drauf, dass keine kritischen Experimente gibt, die das klassische Gesetz der Geschwindigkeitsaddition sogar für das Korpuskularmodell des Lichts, geschweige denn das Wellenmodell widerlegen. Die Sache besteht darin, dass folgende drei Abhängigkeiten für das Licht eindeutig im Wellenmodell des Lichts gegenseitig verbunden sind: Die $c(\omega)$-Abhängigkeit, das Doppler-Gesetz und das Gesetz der Geschwindigkeitsaddition. Nur die Kenntnis zweier davon beliebiger Abhängigkeiten legt eindeutig die dritte fest. Für das Wellenmodell kann der Prozess der Ausbreitung der elektromagnetischen Schwingungen (Licht)im Vakuum als eine konsequente Entstehung der Schwingungen von virtuellen Teilchen (Paare) beschrieben werden, die vom fortpflanzenden Licht hervorgerufen wird. (Für das in dieser Anlage betrachtete Modell entsteht freilich die Frage von den Unterschieden der Lichteigenschaften, die bei der Annihilation schwererer Teilchen entstehen, und der Rolle mancher virtueller Paare oder von der „Einfachheit“ von Elementarteilchen).