Nächste: Vom möglichen Mechanismus Nach oben: Kurze Inhaltsangabe Vorhergehende: Schlussfolgerungen zum Kapitel 4 Inhaltsverzeichnis
In den Anlagen werden einige Einzelhypothesen erörtert. Sie sind praktisch mit der Kritik der Relativitätstheorie nicht verbunden, die im Hauptteil des Buches dargelegt ist, es sei denn, dass sie die Nichteinzigartigkeit des Herangehens an die SRT und die Möglichkeit der Frequenzparametrisierung aller Auslegungen demonstrieren. Im gegebenen Buch beanspruchen die Anlagen nur das, weil sie unrichtige SRT-Methoden anwenden (ihre Fehlerhaftigkeit wurde in den Hauptkapiteln des Buches bewiesen). Mit den Ideen, die in den ersten zwei Anlagen (plus ein Teil der Analyse des Michelson-Experimentes vom Kapitel 3), versuchte der Autor in einigen allgemeinbekannten Zeitschriften von 1993 bis 1999 durchzukommen. Die Arbeit wurde entweder diplomatisch sofort nicht betrachtet, oder wurde ungefähr solche Antwort erhalten: „Keiner hat etwas ähnliches in der Relativitätstheorie und Quantenelektrodynamik entdeckt, und die Genauigkeit der Vorhersagen dieser Theorien ist riesig“. Wie kann der Theoretiker überhaupt etwas Neues entdecken (und nicht „nachträglich“ erklären)? Er soll eine gewisse Tatsache voraussetzen und die Folgen aus seiner Voraussetzung prüfen. Keiner versuchte die Möglichkeit der Abhängigkeit der Lichtgeschwindigkeit von der Frequenz vorauszusetzen. Dabei ging es um die Genauigkeit auf eine bis zwei Größenordnungen höher als die heutige Genauigkeit von Experimenten. Solche Genauigkeit kann in der nächsten Zeit erreicht werden, und in der Physik werden die Experimente ernsthaft besprochen, die die Genauigkeit auf einige Dutzende Größenordnungen höher der gegenwärtigen erfordern. Schließlich war es dem Autor überdrüssig, Zeit zu verlieren, und er beschloss zu prüfen, was so eine große Genauigkeit der Relativitätstheorie ist (zugleich an die studentische Unzufriedenheit mit der Theorie gedacht). Als Ergebnis sind der erste von eigenen kritischen Artikeln und jetzt dieses Buch erschienen. So alles hat Vor-und Nachteile.
Gehen wir jetzt zur Besprechung der möglichen Abhängigkeit der
Lichtgeschwindigkeit von der Frequenz über. Es ist bekannt, dass verschiedene
Prozesse bei der Einführung der Teilchen in das Vakuum in ihm vor sich gehen,
solche wie das Erscheinen von virtuellen Paaren (Teilchen-Antiteilchen); viele
Wechselwirkungsprozesse können unter Anwendung solcher virtuellen Paare
beschrieben werden. Im Prozess seiner Fortpflanzung beeinflusst das Licht auch
die Vakuumeigenschaften (insbesondere soll die Polarisation des Vakuums da
sein). Folglich soll die Rückwirkung des polarisierten Vakuums auf den Prozess
der Lichtfortpflanzung nach dem Gegenseitigkeitsprinzip sein. Im Ergebnis wird
sich das Licht mit bestimmter Frequenz durch das Vakuum als „Medium“ mit
gewisser Durchdringungsfähigkeit ![]() ausbreiten, die vom fortpflanzenden Licht selbst
begrenzt wird, d.h.,
ausbreiten, die vom fortpflanzenden Licht selbst
begrenzt wird, d.h., ![]() .
.
Es ist bekannt, dass die Verallgemeinerung der Maxwell-Gleichungen durch offenbare Hinzufügung von Massenglied in das Maxwell-Lagrangian zu den Procka-Gleichungen im Minkowsky-Raum führt (den heutigen Vorstellungen nach). Die elektromagnetischen Wellen, dies sich in Medien ausbreiten, werden von ihr verändert, und dieser Einfluss drückt sich in der Generation von massiven Photonen [100] aus. Sogar in der Voraussetzung der Beständigkeit der Phasengeschwindigkeit entsteht die Frequenzabhängigkeit (Dispersion im Vakuum) von Gruppenlichtgeschwindigkeit:
hier bedeutet ![]() die Photonenruhemasse. In diesen Anlagen
werden die Fragen der Generation der Masse und die Theorie der Ladung nicht
besprochen. Das Hauptziel ist, einige physische Fragen widerzuspiegeln, die
selbst die Lichtgeschwindigkeit betreffen.
die Photonenruhemasse. In diesen Anlagen
werden die Fragen der Generation der Masse und die Theorie der Ladung nicht
besprochen. Das Hauptziel ist, einige physische Fragen widerzuspiegeln, die
selbst die Lichtgeschwindigkeit betreffen.
Es entstehen sofort die Fragen: 1) Wie kann man einschätzen oder messen die
![]() -Abhängigkeit? 2) Warum ist sie bis jetzt nicht
entdeckt worden und 3) wie können ihre Folgen sein?
-Abhängigkeit? 2) Warum ist sie bis jetzt nicht
entdeckt worden und 3) wie können ihre Folgen sein?
Es gibt verschiedene Methoden der Messung der Lichtgeschwindigkeit, z.B.,
astronomische Methoden, Unterbrechungsmethode, Methode des rotierenden Spiegels,
radiogeodätische Methode, Methode der stehenden Wellen (Resonator), Methode der
unabhängigen Messungen ![]() und
und ![]() . Gegenwärtig ist die letzte der Methoden [59,67] die höchst
exakte; eben nach dieser Methode misst das Büro für Standarde die
Lichtgeschwindigkeit mit der Genauigkeit bis zum achten Zeichen. Auf diesem Weg
gibt es aber grundsätzliche Schwierigkeiten [7]. Es sei außerdem betont, dass
die gegebene Methode grundsätzlich begrenzt ist: sie kann entweder mit lokaler
(innerhalb des Gerätes) Lichtgeschwindigkeit verbunden sein, oder kann gar
keinen Bezug auf die Lichtgeschwindigkeit haben, wenn das Licht überhaupt keine
reine Welle ist. Warum andere Methoden nicht adäquat (für das Erkennen der
. Gegenwärtig ist die letzte der Methoden [59,67] die höchst
exakte; eben nach dieser Methode misst das Büro für Standarde die
Lichtgeschwindigkeit mit der Genauigkeit bis zum achten Zeichen. Auf diesem Weg
gibt es aber grundsätzliche Schwierigkeiten [7]. Es sei außerdem betont, dass
die gegebene Methode grundsätzlich begrenzt ist: sie kann entweder mit lokaler
(innerhalb des Gerätes) Lichtgeschwindigkeit verbunden sein, oder kann gar
keinen Bezug auf die Lichtgeschwindigkeit haben, wenn das Licht überhaupt keine
reine Welle ist. Warum andere Methoden nicht adäquat (für das Erkennen der ![]() - Abhängigkeit)sind, ist es aus vorangegangenen
Kapiteln ersichtlich und wird für eine Einzelhypothese weiter in den
vorliegenden Anlagen geklärt.
- Abhängigkeit)sind, ist es aus vorangegangenen
Kapiteln ersichtlich und wird für eine Einzelhypothese weiter in den
vorliegenden Anlagen geklärt.
Ferner werden wir den SRT-Methoden folgen (vergessen wir für einige Zeit,
dass sie unrichtig sind und nur „den trügerische Effekt“ für zwei Bezugssysteme
bei der zusätzlichen Bedingung – der Bedingung der Wahl der
Einstein-Synchronisationsmethode ergeben). Es sei erwähnt, dass der Begriff des
Intervalls ![]() bei der Ableitung der SRT-Folgen (z.B.,
Transformationsgesetze) angewendet wird. Da ist es notwendig, zwei methodische
Bemerkungen zu machen. Erstens ist sogar die Gleichheit der Intervalle
bei der Ableitung der SRT-Folgen (z.B.,
Transformationsgesetze) angewendet wird. Da ist es notwendig, zwei methodische
Bemerkungen zu machen. Erstens ist sogar die Gleichheit der Intervalle ![]() nichts mehr als eine der
glaubwürdigen Hypothesen, weil der einzige Punkt
nichts mehr als eine der
glaubwürdigen Hypothesen, weil der einzige Punkt
![]() (wenn man voraussetzt
(wenn man voraussetzt ![]() ) als sicher bleibt. Man
könnte, z.B., beliebige
) als sicher bleibt. Man
könnte, z.B., beliebige ![]() -Grade (
-Grade (![]() ist natürlich) gleichsetzen:
ist natürlich) gleichsetzen: ![]() und verschiedene „physische Gesetze“ erhalten. Oder annehmen
t=t', doch
und verschiedene „physische Gesetze“ erhalten. Oder annehmen
t=t', doch ![]() ,
d.h.,
,
d.h., ![]() (die scheinbare Geschwindigkeit der gegenseitigen Bewegung ist
für verschiedene Beobachter verschieden). Solche Wahl bringt zur Koinzidenz des
relativistischen longitudinalen Doppler-Effektes mit dem klassischen Ausdruck.
Gleichartige exotische Systeme können in demselben Grad innerlich vereinbart wie
in der SRT (d.h., nur für zwei gewählte Objekte!), und nur Experimente können
demonstrieren, welche Wahl nicht mehr als das theoretische Hirngespinst ist. Wir
werden hier alle gleichartigen exotischen Hypothesen nicht erörtern.
(die scheinbare Geschwindigkeit der gegenseitigen Bewegung ist
für verschiedene Beobachter verschieden). Solche Wahl bringt zur Koinzidenz des
relativistischen longitudinalen Doppler-Effektes mit dem klassischen Ausdruck.
Gleichartige exotische Systeme können in demselben Grad innerlich vereinbart wie
in der SRT (d.h., nur für zwei gewählte Objekte!), und nur Experimente können
demonstrieren, welche Wahl nicht mehr als das theoretische Hirngespinst ist. Wir
werden hier alle gleichartigen exotischen Hypothesen nicht erörtern.
Zweitens wird folgender Moment bei Anwendung des Intervalls nicht
hervorgehoben: man wendet das konkrete Licht an, das von einem Punkt zum anderen
strahlt, d.h., man braucht den Ausdruck ![]() in das Intervall zu substituieren. In diesem Fall aber führt
die Proportionalität von Intervallen (von Lehrbüchern) zum unbestimmten
Verhältnis:
in das Intervall zu substituieren. In diesem Fall aber führt
die Proportionalität von Intervallen (von Lehrbüchern) zum unbestimmten
Verhältnis:
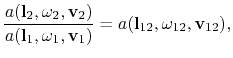
und man kann sogar die Gleichheit der Intervalle nicht begründen. Es entsteht
wieder die Notwendigkeit, sich dem Experiment zuzuwenden, da dieses Verhältnis
mit dem soweit „unbekannten“ Doppler-Gesetz verbunden ist. Auf solche Weise sind
die theoretischen Aufbauten, die nur von ihren eigenen Prinzipien ausgehen,
nicht eindeutig. Da die allgemeingültige SRT-Schlussfolgerung (Methode) zu
manchen Folgen bringt, die angeblich experimentell bestätigt werden (z.B., mit
gewisser Genauigkeit für Dynamik von Teilchen?), werden wir uns auf sie stützen,
aber wir werden sie unter Berücksichtigung der möglichen Abhängigkeit ![]() modifizieren.
modifizieren.
Physikalisch bedeutet das folgendes. Das sichtliche Resultat einer gewissen
Messung hängt vom Messungsverfahren und das Berechnungsresultat insbesondere von
der Methode der Zeitsynchronisation für verschiedene Systeme ab. Laut der Idee
der gegebenen Anlage gibt es keine „einheitliche Übertragungsgeschwindigkeit der
elektromagnetischen Wechselwirkungen“ (nur ![]() ).
Falls das Licht bestimmter Frequenz
).
Falls das Licht bestimmter Frequenz ![]() für die
Synchronisation von Zeitintervallen laut Einstein angewendet wird, wird das
Resultat von Experimenten von
für die
Synchronisation von Zeitintervallen laut Einstein angewendet wird, wird das
Resultat von Experimenten von ![]() abhängen. Wenn, z.B.,
ein gewisser Prozess mit der charakteristischen Frequenz
abhängen. Wenn, z.B.,
ein gewisser Prozess mit der charakteristischen Frequenz ![]() vor sich geht, ist es selbstverständlich, das System mit Hilfe
von
vor sich geht, ist es selbstverständlich, das System mit Hilfe
von ![]() zu
erforschen (eben so wie sich das Signal ausbreitet). Wenn sich zwei Systeme
bezüglich einander bewegen, erscheinen zwei Größen in den Formeln:
zu
erforschen (eben so wie sich das Signal ausbreitet). Wenn sich zwei Systeme
bezüglich einander bewegen, erscheinen zwei Größen in den Formeln: ![]() und
und ![]() für jedes System, weil ein und dasselbe Licht über
verschiedene Frequenzen in den bezüglich einander bewegten Systemen verfügt. In
diesem Fall sind die Größen
für jedes System, weil ein und dasselbe Licht über
verschiedene Frequenzen in den bezüglich einander bewegten Systemen verfügt. In
diesem Fall sind die Größen ![]() und
und ![]() miteinander infolge des Doppler-Effektes verbunden
(s. unten). Es ist interessant, folgenden Umstand hervortreten zu lassen. Wenn
Prozesse mit verschiedenen charakteristischen Frequenzen
miteinander infolge des Doppler-Effektes verbunden
(s. unten). Es ist interessant, folgenden Umstand hervortreten zu lassen. Wenn
Prozesse mit verschiedenen charakteristischen Frequenzen ![]() im System vor sich gehen, sehen die bezüglich einander bewegte
Beobachter infolge der
im System vor sich gehen, sehen die bezüglich einander bewegte
Beobachter infolge der ![]() -Abhängigkeiten in einem Punkt verschiedene Bilder der
Ereignisse (der trügerische Effekt). In weiteren Auslegungen werden wir den
Analogien mit [4,17]folgen.
-Abhängigkeiten in einem Punkt verschiedene Bilder der
Ereignisse (der trügerische Effekt). In weiteren Auslegungen werden wir den
Analogien mit [4,17]folgen.
Möge ![]() die Frequenz des sich im System
ausbreitenden Signals sein. Indem man
die Frequenz des sich im System
ausbreitenden Signals sein. Indem man ![]() (statt
(statt ![]() ) in den
Intervallausdruck
) in den
Intervallausdruck ![]() für das eigene System
und
für das eigene System
und ![]() in
in
![]() für das Beobachtungssystem substituiert, folgt aus
für das Beobachtungssystem substituiert, folgt aus ![]() , dass die Eigenzeit
(dr'=0) folgenderweise bestimmen kann:
, dass die Eigenzeit
(dr'=0) folgenderweise bestimmen kann:
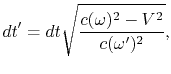 |
(A.1) |
und die Formel für die Eigenlänge bleibt in Kraft. Nochmals sei es betont, dass alles nur „trügerische Effekte“ sind. In jedem mathematischen Ausdruck kann man Summanden oder Koeffizienten nach bestimmten Regeln vom linken in den rechten Teil und umgekehrt versetzen (alle solchen Ausdrücke sind äquivalent). Wie kann man dann bestimmen: beschleunigte sich die Zeit bei einem oder umgekehrt verlangsamte sich bei dem anderen Beobachter (vergrößerte oder verkleinerte sich die Länge)? Hätte man Ihnen einfach gesagt, dass Ihre Zeit bezüglich eines Objektes auf eine Weise verlangsamte, bezüglich anderer Objekte anders, würden Sie sofort den Unsinn der endlosen Zahl gleichartiger unnützer „Informationen“ mitbekommen. Wenn die Relativisten doch sagen, dass bei Ihnen alles in Ordnung ist, aber „etwas bei jemandem weit entfernt…“, beruhigen sich viele sogleich und setzen fort, sich „die Märchen“ anzuhören.
Für die Ableitung der Lorentz-Transformationen wenden wir die Drehung in der
Ebene ![]() an:
an:
Unter Anwendung von ![]() werden dann die Lorentz-Transformationen
zusammengefasst
werden dann die Lorentz-Transformationen
zusammengefasst
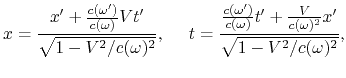 |
(A.2) |
wo ![]() die Geschwindigkeit des Systems ist. Indem wir
die Geschwindigkeit des Systems ist. Indem wir
![]() und
und ![]() im Ausdruck (A.2)
aufschreiben und
im Ausdruck (A.2)
aufschreiben und ![]() finden, bekommen wir die Transformationen
für die Geschwindigkeit:
finden, bekommen wir die Transformationen
für die Geschwindigkeit:
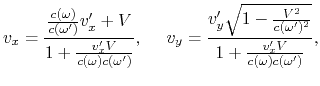
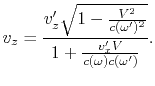 |
(A.3) |
Für die Bewegung längs der Achse ![]() haben wir
haben wir
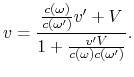 |
(A.4) |
Es ist klar, dass die maximale sichtliche Geschwindigkeit ![]() wird,wo
wird,wo ![]() die Lichtfrequenz im
eigenen System ist. Es sei bemerkt, dass alle Formeln zu einem korrekten Gesetz
der Komposition bei der Bewegung entlang der Geraden bringen (Transformationen
vom System
die Lichtfrequenz im
eigenen System ist. Es sei bemerkt, dass alle Formeln zu einem korrekten Gesetz
der Komposition bei der Bewegung entlang der Geraden bringen (Transformationen
vom System ![]() zu
zu ![]() und von
und von ![]() zu
zu ![]() ergibt dasselbe Resultat wie die
Transformation von
ergibt dasselbe Resultat wie die
Transformation von ![]() zu
zu ![]() ). Wir erinnern
Sie daran, dass die Größen t' und x' in den Formeln (A.1), (A.2)
laut dem Hauptteil des Buches keinen selbständigen Sinn tragen (sie sind fiktive
Hilfsgrößen). Die Formel (A.4), analog der Formel(1.5), kann in der Form
umgeschrieben werden
). Wir erinnern
Sie daran, dass die Größen t' und x' in den Formeln (A.1), (A.2)
laut dem Hauptteil des Buches keinen selbständigen Sinn tragen (sie sind fiktive
Hilfsgrößen). Die Formel (A.4), analog der Formel(1.5), kann in der Form
umgeschrieben werden
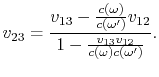 |
(A.5) |
In dieser Formel ist ihr Wesen am besten zu sehen (der scheinbare Effekt). Die Formel
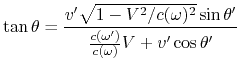 |
(A.6) |
beschreibt die Veränderung der Geschwindigkeitsrichtung. Der relativistische
Ausdruck für Lichtaberration bleibt erhalten (Substitution ![]() ).
Auf alle Fälle erinnern wir Sie daran, dass der relativistische Ausdruck für die
Sternaberration annähernd ist. Es bleiben die 4-Vektoren-Transformationen auch
erhalten. Daraus folgen die Transformationen für den vierdimensionalen
Wellenvektor
).
Auf alle Fälle erinnern wir Sie daran, dass der relativistische Ausdruck für die
Sternaberration annähernd ist. Es bleiben die 4-Vektoren-Transformationen auch
erhalten. Daraus folgen die Transformationen für den vierdimensionalen
Wellenvektor ![]() :
:
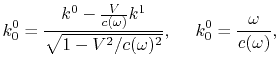
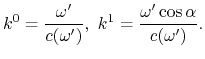
Im Ergebnis bekommen wir den Doppler-Effekt
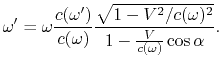 |
(A.7) |
Es sei bemerkt, dass die Abhängigkeit der Lichtgeschwindigkeit ( ![]() )
von der Bewegung des Systems daraus folgt (verschiedenen Systemen entsprechen
verschiedene Frequenzen
)
von der Bewegung des Systems daraus folgt (verschiedenen Systemen entsprechen
verschiedene Frequenzen ![]() ). Wie es doch in der
nächsten Anlage gezeigt wird, ist dieser Effekt für das optische Gebiet
unwesentlich. Die Relativisten behaupten, dass der Ausdruck für den
Doppler-Effekt die relative Geschwindigkeit enthält. Es ist unrichtig. Es
geschehe eine Explosion in einem Punkt auf der Erde, und eine Strahlungslinie
leuchtet kurzzeitig vor. Möge der Empfänger auf dem Pluto das Signal einfangen.
Im welchen Zeitpunkt soll man diese mythische relative Geschwindigkeit
feststellen? Im Zeitpunkt des Aufblitzens konnte der Empfänger nicht in der
Richtung der Erde doch schauen, im Zeitpunkt des Signalempfangens existierte die
Quelle nicht mehr, die Erde drehte sich auch mit der Rückseite um. Sogar beim
Fehlen des Mediums würde sich die Differenz der absoluten Geschwindigkeiten im
Zeitpunkt des Aussendens und im Zeitpunkt des Empfangens des Signals (und das
ist nicht dasselbe!)statt der relativen Geschwindigkeit ergeben. Was wir in der
Wirklichkeit haben, soll das Experiment zeigen.
). Wie es doch in der
nächsten Anlage gezeigt wird, ist dieser Effekt für das optische Gebiet
unwesentlich. Die Relativisten behaupten, dass der Ausdruck für den
Doppler-Effekt die relative Geschwindigkeit enthält. Es ist unrichtig. Es
geschehe eine Explosion in einem Punkt auf der Erde, und eine Strahlungslinie
leuchtet kurzzeitig vor. Möge der Empfänger auf dem Pluto das Signal einfangen.
Im welchen Zeitpunkt soll man diese mythische relative Geschwindigkeit
feststellen? Im Zeitpunkt des Aufblitzens konnte der Empfänger nicht in der
Richtung der Erde doch schauen, im Zeitpunkt des Signalempfangens existierte die
Quelle nicht mehr, die Erde drehte sich auch mit der Rückseite um. Sogar beim
Fehlen des Mediums würde sich die Differenz der absoluten Geschwindigkeiten im
Zeitpunkt des Aussendens und im Zeitpunkt des Empfangens des Signals (und das
ist nicht dasselbe!)statt der relativen Geschwindigkeit ergeben. Was wir in der
Wirklichkeit haben, soll das Experiment zeigen.
Der Energie-Impuls-Vektor wandelt sich folgenderweise um:
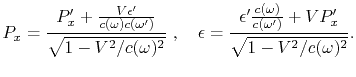 |
(A.8) |
Folgt man der Idee dieser Anlage, soll engere Analogie zwischen der Lichtfortpflanzung im Medium und im Vakuum sein.
(1) Verschiedene Wellenpakete verschwimmen im Vakuum unterschiedlich.
(2) Die Lichtdispersion im Vakuum legt prinzipielle Begrenzungen auf das Grad der Parallelität der Strahlen auf.
(3) Es gibt die Dissipation des Lichtes im Vakuum, d.h., die Intensität des Lichtes geht mit seiner Fortpflanzung im Vakuum zurück.
(4) Das Licht „altert“, d.h., die Lichtfrequenz geht mit seiner Fortpflanzung im Vakuum zurück. Diese Erscheinung kann Bezug auf das Paradoxon (von Olbers)“Warum steht der Himmel nicht in Flammen?“ haben und seinen Beitrag in die Rotverschiebung machen, d.h., es ist die Korrektion der Entwicklungskonzeption des Universums möglich. Da die Rede faktisch von der Alternativerklärung der Rotverschiebung ist, erweist sich dieser Effekt als sehr gering, und es ist unmöglich, ihn bei Laborforschungen in der gegenwärtigen Etappe zu bestätigen: die Rotverschiebung der Linien von kosmischen Objekten wird sowieso mit höchstexakten optischen Methoden nachgewiesen, und bemerkbar wird sie nur für sehr entfernte Objekte, solche, das die Entfernung bis dahin nicht mehr nach der Basis der Erdbahn (nach Dreieck)zu bestimmen ist. Es sei erwähnt, dass die Größe der Hubble-Konstante schon auf eine Größenordnung korrigiert wurde.
Beim Übergang zur Quantenelektrodynamik ist die Substitution in allen
Auslegungen von ![]() notwendig. Diese Abhängigkeit erscheint, z.B., im Verhältnis
der Unbestimmtheiten
notwendig. Diese Abhängigkeit erscheint, z.B., im Verhältnis
der Unbestimmtheiten
in der Bedingung für Möglichkeiten der klassischen Beschreibung
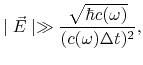
und in vielen anderen Formeln.
Wesentlich werden die Formeln verändert, die die ![]() - Abhängigkeit beschreiben. Als Beispiel betrachten wir Die
Aussendung und Absorption von Photonen. Im Ergebnis erscheint ein neuer
Koeffizient
- Abhängigkeit beschreiben. Als Beispiel betrachten wir Die
Aussendung und Absorption von Photonen. Im Ergebnis erscheint ein neuer
Koeffizient
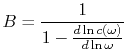
im Ausdruck für die Zahl von Photonen ![]() der vorgegebenen Polarisation:
der vorgegebenen Polarisation:
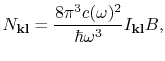
und in der Relation für Wahrscheinlichkeiten (Absorption, induzierte und
spontane Strahlung) ![]() . Die Größe
. Die Größe ![]() erscheint auch in den Ausdrücken für die Einstein-Koeffizienten.
erscheint auch in den Ausdrücken für die Einstein-Koeffizienten.
Unter Anwendung der Substitution
![]() für eigene Feldschwingungen bekommen wir den Ausdruck für die
Fourier-Komponente des Photonenpropagators:
für eigene Feldschwingungen bekommen wir den Ausdruck für die
Fourier-Komponente des Photonenpropagators:
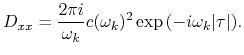
Es ist unmöglich, ![]() ohne offensichtliche
Abhängigkeit
ohne offensichtliche
Abhängigkeit ![]() zu finden. Die offensichtliche Form der
zu finden. Die offensichtliche Form der
![]() -Abhängigkeit ist auch für die Erhaltung der
endgültigen Ausdrücke für verschiedene Querschnitte notwendig (Zerstreuung,
Paarerzeugung, Zerfall usw.). Als erste Annäherung kann man die Substitution
-Abhängigkeit ist auch für die Erhaltung der
endgültigen Ausdrücke für verschiedene Querschnitte notwendig (Zerstreuung,
Paarerzeugung, Zerfall usw.). Als erste Annäherung kann man die Substitution ![]() in bekannten Formeln machen.
in bekannten Formeln machen.
Artecha S.N.