Das Machsche Prinzip

Das Machsche Prinzip der Bedingtheit von Inertialmasse und Absolutbeschleunigung durch Wirkung von fernen Sternen ist auch zweifelhaft, weil es innere Eigenschaften eines Körpers durch Eigenschaften anderer Körper erklärt. Selbstverständlich ist die Idee selbst schön. Wenn man annimmt, dass alles in der Welt in Wechselbeziehung ist und eine gewisse ideale volle Zustandsgleichung existiert, soll jede Eigenschaft von Körpern durch den Einfluss des ganzen übrigen Universums bestimmt werden. Aber dann wäre man gezwungen, jedes Teilchen für individuell zu halten. Dieser Weg ist fehlerhaft für die Wissenschaft, die sich vom wenigen Wissen zum größeren entwickelt, da "man das Unermessliche nicht fassen kann". Praktisch, wenn man die unregelmäßige Verteilung der Masse (in kompakten Objekten) und verschiedene Größen der Anziehungskräfte von den nächsten und entfernten Objekten berücksichtigen würde, sollte ein ununterbrochenes "Zerren" statt der regelmäßigen Drehung oder der regelmäßigen mechanischen Bewegung entstehen.

Grundsätzlich kann das Machsche Prinzip nicht geprüft werden: sowie die Entfernung aller Körper aus dem Universum, als auch das künstliche Richten der Gravitationskonstante nach der Null sind Abstrakta, die mit Wirklichkeit nichts zu tun haben. Aber experimentell kann man den Einfluss der "fernen Sterne" einschätzen, indem man die Masse des Universums zur hauptsächlich in kompakten Objekten konzentrierten Masse zählt. Die Anziehungskraft des Sterns mit der Masse etwa der Masse der Sonne $M\sim 2\cdot 10^{30}$ Kilogramm gleich, der sich in der Entfernung von einem Lichtjahr $\sim 9\cdot 10^{15}$ Meter befindet, ist der Wirkung der Last mit der Masse nur $m_0\sim 25$ Gramm äquivalent, die sich in der Entfernung von einem Meter befindet. Benutzen wir soweit die zweifelhafte Theorie der Großen Explosion und nehmen an, dass die Existenzzeit des Universums $\sim 2\cdot 10^{10}$ Jahre ausmacht. Sollten Sterne mit der Lichtgeschwindigkeit auseinanderfliegen, hätten wir die Dimensionen des Universums von $\sim 2\cdot 10^{10}$ Lichtjahren. Nehmen wir die mittlere Entfernung zwischen den nächsten Sternen von einem Lichtjahr an. Wir vergrößern alle Werte absichtlich, z.B., die Masse vom Universum und seine Dichte $\rho\sim 10^{33}/10^{54} \sim 10^{-21}$ g/cm$^3$. Berücksichtigen wir jetzt, dass sich die Kraft bei der Entfernung der Körper voneinander um das Doppelte auf das 4-fache reduziert usw. Versuchen wir die Einwirkungskraft des ganzen Universums in einiger Richtung zu imitieren. Hält man die mittlere Entfernung zwischen den nächsten Sternen für ein Lichtjahr, braucht man in der Entfernung von einem Meter die Masse in Gramm (summieren wir bis $2\cdot 10^{10}$)

$$M_0\sim 25(1+1/4+1/9+\cdots) = 25\sum 1/n^2\sim 25\pi^2/6 < 50$$

platzieren. Faktisch drückt der Koeffizient $\pi^2/6$ eine gewisse effektive Vergrößerung der Dichte auf der Beobachtungslinie aus. Für die Imitation der Wirkung "des ganzen Universums" kann man eine dicke Metallsphäre mit dem Außenradius von einem Meter nehmen, und die Dicke in der Richtung des Mittelpunktes variabel machen (man kann sogar für die Imitation von Inhomogenitäten eine Nadelstruktur in der Nähe des Innenradius machen).

Es soll die Dicke der ununterbrochenen Sphäre 0.6 Meter sein, d.h., vom Mittelpunkt bis 0.4 Meter eine Nische, und weiter bis zu einem Meter Metall. Dann wird das zylindrische Säulchen mit dem Radius von 0.35 cm der Masse $M_0$ bei der Dichte von 8.3 g/cm$^3$ entsprechen. In Wirklichkeit sollen wir den Einfluss der Sterne im Kegel und nicht nur im Zylinder berücksichtigen. Obwohl wir auch den kugelförmigen Metallkegel haben, schätzen wir ungeachtet dessen die Ordnungsgrößen ein. Teilen wir den Kegel in zylindrische Schichten, die infolge der Einbeziehung neuer Sternschichten entstehen (Abb. 2.9).

Abbildung 2.9: Das Machsche Prinzip und der Einfluss des Universums.

Jede neue Schicht wird um 6 Sterne größer sein, als die vorangegangene. Die Entfernungen vom Mittelpunkt bis zur nächsten Grenze jeder Sternschicht kann man aus der Ähnlichkeit von Dreiecken finden: $R_i/1 = i/r$. Dann haben wir $R'_i = \sqrt{i^2(1+r^2)}/r$. Folglich wird die Verbesserung zur Masse $M_0$ (wir summieren bis $2\cdot 10^{10}$) wie

$$m_0(1+{1\over 4}+\cdots )\biggl ( 1 + \sum_i {6\over {R'}_i^2}\biggr ) < M_0\biggl ( 1+ 6r^2 \sum_i {1\over i}\biggr )$$

$$\sim M_0\biggl ( 1 + 6 \cdot 10^{-5} \log{(2 \cdot 10^{10})}\biggr ) \sim M_0(1+0.02)$$

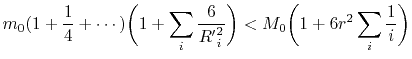
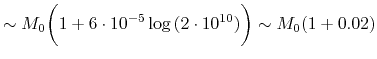
gefunden. So reicht unsere Konstruktion vollauf für die Berechnung der Wirkung des "ganzen Universums" aus. Natürlich, wenn das Universum endlos ist, wird die erhaltene harmonische Reihe auseinandergehen, und die Konstruktion wird nicht adäquat. Aber es widerspricht sowie der ART als auch den heutigen Vorstellungen und Beobachtungsangaben.

Legen wir in das Innere der Sphäre gefederte Kügelchen. Zur Vermeidung von Nebeneffekten kann man die Luft aus der Konstruktion evakuieren und die Kügelchen zusätzlich von der Sphäre durch ein dünnes Gefäß isolieren. Beginnt man die Sphäre zu drehen, soll die Schwungkraft laut dem Machschen Prinzip aufkommen, und die Kügelchen gehen auseinander. Dabei soll die Schwungkraft genau so, als ob sich selbst die Kügelchen drehen. Es scheint ganz klar zu sein, dass es unmöglich ist, da so ein Effekt längst bemerkt wäre. Auf solche Weise kehren wir zu den absoluten Begriffen von Beschleunigung, Masse, Raum und Zeit zurück, die noch von Newton bestimmt wurden. Aber das beschriebene Experiment könnte nützlich für die Bestimmung der Verbesserungen zum statischen Gravitationsgesetz von Newton sein. Dabei sollen sich die Kügelchen genug frei bewegen und drehen, weil die Wirkungsrichtung der Verbesserungskräfte und der Kraftmomente im Voraus nicht bekannt ist.