Geometrie des Raumes

Die Frage über die Möglichkeit die Veränderung der Geometrie des Raumes in der ART ist vollkommen unkorrekt. Die Endlichkeit der Übertragungsgeschwindigkeit von Wechselwirkungen kann nur physische und nicht mathematische Gesetze verändern. Wir werden doch nicht behaupten, dass die Gerade nicht existiert, weil die unendliche Zeit für ihre Ziehung in die Unendlichkeit sogar mit der Lichtgeschwindigkeit erforderlich sein wird (analog für Ebene und Raum). Der mathematische Sinn von Ableitungen kann sich auch nicht ändern. Eine der Demonstrationen der ART "über die Unvermeidlichkeit der Veränderung der Geometrie im Nichtinertialsystem" besteht im Folgenden: das Verhältnis der Länge des Kreises zu seinem Durchmesser wird im rotierenden Bezugssystem infolge der Kürzung von Längen kleiner $\pi$ sein. Es sei bemerkt, dass niemand für den gegebenen Fall eine "neue Geometrie" aufzeichnen konnte: es ist unmöglich, das Nichtexistierende darzustellen. In Wirklichkeit wird sich nicht nur die echte, sondern auch die beobachtete Geometrie nicht ändern: die mathematische Linie wird sich bei unserer Bewegung nicht bewegen oder ändern. Obwohl sich der Radius in der Relativitätstheorie, der senkrecht zur Bewegung des Kreises liegt, nicht ändern soll, vermuten wir zunächst nichtsdestoweniger, dass sich der Kreis radial bewegen wird. Mögen wir drei konzentrische Kreise fast vom gleichen Radius (Abb. 2.1) haben.

Abbildung 2.1: Geometrie des rotierenden Kreises.

Platzieren wir auf ihnen Beobachter und numerieren sie der Reihe nach vom Mittelpunkt: 1, 2, 3. Der zweite Beobachter soll ruhend sein, der 1. und der 3. Rotieren um den Mittelpunkt $O$ nach und gegen den Uhrzeigersinn mit identischer Winkelgeschwindigkeit. Dann tauschen die Beobachter ihre Plätze infolge des Unterschiedes zwischen den relativen Geschwindigkeiten und der Kürzung der Längen. Wenn sie in einem Punkt des Raumes sind, sehen sie verschiedene Bilder. Wirklich sieht der 1. Beobachter folgende Anordnung vom Mittelpunkt: 3, 2, 1, während der 2. Beobachter andere Reihenfolge sieht: 1, 3, 2, und nur der 3. Beobachter wird das ursprüngliche Bild sehen: 1, 2, 3. Wir haben da einen Widerspruch. Nehmen wir jetzt an, dass sich die Geometrie der rotierenden Ebene geändert hat. Was wird dann mehr bevorzugt: oben oder unten? Die Aufgabe ist doch symmetrisch. Wohin hat sich die Ebene gekrümmt? Wenn wir die letzte Annahme machen, dass sich der Radius gekrümmt hat (wie sich die sichtbare Bewegung im Nichtinertialsystem ändert), so sieht der 2. Beobachter ihn nicht gekrümmt, und der 1. und der 3. werden ihn für "gekrümmt" in verschiedene Seiten halten. Auf solche Weise sehen drei Beobachter im einem und demselben Punkt eines und desselben Raumes verschiedene Bilder. Folglich ist die Krümmung nicht objektiv (kann kein Objekt der wissenschaftlichen Forschung sein).

Der rotierende Kreis beweist die Widersprüchlichkeit der Ideen der SRT sowie der ART. Wirklich ändert sich der zur Bewegung senkrechte Radius laut Lehrbüchern nicht. Also bleiben die Kreise an ihren Stellen unabhängig von der Bewegung. Setzen wir die Beobachter auf dem ruhenden Kreis äquidistant und lösen einen Punktausbruch aus dem Mittelpunkt des Kreises aus, damit die Beobachter die Striche auf dem bewegten Kreis zum Zeitpunkt der Ankunft des Signals (Abb. 2.2) aufgetragen haben.

Abbildung 2.2: Äquidistante Beobachter auf dem Kreis.

Infolge der Symmetrie der Aufgabe werden die Striche auch äquidistant. Bei den nachfolgenden periodischen Ausbrüchen wird jeder Beobachter bestätigen, dass das Strichzeichen (bei entsprechender Periodizität der Ausbrüche) zum Zeitpunkt des Ausbruchs an ihm vorbei geht, das heißt, die Längen der Abschnitte der ruhenden und rotierenden Kreise sind gleich. Bei dem Stillstand des Kreises bleiben die Zeichen an ihrer Stelle. Die Zahl von äquidistanten Zeichen (gleich der Anzahl der Beobachter) wird sich nicht ändern. Also sind die Längen der Abschnitte im ruhigen Fall auch gleich. So war gar keine Längenverkürzung (und Veränderungen der Geometrie).

Betrachten wir wieder eine Frage über die Geometrie des Raumes, aber andererseits. Diese Frage ist noch von der Gauß-Zeit ganz verwickelt, der die Geometrie mit Hilfe von Lichtstrahlen bestimmen wollte. Die Beschränktheit dieser oder jener Versuche kann doch die idealen mathematischen Begriffe nicht beeinflussen. Es sei bemerkt, dass sich das Licht in der ART sogar nicht nach der kürzesten Linie bewegt: anstelle des Ferma-Prinzips $\delta\int dl=0$ haben wir in der ART [17]: $\delta\int {(1/\sqrt{g_{00}})dl} = 0$, wo $g_{\alpha\beta}$ der metrische Tensor ist. Wodurch ist doch das Licht in diesem Fall abgesondert? Häufig wird die Notwendigkeit der Veränderung der Geometrie in Lehrbüchern auf folgende Weise "begründet": damit das Licht das geschlossene Dreieck im Gravitationsfeld aufzeichnet, sollen die Spiegel auf einen bestimmten Winkel umgedreht sein, daraufhin wird sich die Summe der Winkel des Dreieckes von $\pi$ unterscheiden. Jedoch kann man für jeden Punktkörper und 3 Reflektoren im Schwerefeld (s. Abb. 2.3) die Summe der "Winkel" aufzeichnen:

$$\sum\beta_i = \pi + 4\arctan{\Biggl ( {gL\over 2v_0^2}\Biggr ) } - 2\arctan{\Biggl ( {gL\over v_0^2}\Biggr ) }.$$

Abbildung 2.3: "Geometrie des Dreiecks".

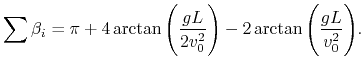
Es ergibt sich, dass die Geometrie eines und desselben Raumes von den Bedingungen des Versuches abhängt: von $L$ und $v_0$. Da man den Winkel $\alpha$ zwischen den Spiegeln $A$ und $B$ auch tauschen kann (auf unserer Abbildung ist er als Null $\alpha=0$), bekommen wir die Möglichkeit der künstlichen Veränderung der Geometrie im großen Ausmaß. Es sei bemerkt, dass die variablen Parameter $\alpha$ und $L$ auch für das Licht gültig bleiben. In ähnlichen "glaubwürdigen" Beweisen über die Notwendigkeit der Veränderung der Geometrie werden einige Momente nicht betont. Erstens wird die Geometrie sowie im Versuch mit den Massenpunkten, als auch mit dem Licht nicht im Nu "aufgezeichnet", sondern konsequent im Laufe bestimmter Zeit. Zweitens bewegen sich die Teilchen (und das Licht) für beschleunigte Systeme im Vakuum geradlinig nach dem Trägheitsgesetz, und tatsächlich legt sich auf diese Bewegung die Bewegung der Grenzen dieses beschleunigten Systems additiv. Alle Einfallswinkel (im Laborsystem) sind den entsprechenden Reflexionswinkeln gleich, und "die Geometrie der Winkel" ändert sich gar nicht. Einfach ergibt sich die Figur infolge der Bewegung der Grenzen als ungeschlossen. Drittens wird die Rolle der Grenzen bei der Bestimmung der Verhältnisse zwischen den Längen der realen Körper gar nicht aufgedeckt. Zum Beispiel, wenn alle Punkte des realen Körpers der Wirkung der identischen beschleunigenden Kraft unterworfen sind, so bleibt das gegenseitige Verhältnis der Längen und der Winkel ("Geometrie") unveränderlich. Wenn nur die Grenzen der Beschleunigung unterworfen sind, so gehen alle realen Veränderungen der Größen der Körper nur in der Wechselwirkung mit den Grenzen. Auf jeden Fall kann man die Geraden von Euklid ziehen. Zum Beispiel, nehmen wir für die Durchführung der horizontalen Geraden im Gravitationsfeld zwei identische lange Kerne (Abb. 2.4).

Abbildung 2.4: Ziehen der Geraden im Schwerefeld.

Die Punktstütze für den ersten Kern stellen wir in der Mitte des Kernes auf. Infolge der Krümmung des Kernes bildet sich eine konvexe Linie. Zwei Punktstützen für den zweiten Kern stellen wir in der Höhe von zwei herabfallenden Enden des ersten Kernes auf. Infolge der Krümmung des zweiten Kernes bildet sich eine konkave Linie. Die mittlere Linie zwischen diesen zwei gekrümmten Kernen bestimmt die Gerade.