Nächste: Zusätzliche Kritik Nach oben: Kinematik der speziellen Relativitätstheorie Vorhergehende: Einige Bemerkungen Inhaltsverzeichnis
Wir möchten Sie daran erinnern, dass sich die Kinematik mit der Suche nach den Gründen der Bewegung nicht beschäftigt, sondern behauptet, zum Beispiel, folgendes: wenn die Geschwindigkeiten vorgegeben sind, kann man das Ergebnis der Geschwindigkeitsaddition finden. Die Fragen der Dynamik der Teilchen (die befasst sich mit den Gründen der Bewegungen) fordern eine abgesonderte Betrachtung (s. Kapitel 4).
Machen wir jetzt eine Bemerkung über die relativistischen Gesetze der
Geschwindigkeitsaddition. Für zwei Systeme, die unmittelbar an der relativen
Bewegung teilnehmen, entsteht kein Zweifel bei der Bestimmung ihrer relativen
Geschwindigkeit (weder in der klassischen Physik, noch in der SRT). Das System
![]() soll sich bezüglich des Systems
soll sich bezüglich des Systems ![]() mit der Geschwindigkeit
mit der Geschwindigkeit ![]() bewegen;
es ist ähnlich, das System
bewegen;
es ist ähnlich, das System ![]() bewegt sich bezüglich
des Systems
bewegt sich bezüglich
des Systems ![]() mit der Geschwindigkeit
mit der Geschwindigkeit ![]() . Tatsächlich bestimmt das relativistische Gesetz der
Geschwindigkeitsaddition die relative Geschwindigkeit jener Bewegung, an der der
Beobachter selbst nicht teilnimmt. Die Geschwindigkeit der Bewegung des Systems
. Tatsächlich bestimmt das relativistische Gesetz der
Geschwindigkeitsaddition die relative Geschwindigkeit jener Bewegung, an der der
Beobachter selbst nicht teilnimmt. Die Geschwindigkeit der Bewegung des Systems
![]() bezüglich des Systems
bezüglich des Systems ![]() wird sich so bestimmen:
wird sich so bestimmen:
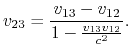 |
(1.5) |
Gerade in solcher Form (obwohl wird ![]() durch
durch
![]() und
und ![]() gewöhnlich ausgedrückt) wird das wahrhafte Wesen dieses Gesetzes geöffnet: er
besagt, welche relative Geschwindigkeit der Systeme
gewöhnlich ausgedrückt) wird das wahrhafte Wesen dieses Gesetzes geöffnet: er
besagt, welche relative Geschwindigkeit der Systeme ![]() und
und ![]() der Beobachter in
der Beobachter in ![]() registrieren wird, wenn er die Einsteinregel für die Zeitsynchronisation (mit
Hilfe der Lichtsignale) und die Längenmessung benutzen wird. In der Tat haben
wir "das Scheingesetz" wieder. (Für den Fall der möglichen parametrischen
Abhängigkeit der Lichtgeschwindigkeit von der Frequenz wird der Ausdruck
geändert – s. Anlagen.)
registrieren wird, wenn er die Einsteinregel für die Zeitsynchronisation (mit
Hilfe der Lichtsignale) und die Längenmessung benutzen wird. In der Tat haben
wir "das Scheingesetz" wieder. (Für den Fall der möglichen parametrischen
Abhängigkeit der Lichtgeschwindigkeit von der Frequenz wird der Ausdruck
geändert – s. Anlagen.)
Betrachten wir folgende methodische Bemerkung. Recht seltsam für kinematische Begriffe ist die Nichkommutativität des relativistischen Gesetzes der Geschwindigkeitsaddition für nichtkollineare Vektoren. Die Eigenschaft der Nichkommutativität (und daß die Lorentztransformationen ohne Drehungen keine Gruppe bilden) wird kaum in einigen Lehrbüchern für theoretische Physik erwähnt. Doch ändert ähnliche Eigenschaft, zum Beispiel, in der Quantenmechanik den ganzen mathematischen Apparat wesentlich und drückt physisch die gleichzeitige Nichtmessbarkeit der nicht kommutierenden Größen aus.
Aus dem allgemeinen relativistischen Gesetz der Geschwindigkeitsaddition
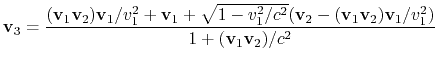 |
(1.6) |
werden wir die Nichtnullgeschwindigkeit bekommen, die von den
Geschwindigkeiten ![]() und
und ![]() recht
kompliziert abhängt.
recht
kompliziert abhängt.
Die konsequente Anwendung der Transformationen (Bewegungen) ![]() und
und ![]() bringt zu
bringt zu
und in der anderen Ordnung ![]() und
und ![]() bringt zu
bringt zu
das heißt, wir bekommen verschiedene Vektoren (Abb. 1.21).
Was kann die Zerlegung des Vektors der Geschwindigkeit in die Komponenten in diesem Fall bedeuten? Erstens ist die Versetzung der klassischen Elementarmethoden der Berechnungen (die kommutative Algebra) auf die relativistischen Gleichungen (nichtkommutative) unrechtmäßig: sogar die Lösung der vektoriellen Gleichungen komponentenmäßig erfordert zusätzliche Postulate, Komplizierungen oder Erläuterungen. Zweitens ist die einfache Anwendung der Methoden der klassischen Physik (des Prinzips der virtuellen Versetzungen, der Variationsmethoden usw.) unmöglich. Man sollte sogar die Null "individualisieren": die Zahl "der Nullgrößen", die aus bestimmter vektorieller Kombination zusammengesetzt sind, soll der Zahl "der Nullgrößen" gleich sein, die aus der vektoriellen Spiegelkombination gebildet sind. Also würde die Theorie der Fluktuationen auch eine zusätzliche Begründung brauchen. So sollte man trotz der These "über die Einfachheit und die Eleganz der SRT" für die richtige Begründung sogar der Elementarprozeduren eine Menge von künstlichen Komplizierungen und Erläuterungen einführen (was in Lehrbüchern fehlt).
Betrachten wir einen logischen Widerspruch des relativistischen Gesetzes der Geschwindigkeitsaddition am Beispiel des eindimensionalen Falls. Mögen wir die Waage haben, die die Form der waagerechten Rinne mit der waagerechten querlaufenden Achse in der Mitte der Rinne hat. In der Rinne werden zwei gleiche Kugeln der Masse m in verschiedenen Richtungen von der Achse (Abb. 1.22) rollen.
Um jetzt den Besprechungen der Eigenschaften der relativistischen Masse zu entgehen, werden wir folgenderweise handeln. Es fehle die Reibung der Waageachse überall, ausschließlich den Punkt der waagerechten Lage ("der tote Punkt"). In dieser Lage lässt die Schwelle der Reibungsrkaft der Waage nicht zu, sich durch mögliche kleine Differenzen der relativistischen Massen in Bewegung zu setzen (zwischen den Kugeln), aber diese Schwelle der Sensibilität kann das Drehen der Waage (vom "toten Punkt") beim Fehlen einer der Kugeln nicht verhindern (falls die fällt).
Mögen die Geschwindigkeiten der Kugeln im System der Waage dem Modul nach
identisch sein. Dann rollen die Kugeln in diesem System gleichzeitig bis zu den
Rändern und fallen nach unten so, dass die Waage in der waagerechten Lage
bleibt. Betrachten wir jetzt dieselbe Bewegung im System, bezüglich dessen sich
die Waage mit der Geschwindigkeit ![]() bewegt. Es soll nur
bewegt. Es soll nur ![]() , und
, und ![]() , wo
, wo ![]() die Schallgeschwindigkeit im Rinnenmaterial ist. Dann kann man
die Waage für absolut unnachgiebig halten (Schallwellen ignorieren). Laut dem
relativistischen Gesetz der Geschwindigkeitsaddition
die Schallgeschwindigkeit im Rinnenmaterial ist. Dann kann man
die Waage für absolut unnachgiebig halten (Schallwellen ignorieren). Laut dem
relativistischen Gesetz der Geschwindigkeitsaddition
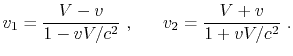
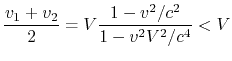
Ob die Lorentztransformationen die konsequenten Übergänge von einem Inertialsystem zum anderen beschreiben können und ob das relativistische Gesetz der Geschwindigkeitsaddition den realen Geschwindigkeitsveränderungen entspricht? Natürlich, nicht. Fürs erste werden wir Sie daran erinnern, welcher Sinn ins relativistische Gesetz der Geschwindigkeitsaddition eingelegt wurde. Es soll beweisen, dass die Addition der Bewegungen zur Geschwindigkeit nicht bringen kann, die höher als die Lichtgeschwindigkeit ist. Wie kann man die Bewegungen in diesem Fall addieren? Zum Beispiel bewegt sich unsere Erde (tatsächlich existiert das erste bewegte Bezugssystem) bezüglich der Sterne, von der Erde startet das Raumschiff mit großer Geschwindigkeit (tatsächlich ist das zweite bewegte Bezugssystem "geschaffen"), dann von diesem Raumschiff startet die nächste Rakete (das dritte Bezugssystem) usw. Gerade es soll unter der konsequenten Anwendung der Transformationen gemeint werden. Dann fällt, zum Beispiel, die Frage darüber weg, welche Geschwindigkeit man im Gesetz der Geschwindigkeitsaddition für die erste und welche für die zweite halten soll (es ist für nichtkommutative Transformationen wichtig). In diesem Sinne wurden alle Beispiele oben angeführt.
Betrachten wir jetzt die Lorentztransformationen für willkürliche Richtungen der Bewegung:
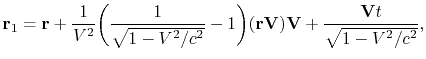
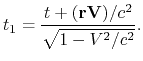
| (1.7) |
Wir werden zu einem willkürlichen Vektor ![]() konsequent die Lorentztransformationen mit demselben Satz der
Geschwindigkeiten verwenden. Wir haben:
konsequent die Lorentztransformationen mit demselben Satz der
Geschwindigkeiten verwenden. Wir haben:
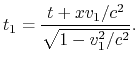
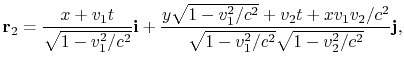
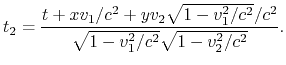
Wir werden die Ausdrücke für ![]() und
und
![]() in der offenbaren Art wegen ihrer Sperrigkeit
nicht ausschreiben.
in der offenbaren Art wegen ihrer Sperrigkeit
nicht ausschreiben.
Die graphischen Programme verwendend, kann man sich jedoch folgender
Eigenschaften vergewissern:
1) die Anfangszeit ist im neuen System in einem
beliebigen Punkt des Raumes, außer dem Anfang der Koordinaten entsynchronisiert.
2) die Zeiträume haben sich geändert: ![]() , das heißt, wir sind nicht ins ursprüngliche
ruhende System sondern in ein neues bewegtes System geraten. Also wird der Sinn
der Lorentztransformationen oder des relativistischen Gesetzes der
Geschwindigkeitsaddition mindestens in Lehrbüchern nicht ganz genau erschlossen.
, das heißt, wir sind nicht ins ursprüngliche
ruhende System sondern in ein neues bewegtes System geraten. Also wird der Sinn
der Lorentztransformationen oder des relativistischen Gesetzes der
Geschwindigkeitsaddition mindestens in Lehrbüchern nicht ganz genau erschlossen.
3) Die Abschnitte zeigen sich nicht nur mit geänderter Länge sondern auch
umgedreht. Davon kann man sich leicht überzeugen, wenn man den Winkel der
Wendung numerisch findet, das heißt die Differenz
![$\displaystyle \alpha = \arctan\Biggl ( {y_3[x(1),y(1),t]-y_3[x(0),y(0),t]\over
x_3[x(1),y(1),t]-x_3[x(0),y(0),t]}\Biggr ) -
$](img184.png)
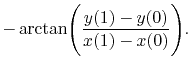
Versuchen wir zu klären, warum die Deutungen aus Lehrbüchern zur
Nichtübereinstimmung zweier Ausdrücke bringen: des relativistischen Gesetzes
Geschwindigkeitsaddition und der Lorentztransformationen, obwohl der erste
Ausdruck aus dem zweiten abgeleitet wird. Wir erinnern Sie an diese
Schlussfolgerung am Beispiel der eindimensionalen gegenseitigen Bewegung der
Systeme ![]() und K'. Ausgehend von den
Lorentztransformationen
und K'. Ausgehend von den
Lorentztransformationen
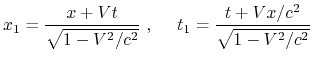
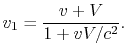
Dem Wesen der Formel nach können wir zur zweiten Substitution für die
Definition ![]() einfach nicht übergehen, obwohl es
formell möglich ist, konsequent in den Ausdruck des relativistischen Gesetzes
der Geschwindigkeitsaddition soviel man will Geschwindigkeitsgrößen zu
substituieren. Im Falle der Addition der Bewegungen entlang einer Geraden bleibt
die klassische Eigenschaft der Kommutativität erhalten, und der Widerspruch ist
verschleiert. Aber falls die Geschwindigkeitsvektoren nichtkollinear sind, so
zeigt sich der Punkt 3) als falsch, und sofort kommen die Widersprüchlichkeit
und die Nichtübereinstimmung des Gesetzes der Geschwindigkeitsaddition und der
Lorentztransformationen zum Ausdruck.
einfach nicht übergehen, obwohl es
formell möglich ist, konsequent in den Ausdruck des relativistischen Gesetzes
der Geschwindigkeitsaddition soviel man will Geschwindigkeitsgrößen zu
substituieren. Im Falle der Addition der Bewegungen entlang einer Geraden bleibt
die klassische Eigenschaft der Kommutativität erhalten, und der Widerspruch ist
verschleiert. Aber falls die Geschwindigkeitsvektoren nichtkollinear sind, so
zeigt sich der Punkt 3) als falsch, und sofort kommen die Widersprüchlichkeit
und die Nichtübereinstimmung des Gesetzes der Geschwindigkeitsaddition und der
Lorentztransformationen zum Ausdruck.
Im früher betrachteten Beispiel kann man anders handeln: wir werden die Reihenfolge von drei Transformationen der Geschwindigkeiten suchen, die die ursprüngliche Zeit in den Lorentztransformationen unveränderlich beibehält. Dann ist es leicht zu überprüfen, dass die einzige Reihenfolge anstelle (1.7) genommen werden kann:
| (1.8) |
Doch bleibt erstens die Wendung der Abschnitte. Zweitens befriedigt der neue
Satz der Geschwindigkeiten in der gegebenen Reihenfolge das Gesetz der
Geschwindigkeitsaddition nicht, das heißt, es hat sich die Ordnung der
Substitution der Geschwindigkeiten ![]() und
und ![]() ins Gesetz der Geschwindigkeitsaddition tatsächlich geändert (was dem Wesen
dieses Gesetzes nicht entspricht). Auf solche Weise werden die Widersprüche
einerlei nicht beseitigt. Eine der Erscheinungsformen der Widersprüchlichkeit
der SRT ist die Thomas-Präzession: ausgehend von der Reihenfolge der
Inertialsysteme (die sich geradlinig und gleichmäßig bewegen), erhält man
plötzlich im Ergebnis das Drehen des Gegenstandes (grundsätzlich keine
Inertialbewegung). So enthält der Übergang von den in den standardmäßigen
Lehrbüchern dargelegten Lorentztransformationen im "mathematischen Raum" 1+1
(
ins Gesetz der Geschwindigkeitsaddition tatsächlich geändert (was dem Wesen
dieses Gesetzes nicht entspricht). Auf solche Weise werden die Widersprüche
einerlei nicht beseitigt. Eine der Erscheinungsformen der Widersprüchlichkeit
der SRT ist die Thomas-Präzession: ausgehend von der Reihenfolge der
Inertialsysteme (die sich geradlinig und gleichmäßig bewegen), erhält man
plötzlich im Ergebnis das Drehen des Gegenstandes (grundsätzlich keine
Inertialbewegung). So enthält der Übergang von den in den standardmäßigen
Lehrbüchern dargelegten Lorentztransformationen im "mathematischen Raum" 1+1
(![]() ) zu den Lorentztransformationen im "Raum" 1+2 oder
1+3 physische Widersprüche.
) zu den Lorentztransformationen im "Raum" 1+2 oder
1+3 physische Widersprüche.
Viele intuitiv verständliche Eigenschaften von physischen Größen verlieren in der SRT ihren Sinn. Zum Beispiel, die relative Geschwindigkeit hört auf, invariant zu sein. Die Teilchen, die entlang einer Geraden mit verschiedenen Geschwindigkeiten rausfliegen, bilden in der SRT einen komplizierten "Fächer der Geschwindigkeiten" für das bewegte System. Die isotrope Verteilung nach den Geschwindigkeiten in der SRT hört auf, als solche für ein anderes bewegtes System zu sein. In Wirklichkeit gibt es in der SRT keine deklarierte Vereinfachung.
Aus der SRT folgt die Unmöglichkeit der Geschwindigkeiten ![]() ganz und gar nicht. Und die Ergänzung dazu, dass es sich nur
auf die Geschwindigkeit der Signalübertragung bezieht, ist eine künstliche
Ergänzung (wegen des Vorhandenseins der offensichtlichen Gegenbeispiele zur
erweiterten Erläuterung). Jedoch bleibt der Begriff des Signals (der
Information) sogar mit ähnlicher Ergänzung ungenügend determiniert. Zum Beispiel
sind wir nicht sicher, wenn wir das Signal vom superneuen Aufblitzen bekommen,
daß solche Information in der diametral entgegengesetzten Entfernung vom
superneuen Aufblitzen "enthalten ist", das heißt, wir wissen davon mit der
Geschwindigkeit
ganz und gar nicht. Und die Ergänzung dazu, dass es sich nur
auf die Geschwindigkeit der Signalübertragung bezieht, ist eine künstliche
Ergänzung (wegen des Vorhandenseins der offensichtlichen Gegenbeispiele zur
erweiterten Erläuterung). Jedoch bleibt der Begriff des Signals (der
Information) sogar mit ähnlicher Ergänzung ungenügend determiniert. Zum Beispiel
sind wir nicht sicher, wenn wir das Signal vom superneuen Aufblitzen bekommen,
daß solche Information in der diametral entgegengesetzten Entfernung vom
superneuen Aufblitzen "enthalten ist", das heißt, wir wissen davon mit der
Geschwindigkeit ![]() ? Oder ist es keine Information? Also kann
nur die Information auf dem materiellen Träger elektromagnetischer Natur in der
SRT in Absicht sein, die sich im Vakuum konsequent durch alle Punkte des Raumes
von der Quelle bis zum Signalempfänger verbreitet.
? Oder ist es keine Information? Also kann
nur die Information auf dem materiellen Träger elektromagnetischer Natur in der
SRT in Absicht sein, die sich im Vakuum konsequent durch alle Punkte des Raumes
von der Quelle bis zum Signalempfänger verbreitet.
Machen wir noch eine Bemerkung über die "Merkwürdigkeit" des relativistischen
Gesetzes Geschwindigkeitsaddition, die zulässt, Lichtsignale sogar dann
auszutauschen, wenn sich die algebraische Summe der Geschwindigkeiten größer
zeigt. Lenken wir die Aufmerksamkeit auf die offensichtliche Tatsache: die
Signale für den Austausch von Information sollen unbedingt in der Richtung des
Objektes und nicht in der entgegengesetzten Richtung geschickt werden. Deshalb
gibt es nichts Merkwürdiges im Austausch der Signale, wenn sich ![]() im klassischen Fall infolge der formalen Addition der
Geschwindigkeiten erweist. Es sollen zwei Flugzeuge vom Flugplatz
im klassischen Fall infolge der formalen Addition der
Geschwindigkeiten erweist. Es sollen zwei Flugzeuge vom Flugplatz ![]() mit den Geschwindigkeiten
mit den Geschwindigkeiten ![]() auffliegen und fliegen in entgegengesetzten
Richtungen der Achse
auffliegen und fliegen in entgegengesetzten
Richtungen der Achse ![]() (das heißt, mit der relativen
Geschwindigkeit
(das heißt, mit der relativen
Geschwindigkeit ![]() )
auseinander. Ob der Austausch von Schallsignalen zwischen ihnen möglich ist?
Natürlich! Da sich die Schallwelle in der Luft unabhängig von der
Geschwindigkeit der Quelle
)
auseinander. Ob der Austausch von Schallsignalen zwischen ihnen möglich ist?
Natürlich! Da sich die Schallwelle in der Luft unabhängig von der
Geschwindigkeit der Quelle ![]() im Zeitpunkt der
Aussendung des Signals fortpflanzt, so wird das erste Flugzeug (das Signal
gesendete) die Wellenfront einholen, die sich in der positiven Richtung der
Achse
im Zeitpunkt der
Aussendung des Signals fortpflanzt, so wird das erste Flugzeug (das Signal
gesendete) die Wellenfront einholen, die sich in der positiven Richtung der
Achse ![]() erstreckt, und das zweite Flugzeug wird mit der
Wellenfront "wetteifern", die sich in der negativen Richtung der Achse
erstreckt, und das zweite Flugzeug wird mit der
Wellenfront "wetteifern", die sich in der negativen Richtung der Achse ![]() erstreckt. Beide Flugzeuge bewegen sich langsamer, als sich die
nächsten von ihnen entsprechenden Abschnitte der Wellenfront fortpflanzen
(Abb. 1.23).
erstreckt. Beide Flugzeuge bewegen sich langsamer, als sich die
nächsten von ihnen entsprechenden Abschnitte der Wellenfront fortpflanzen
(Abb. 1.23).
Es liegt offen zutage, dass die physische Beschränkung der Geschwindigkeitsgröße von der Mathematik nicht aufgelegt werden kann (die Tatsache, dass negative Größe in einigen Ausdrücken unter dem Wurzelzeichen stehen wird). Man soll sich einfach daran erinnern, dass alle SRT-Formeln unter Anwendung des Austausches von Lichtsignalen (Einstein-Methode der Synchronisation) abgeleitet sind. Wenn sich der Körper sofort schneller als das Licht bewegt, so kann ihn das Signal einfach nicht einholen, das hinterher geschickt ist. Analog ist es möglich, die Synchronisation mit Hilfe des Schalls einzuführen und (es werden auch Besonderheiten in den Formeln vorkommen), aber daraus wird die Unmöglichkeit der Überschallgeschwindigkeiten ganz und gar nicht folgern. Die Geschwindigkeit der Verbreitung von Erregungen (Schall-oder Lichterregungen) im Medium ist keinesfalls mit der Geschwindigkeit der Bewegung eines Körpers durch dieses Medium verbunden.
Artecha S.N.