Nächste: Lorentztransformationen Nach oben: Kinematik der speziellen Relativitätstheorie Vorhergehende: Zusätzliche Bemerkungen Inhaltsverzeichnis
Nach der Kritik des Basisbegriffes Zeit setzen wir die Analyse der logischen
Grundlagen dieser Theorie fort und betrachten den Hilfsbegriff
"Gleichzeitigkeitsrelativität". Wir machen Sie an das Gedankenexperiment aus
der SRT erinnerlich. Es fahre der Zug A'B' mit der Geschwindigkeit ![]() auf der Eisenbahn. In den Bahnkörper (
auf der Eisenbahn. In den Bahnkörper (![]() )
gegenüber der Mitte des Zuges C' (zum Zeitpunkt des Zusammenfallens der
Punkte C=C') schlägt der Blitz ein. Im System, das mit dem sich
bewegenden Zug verbunden ist, erreicht dann der Lichtblitz gleichzeitig die
Punkte A' und B', während der Lichtblitz aus Sicht des ruhenden
Beobachters gleichzeitig die Punkte
)
gegenüber der Mitte des Zuges C' (zum Zeitpunkt des Zusammenfallens der
Punkte C=C') schlägt der Blitz ein. Im System, das mit dem sich
bewegenden Zug verbunden ist, erreicht dann der Lichtblitz gleichzeitig die
Punkte A' und B', während der Lichtblitz aus Sicht des ruhenden
Beobachters gleichzeitig die Punkte ![]() und
und ![]() (mit
der Mitte im Punkt
(mit
der Mitte im Punkt ![]() ) erreicht, aber zu diesem Zeitpunkt gehen
die Punkte
) erreicht, aber zu diesem Zeitpunkt gehen
die Punkte ![]() und C' (die Mitten der Abschnitte) mit
einiger Entfernung auseinander. Doch ist ähnliche Situation in der klassischen
Physik möglich, wenn wir die Information von den Punkten
und C' (die Mitten der Abschnitte) mit
einiger Entfernung auseinander. Doch ist ähnliche Situation in der klassischen
Physik möglich, wenn wir die Information von den Punkten ![]() in
den neuen einheitlichen Punkt
in
den neuen einheitlichen Punkt ![]() (oder im Gegenteil aus
dem Punkt
(oder im Gegenteil aus
dem Punkt ![]() in die Punkte
in die Punkte ![]() ) mit einer Endgeschwindigkeit
) mit einer Endgeschwindigkeit ![]() überzugeben wollen (dabei werden die SRT und die Beständigkeit
der Lichtgeschwindigkeit keine Rolle spielen).
überzugeben wollen (dabei werden die SRT und die Beständigkeit
der Lichtgeschwindigkeit keine Rolle spielen).
Man kann folgendes mechanisches Modell (Abb. 1.11) anbieten.
Es sollen auch 4 Massenpunkte (ohne Schwerekraft) mit der Geschwindigkeit
Man kann sagen, dass es zwei verschiedene Ereignisse sind. Es sind im Fall
mit dem Aufblitzen (dem Blitz) auch zwei. In Tat soll es zum Zeitpunkt des
Zusammenfallens der Mittelpunkte Analysieren wir jetzt ausführlicher das Gedankenexperiment, das die
Gleichzeitigkeitsrelativität "demonstriert": soll das Aufblitzen zum Zeitpunkt
des Zusammenfallens der Mittelpunkte Denken wir daran zurück, dass die positive Hauptidee der SRT in der
Zeitlichkeit der Übertragungsgeschwindigkeit von Wechselwirkungen bestand.
Dieselbe Idee äußert die Theorie der kurzreichweitigen Wechselwirkung und
spiegelt das Feldherangehen (durch die Maxwell-Gleichungen) wider: die
Lichtfront von der Quelle bis zum Empfänger geht konsequent alle Zwischenpunkte
des Raumes durch. Eben mit dieser Eigenschaft kommt der Begriff der
Gleichzeitigkeitsrelativität in Widerspruch (Abb. 1.12).
Für den Beweis wenden wir zwei Behauptungen von der SRT an: 1)ein und
dasselbe Aufblitzen erreicht die Beobachter, die sich bezüglich einander
bewegen, gleichzeitig, obwohl sich die Beobachter während des Durchganges des
Lichtes räumlich voneinander mit einiger Entfernung trennen; 2) die
kinematischen Formeln der SRT (aus Lehrbüchern) enthalten nur das Quadrat der
Geschwindigkeit. Der erste Beobachter soll, zum Beispiel, im System S' in
der Richtung der Quelle des Aufblitzens mit der kleinen Geschwindigkeit Einerseits, da die Formeln der SRT nur das Quadrat der Geschwindigkeit
enthalten, wird der zweite Beobachter die Zeit des Signalempfanges vom ersten
und dritten Beobachter für identisch halten. Man kann sich über die Aussendung
zusätzlicher eigener Signale ohne Verzögerung beim Erhalten von jedem Beobachter
des untersuchten Signals vereinbaren. Falls die Berechnungen des zweiten
Beobachters richtig sind, soll er die Signale vom ersten und dritten Beobachter
gleichzeitig erhalten (die Aufgabe ist symmetrisch). Andererseits pflanzt sich
das Licht laut den Maxwell-Gleichungen ununterbrochen fort, und der zweite
Beobachter erhält das Signal vom ersten gleichzeitig damit, wenn er selbst das
erforschende Signal sieht. Aus Sicht des zweiten Beobachters ist das Licht beim
dritten Beobachter zu dieser Zeit noch nicht angekommen. So kommt der zweite
Beobachter in Widerspruch mit sich: die ersten Berechnungen nach den Formeln der
SRT widersprechen den zweiten Berechnungen nach den Maxwell-Gleichungen. Es ist
ersichtlich, dass die Beobachter das Aufblitzen nicht gleichzeitig sehen werden,
sondern nacheinander, da der Raumweg des Lichtes einheitlich ist: die Quelle,
der erste Beobachter, dann der zweite und schließlich der dritte Beobachter.
Zusätzlich sei bemerkt, dass der Begriff Gleichzeitigkeitsrelativität sogar
in den Rahmen der SRT stark beschränkt ist: er ist nur auf zwei isolierte
Ereignisse anzuwenden (es gibt keine kreuzenden Grundursachen, keine kreuzenden
Nachhandlungen, und überhaupt interessieren uns keine zusätzlichen Tatsachen).
Tatsächlich haben die Lichtkegel für diese gewählten Punkte Kreuzungen, zu
geschweigen aller anderen Punkte in Raum und Zeit. In Wirklichkeit haben wir die
ununterbrochenen Ketten kausal gebundener(und nicht gebundener) Ereignisse, die
mit einer Mehrzahl der Kreuzungen durch jeden Punkt des Raumes und der Zeit
gehen (bei weitem ruft nicht jeder Grund den Eintritt der entsprechenden Folge
mit Lichtgeschwindigkeit hervor). Und das ganze reale (von verschiedenen
Maßstäben!) Zeitnetz hat die Wechselwirkung für den ganzen Raum. Also können wir
im allgemeinen Fall die Reihenfolge sogar kausal ungebundener Ereignisse
(irgendwo sollte es einerlei widergespiegelt werden) nicht tauschen (durch die
Auswahl des Bezugssystems).
![]() paarweise über dem Punkt
paarweise über dem Punkt ![]() (neben dem Bahnkörper) und über der Mitte des Zuges C' (die stimmt mit dem Punkt
(neben dem Bahnkörper) und über der Mitte des Zuges C' (die stimmt mit dem Punkt ![]() zum Zeitpunkt des Fallen überein, neben dem Punkt
zum Zeitpunkt des Fallen überein, neben dem Punkt ![]() ) fallen. Es sollen
ideale Reflektoren im Punkt
) fallen. Es sollen
ideale Reflektoren im Punkt ![]() und in der Mitte des
Zuges (gleichschenklige Dreiecke mit dem Basiswinkel
und in der Mitte des
Zuges (gleichschenklige Dreiecke mit dem Basiswinkel ![]() )
aufgestellt werden. Dann fliegen zwei Teilchen, die sich über dem Bahnkörper
widerspiegelten (im Punkt
)
aufgestellt werden. Dann fliegen zwei Teilchen, die sich über dem Bahnkörper
widerspiegelten (im Punkt ![]() ), in verschiedenen
Richtungen mit der Geschwindigkeit
), in verschiedenen
Richtungen mit der Geschwindigkeit ![]() und erreichen
gleichzeitig die Punkte
und erreichen
gleichzeitig die Punkte ![]() und
und ![]() (in
der Klassik
(in
der Klassik ![]() ). Dazu braucht man die Zeit
). Dazu braucht man die Zeit ![]() , wo
, wo
![]() - die Länge des Zuges ist. Zwei andere Teilchen,
die sich über der Mitte des Zuges C' widerspiegelten, werden sich
bezüglich der Eisenbahn mit den Geschwindigkeiten
- die Länge des Zuges ist. Zwei andere Teilchen,
die sich über der Mitte des Zuges C' widerspiegelten, werden sich
bezüglich der Eisenbahn mit den Geschwindigkeiten ![]() vorwärts und
vorwärts und ![]() rückwärts bewegen. In derselben Zeit
rückwärts bewegen. In derselben Zeit ![]() legt
das erste dieser Teilchen die Strecke (vorwärts)
legt
das erste dieser Teilchen die Strecke (vorwärts)
![]() zurück, und da der Zug die Strecke
zurück, und da der Zug die Strecke ![]() bewältigt, erreicht das
Teilchen den Punkt A'. Analog für das zweite Teilchen
bewältigt, erreicht das
Teilchen den Punkt A'. Analog für das zweite Teilchen ![]() ;
folglich erreicht es den Punkt B'. Auf solche Weise wird das Ereignis -
das Fallen der Punkte auf die Reflektoren - in allen vier Punkten gleichzeitig
fixiert: sowie in den Punkten
;
folglich erreicht es den Punkt B'. Auf solche Weise wird das Ereignis -
das Fallen der Punkte auf die Reflektoren - in allen vier Punkten gleichzeitig
fixiert: sowie in den Punkten ![]() und
und ![]() (über
der Eisenbahn), als auch in den Punkten A' und B' (über dem Zug).
Es war der Fall, wo die Massenteilchen, die über dem Zug fielen,
nahmen auch an seiner Trägheitsbewegung teil. Sollte das zweite
Massenteilchenpaar (über den Bahnschienen) auf einen unbeweglichen
Punkt
(über
der Eisenbahn), als auch in den Punkten A' und B' (über dem Zug).
Es war der Fall, wo die Massenteilchen, die über dem Zug fielen,
nahmen auch an seiner Trägheitsbewegung teil. Sollte das zweite
Massenteilchenpaar (über den Bahnschienen) auf einen unbeweglichen
Punkt ![]() fallen, dann müsste der Dreiecksreflektor am Zug folgende
Basiswinkel haben:
fallen, dann müsste der Dreiecksreflektor am Zug folgende
Basiswinkel haben: ![]() - entgegen der Zugbewegung und
- entgegen der Zugbewegung und ![]() -
entlang der Zugbewegung. In diesem Fall werden die Massenteilchen
parallel zur Zugbewegungsrichtung fliegen und erreichen seine Enden
gleichzeitig (allerdings nicht gleichzeitig mit dem zweiten
Teilchenpaar!). Würden wir wünschen, dass alle vier Massenteilchen
gleichzeitig die Punkte
-
entlang der Zugbewegung. In diesem Fall werden die Massenteilchen
parallel zur Zugbewegungsrichtung fliegen und erreichen seine Enden
gleichzeitig (allerdings nicht gleichzeitig mit dem zweiten
Teilchenpaar!). Würden wir wünschen, dass alle vier Massenteilchen
gleichzeitig die Punkte ![]() passieren, müssten die Basiswinkel
des Reflektors um den Winkel
passieren, müssten die Basiswinkel
des Reflektors um den Winkel 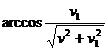 reduziert werden (falls man
einen flachen Hohlleiter anbringen würde, würde das Teilchenpaar nicht
zu hoch über dem Zug steigen, sondern würde sich parallel zu der
Zugbewegungsrichtung bewegen). Wie man sieht, die mechanischen
Analogien sind für alle mögliche Situationen möglich.
reduziert werden (falls man
einen flachen Hohlleiter anbringen würde, würde das Teilchenpaar nicht
zu hoch über dem Zug steigen, sondern würde sich parallel zu der
Zugbewegungsrichtung bewegen). Wie man sieht, die mechanischen
Analogien sind für alle mögliche Situationen möglich.
![]() und O' von Systemen
und O' von Systemen
![]() und S' aufblitzen, die sich in Bezug aufeinander mit der
Geschwindigkeit
und S' aufblitzen, die sich in Bezug aufeinander mit der
Geschwindigkeit ![]() bewegen. Zu einem Zeitpunkt
bewegen. Zu einem Zeitpunkt ![]() wird sich die Lichtfront auf der Sphäre
wird sich die Lichtfront auf der Sphäre ![]() bezüglich des Mittelpunktes
bezüglich des Mittelpunktes ![]() im System
im System ![]() und auf der Sphäre
und auf der Sphäre ![]() mit dem
Mittelpunkt O' im System S' befinden (was unmöglich scheint). Doch
braucht man sich nicht zu wundern (keine Widersprüche mit klassischer Physik),
da der Beobachter im System
mit dem
Mittelpunkt O' im System S' befinden (was unmöglich scheint). Doch
braucht man sich nicht zu wundern (keine Widersprüche mit klassischer Physik),
da der Beobachter im System ![]() das Licht mit der
Frequenz
das Licht mit der
Frequenz ![]() fixieren wird, während der Beobachter im
System S' dasselbe Licht fixieren wird, aber mit einer anderen Frequenz
fixieren wird, während der Beobachter im
System S' dasselbe Licht fixieren wird, aber mit einer anderen Frequenz
![]() (infolge des Dopplereffekts). Das sind schon zwei
identifiziert verschiedene Ereignisse: beim Treffen können die Beobachter die
Meßergebnisse
(infolge des Dopplereffekts). Das sind schon zwei
identifiziert verschiedene Ereignisse: beim Treffen können die Beobachter die
Meßergebnisse ![]() und
und ![]() immer
vergleichen!
immer
vergleichen!
![]() und O' der sich in
Bezug aufeinander bewegter Systeme
und O' der sich in
Bezug aufeinander bewegter Systeme ![]() und S' im Punkt
O=O' auslösen. Laut dem SRT legt das Licht in der Zeit
und S' im Punkt
O=O' auslösen. Laut dem SRT legt das Licht in der Zeit ![]() nach den Stunden des Systems
nach den Stunden des Systems ![]() die Entfernung
die Entfernung
![]() vom Mittelpunkt
vom Mittelpunkt ![]() zurück. In derselben Zeit
zurück. In derselben Zeit ![]() legt dasselbe Licht nach den Stunden des Systems S' die
Entfernung
legt dasselbe Licht nach den Stunden des Systems S' die
Entfernung ![]() vom Mittelpunkt O' zurück. Die Übereinstimmung der Anfangszeiten
beeinflusst die Differenz der Zeiten
vom Mittelpunkt O' zurück. Die Übereinstimmung der Anfangszeiten
beeinflusst die Differenz der Zeiten ![]() nicht
und kann sowie vor dem Experiment als auch danach mit einer beliebigen Methode
durchgeführt werden. Man kann, z.B., die unendlich entfernte periodische Quelle
verwenden, die senkrecht zur Bewegungsrichtung liegt. Man kann im voraus das
Aufblitzen nach den Stunden des Systems
nicht
und kann sowie vor dem Experiment als auch danach mit einer beliebigen Methode
durchgeführt werden. Man kann, z.B., die unendlich entfernte periodische Quelle
verwenden, die senkrecht zur Bewegungsrichtung liegt. Man kann im voraus das
Aufblitzen nach den Stunden des Systems ![]() (z.B.,
periodisch alle Million Jahre) vereinbaren, und das System S' ein
Augenblick vor dem im voraus gewählten Aufblitzen "organisieren" (im Teil 2.7
wird das damit verbundene Paradoxon der Nichtlokalität betrachtet).
(z.B.,
periodisch alle Million Jahre) vereinbaren, und das System S' ein
Augenblick vor dem im voraus gewählten Aufblitzen "organisieren" (im Teil 2.7
wird das damit verbundene Paradoxon der Nichtlokalität betrachtet).
![]() m/s bewegen. Da die
Entfernung bis zum Punkt des Aufblitzens groß ist (eine Million von
Lichtjahren), so gehen beide Beobachter in Million Jahren in die große
Entfernung
m/s bewegen. Da die
Entfernung bis zum Punkt des Aufblitzens groß ist (eine Million von
Lichtjahren), so gehen beide Beobachter in Million Jahren in die große
Entfernung ![]() m auseinander. Nach den Formeln der SRT wird die Ankunftszeit
des Signals für jeden Beobachter identisch sein. In welchem Punkt des Raumes
"versäumte" der erste Beobachter die Lichtfront für den zweiten Beobachter? Und
wenn er die Million Jahre den Spiegel gehalten und 1 Sekunde vor der
Signalaufnahme den entfernt hätte? Aus Sicht des zweiten Beobachters
reflektierte das Signal vom ersten Beobachter irgendwo vorne. Und was
reflektierte der erste Beobachter, als seine Geräte auf das Aufblitzen noch
nicht reagierten? Analog kann sich der dritte Beobachter vom zweiten mit
derselben Geschwindigkeit fortbewegen, die aber von der Quelle weg gerichtet
ist. Ob der dritte Beobachter das Licht sehen wird, wenn der zweite den Spiegel
eine Million Jahre ausschließlich eine Sekunde halten wird?
m auseinander. Nach den Formeln der SRT wird die Ankunftszeit
des Signals für jeden Beobachter identisch sein. In welchem Punkt des Raumes
"versäumte" der erste Beobachter die Lichtfront für den zweiten Beobachter? Und
wenn er die Million Jahre den Spiegel gehalten und 1 Sekunde vor der
Signalaufnahme den entfernt hätte? Aus Sicht des zweiten Beobachters
reflektierte das Signal vom ersten Beobachter irgendwo vorne. Und was
reflektierte der erste Beobachter, als seine Geräte auf das Aufblitzen noch
nicht reagierten? Analog kann sich der dritte Beobachter vom zweiten mit
derselben Geschwindigkeit fortbewegen, die aber von der Quelle weg gerichtet
ist. Ob der dritte Beobachter das Licht sehen wird, wenn der zweite den Spiegel
eine Million Jahre ausschließlich eine Sekunde halten wird?