La ley relativista para la suma de las velocidades

Recordemos que la cinemática no se ocupa de buscar las causas del movimiento, sino que afirma, por ejemplo, lo siguiente: si las velocidades están dadas, entonces se puede encontrar el resultado de la suma de las velocidades. Las cuestiones de la dinámica de partículas (ella se ocupa de las causas del movimiento) exigen un análisis a parte (ver el Capítulo 4).

Hagamos ahora una observación con respecto a la ley relativista de la suma de las velocidades. Para dos sistemas que participan directamente en el movimiento relativo no surgen dudas al determinar su velocidad relativa (ni en la física clásica ni en la TER). Supongamos que el sistema $S_2$ se mueve con relación al sistema $S_1$ a una velocidad $v_{12}$; análogamente el sistema $S_3$ se mueve con relación al sistema $S_1$ a una velocidad $v_{13}$. Prácticamente la ley relativista para la suma de las velocidades determina la velocidad relativa del aquel movimiento en el cual no participa el observador mismo. La velocidad de movimiento del sistema $S_3$ respecto al sistema $S_2$ se determina de la siguiente manera:

$$v_{23} = {v_{13} - v_{12}\over 1 - {v_{13}v_{12}\over c^2}}.$$ (1.5)

Precisamente de esta forma (aunque comúnmente se expresa $v_{13}$ mediante $v_{12}$ y $v_{23}$) se abre la verdadera escencia de dicha ley: ella dice cuál velocidad relativa de los sistemas $S_2$ y $S_3$ registrará el observador que está en el sistema $S_1$ si utiliza la regla de Einstein para la sincronización del tiempo (con ayuda de las señales luminosas) y para la medición de las longitudes. Prácticamente tenemos otra vez la "ley de la visibilidad". (Para el caso de una posible dependencia paramétrica por parte de la velocidad de la luz con respecto a la frecuencia, esta expresión será modificada. Ver los Apéndices.)

Veamos las siguientes aclaraciones metódicas. La no conmutatividad de la ley de la suma de las velocidades para los vectores no colineales es muy extraña para los conceptos cinemáticos. La propiedad de no conmutatividad (y aquello de que las transformaciones de Lorenz sin el giro no forman un grupo) se mensiona someramente sólo en algunos de los libros de texto sobre física teórica. Pero, por ejemplo, en la mecánica cuántica una propiedad semejante cambia sustancialmente todo el aparato matemático y físicamente expresa la no-mesurabilidad simultánea de las magnitudes no conmutativas.

De la ley general para la suma de las velocidades

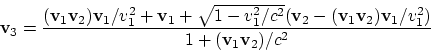$${\bf v}_3 = {({\bf v}_1{\bf v}_2){\bf v}_1/v_1^2 + {\bf v}_1... ...1{\bf v}_2){\bf v}_1/v_1^2)\over 1 + ({\bf v}_1{\bf v}_2)/c^2}$$ (1.6)

vemos que el resultado depende del orden de la transformación: por ejemplo, en el caso de la suceción

$$+v_1{\bf i}, -v_1{\bf i}, +v_2{\bf j}, -v_2{\bf j},$$

donde ${\bf i}$ y ${\bf j}$ son los vectores unitarios del sistema de coordenadas, obtenemos una velocidad sumaria nula y para otro orden de esas mismas magnitudes

$$+v_1{\bf i}, +v_2{\bf j}, -v_1{\bf i}, -v_2{\bf j}$$

obtenemos una velocidad no nula, la cual depende de manera muy complicada de las velocidades $v_1$ y $v_2$. La sucesiva aplicación de las transformaciones (del movimiento) $v_1{\bf i}$ y $v_2{\bf j}$ conducen a

$${\bf v}_3 = v_1{\bf i} + \sqrt{1-v_1^2/c^2}v_2{\bf j},$$

y en otro órde $v_2{\bf j}$ y $v_1{\bf i}$ nos llevan a

$${\bf v}'_3 = v_2{\bf j} + \sqrt{1-v_2^2/c^2}v_1{\bf i};$$

es decir, obtenemos diferentes vectores (Fig. 1.21).

Figura 1.21: El paralelogramo de velocidades en la TER.

¿Qué puede significar en este caso la descomposición del vector de velocidad en sus componentes? En primer lugar, la traslación de los métodos clásicos más simples de cómputo (el álgebra conmutativa) a las ecuaciones relativistas (no conmutativas) no es regular: incluso la solución de las ecuaciones vectoriales por componentes exige postulados adicionales, complejidades o aclaraciones. En segundo lugar, no es posible la simple aplicación de los métodos de la física clásica (el principios de las traslaciones virtuales, los métodos variacionales, etc.). Se llegaría incluso a "individualizar" el cero: la cantdad de magnitudes "nulas", constituidas por alguna combinación vectorial, deberá ser igual a la cantidad de magnitudes "nulas" constituidas por la combinación vectorial inversamente simétrica. Por consiguiente, también la teoría de las fluctuaciones necesitaría fundamentos adicionales. De este modo, contrariamente a la tesis sobre "la simplicidad y elegancia de la TER", para la fundamentación correcta incluso de los procedimientos más simples sería necesario introducir todo un conjunto de complejidades artificiales y aclaraciones (lo que no se da en los libros de texto).

Veamos la contradicción lógica de la ley relativista para la suma de las velocidades en el ejemplo del caso de una dimensión. Supongamos que tenemos una balanza en forma de ranura horizontal con un eje transversal horizontal en medio de la ranura. Por dicha ranura corren dos bolas de masa $m$ hacia diferentes lados del eje (Fig. 1.22).

Figura 1.22: La ley de la suma de las velocidades y la contradicción de la balanza.

Para evadir, por ahora, las propiedades de la masa relativista actuaremos de esta manera. Supongamos que no existe fricción en ninguna parte del eje de la balanza excepto en el punto en que ocupa la posición horizontal (el "punto muerto"). En esta posición el umbral de la fuerza de fricción no le permite a la balanza desfasarse a cuenta de la posible pequeña diferencia de las masas relativistas (entre las bolas), pero dicho umbral de sensibilidad no puede estorbar el giro de la balanza (a partir del "punto muerto") cuando falta una de las bolas (si ella se cae). Supongamos que las velocidades de las bolas en el sistema de la balanza son iguales en módulo. Entonces en este sistema las bolas rodarán al mismo tiempo hasta los extremos y caerán, de modo que la balanza quedará en posición horizontal. Veamos ahora ese mismo movimiento en el sistema en el cual la balanza se mueve a una velocidad $V$. Sea que sólo $V\rightarrow c$, pero $v\ll v_s$, donde $v_s$ es la velocidad del sonido en el material de la ranura. Entondes podemos considerar que la balanza es completamente dura (ignoramos las ondas acústicas). De acuerdo a la ley relativista para la suma de velocidades

$$v_1 = {V-v\over 1-vV/c^2}~, ~~~~~ v_2 = {V+v\over 1+vV/c^2}~.$$

El movimiento del punto medio con velocidad

$${v_1 + v_2\over 2} = V{1 - v^2/c^2\over 1 - v^2V^2/c^4} < V$$

siempre se queda atrás del movimiento de la balanza. De esta manera, en primer lugar caerá la bola que se mueve en dirección contraria al movimiento de la balanza. Como resultado, el equilibrio se romperá y la balanza empezará a girar. Tenemos una contradicción con los datos del primer observador. ¿Qué pasará con el observador si él está parado bajo la parte derecha de la balanza?

¿Pueden describir o no las transformaciones de Lorenz los pasos consecutivos de un sistema inercial a otro y responde o no la ley relativista de la suma de velocidades al cambio real de las velocidades? Por supuesto que no. Para empezar, recordemos cuál es el sentido que se introduce en la ley relativista de la suma de las velocidades. El debe demostrar que la suma de los movimientos no puede llevar a una velocidad mayor que la de la luz. ¿Cómo se pueden sumar los movimientos en ese caso? Por ejemplo, nuestra Tierra se mueve respecto a las estrellas (prácticamente existe el primer sistema de referencia en movimiento), de la Tierra despega una nave espacial a una gran velocidad (prácticamente ha sido "creado" el segundo sistema de referencia en movimiento), después, desde esta nave espacial despega el siguiente cohete (tercer sistema de referencia), etc. Precisamente esto es lo que deberá tenerse en cuenta como la aplicación sucesiva de las transformaciones. Entonces desaparece, por ejemplo, la cuestión sobre cuál velocidad es la primera, cuál la segunda en la ley de la suma de las velocidades (esto es importante para las transformaciones no conmutativas). En este sentido es en el que se dieron todos los ejemplos anteriores.

Analicemos ahora las transformaciones de Lorenz para las direcciones arbitrarias del movimiento:

$${\bf r}_1 = {\bf r} + {1\over V^2}\biggl ( {1\over \sqrt{1-V... ...\biggr ) ({\bf rV}){\bf V} + {{\bf V}t\over \sqrt{1-V^2/c^2}},$$

$$t_1 = {t + ({\bf rV})/c^2\over \sqrt{1-V^2/c^2}}.$$

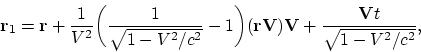
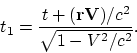
Es fácil comprobar que la aplicación consecutiva de la ley relativista de la suma de las velocidades (1.6) a los valores

$$v_1{\bf i}, ~~ v_2{\bf j}, ~~ -v_1{\bf i} - v_2\sqrt{1-v_1^2/c^2}{\bf j}$$ (1.7)

da cero. Apliquemos sucesivamente las transformaciones de Lorenz al vector arbitrario $r=x{\bf i}+y{\bf j}$ con ese mismo conjunto de velocidades. Tenemos:

$${\bf r}_1 = {x+v_1t\over \sqrt{1-v_1^2/c^2}}{\bf i} + y{\bf j},$$

$$t_1 = {t+xv_1/c^2\over \sqrt{1-v_1^2/c^2}}.$$

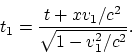
Después tenemos:

$${\bf r}_2 = {x+v_1t\over \sqrt{1-v_1^2/c^2}}{\bf i} + {y\sqr... ...xv_1v_2/c^2\over \sqrt{1-v_1^2/c^2}\sqrt{1-v_2^2/c^2}}{\bf j},$$

$$t_2 = {t+xv_1/c^2+yv_2\sqrt{1-v_1^2/c^2}/c^2\over \sqrt{1-v_1^2/c^2}\sqrt{1-v_2^2/c^2}}.$$

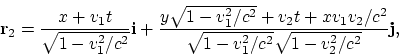
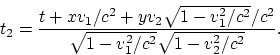
No escribiremos explícitamente las expresiones para ${\bf r}_3$ y $t_3$ a causa de su complejidad. Sin embargo, utilizando programas gráficos nos podemos convencer de las siguientes propiedades:
1) en el nuevo sistema, el tiempo inicial está desincronizado en cualquier punto del espacio exepto en el origen de coordenadas.
2) Los intervalos de tiempo cambiaron: $dt_3\ne dt$, es decir, caimos no en el sistema original en reposo, sino en un nuevo sistema en movimiento. Por consiguiente, como mínimo, en los libros de texto no se explica completamente con exactitud el sentido de las transformaciones de Lorenz o la ley relativista de la suma de las velocidades. 3) Los segmentos no sólo cambian de longitud, sino que tambien viran. Es fácil cerciorarse de esto si se encuentra numéricamente el ángulo de giro, o sea la diferencia

$$\alpha = \arctan\Biggl ( {y_3[x(1),y(1),t]-y_3[x(0),y(0),t]\over x_3[x(1),y(1),t]-x_3[x(0),y(0),t]}\Biggr ) -$$

$$- \arctan\Biggl ( {y(1)-y(0)\over x(1)-x(0)}\Biggr ) .$$

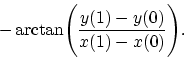
Matemáticamente se puede explicar cuantas veces se quiera estas propiedades mediante el carácter pseudoeuclidiano de la métrica, pero fisicamente todo es muy fácil. Estas propiedades demuestran el carácter no objetivo (sino sólo aparente) de las transformaciones de Lorenz y de la ley relativista de la suma de las velocidades y la discordancia entre ellas. Efectivamente, puesto que pasamos consecutivamente de un sistema inercial a otro y el giro significa la no-inercialidad del sistema, entonces la TER se sale ella misma de los límites de su propia aplicación, es decir, es contradictoria. Si este giro fuese real, esto significaría la no objetividad del concepto de sistema inercial (ya que el resultado dependería del método de transición a dicho sistema) y, como consecuencia, significaría también la ausencia de los fundamentos mismos para la existencia de la TER.

Intentemos pues enteder por qué las interpretaciones de los libros de texto nos llevan a la discordancia de las dos expresiones: de la ley relativista de la suma de las velocidades y de las transformaciones de Lorenz, a pesar de que la primera expresión se obtiene de la segunda. Recordemos esta deducción mediante el ejemplo del movimiento mutuo unidimensional de los sistemas $K$ y $K'$. Partiendo de las transformaciones de Lorenz

$$x_1 = {x+Vt\over \sqrt{1-V^2/c^2}}~, ~~~~ t_1 = {t+Vx/c^2\over \sqrt{1-V^2/c^2}}$$

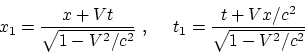
dividamos los diferenciales $dx_1$ por $dt_1$ considerando las definiciones $v=dx/dt$ y $v_1=dx_1/dt_1$ y obtenemos:

$$v_1 = {v+V\over 1+vV/c^2}.$$

De aquí se ve lo siguente:
1) el observador se encuentra en el centro del sistema $K$ y mide la distancia $x$ hasta el cuerpo estudiado en sus sistema $K$.
2) él considera el tiempo $t$ como único en su sistema y determina la velocidad del cuerpo en su sistema $v=dx/dt$.
3) él mide la velocidad $-V$ del sistema $K'$ con relación al sistema $K$ utilizando su propio (!) tiempo $t$ y considera que las velocidades relativas de los sistemas son mutuamente reversibles respecto a la dirección.
Este observador no puede medir niguna otra cosa más: el valor resultante de la velocidad $v_1$ es el valor calculado. De esta manera, llegamos a la interpretación [49] expuesta anteriormente: La ley relativista de la suma de las velocidades determina la velocidad de aquel movimiento relativo en el cual no interviene el propio observador. Este efecto no es real, sino sólo aparente (cuando utilizamos las reglas determinadas de la TER). Según la escencia de la fórmula no podemos simplemente pasar a la segunda sustitución para definir $v_2$, aunque formalmente en la expresión de la ley relativista de la suma de las velocidades se pueden sustituir susecivamente cuantos valores de las velocidades se quiera. En el caso de la suma de los movimientos a lo largo de una recta la propiedad clásica de conmutatividad se conserva y la contradicción resulta velada. Pero si los vectores de las velocidades no son colineares, entonces el punto 3) resulta ser falso e inmediatamente aparece la contradicción y la discordancia entre la leye de la suma de las velocidades y las transformaciones de Lorenz.

En el ejemplo analizado anteriormente se puede proceder de otra manera: busquemos una sucesión de tres transformaciones de la velocidad que conserve inmutable el tiempo inicial en las transformaciones de Lorenz. Es fácil, entonces, comprobar que en lugar de (1.7) se puede tomar una sucesión única:

$$v_1{\bf i}, ~~ v_2{\bf j}, ~~ -v_1\sqrt{1-v_2^2/c^2}{\bf i} - v_2{\bf j} .$$ (1.8)

Sin embargo, en primer lugar, el giro del segmento permanece. En segundo lugar, el nuevo conjunto de velocidades no satisface en dicha suceción la ley de suma de las velocidades, es decir, prácticamente se cambió el orden de sustitución de las velocidades $v_1$ y $v_2$ en la ley de la suma de las velocidades (lo que no corresponde a la escencia de esta ley). De esta manera, las contradicciones tampoco se eliminan. Una de las manifestaciones de la contradicción de la TER es la precesión de Thomas: partiendo de la sucesión de los sistemas inerciales (que se mueven de forma rectilínea y uniforme) a final de cuentas resulta, repentínamente, que el objeto ha realizado un giro (un movimiento categóricamente no inercial). De este modo, la transición desde las transformaciones de Lorenz en el " espacio matemático" 1+1 ($t+x$) expuestas en los libros de texto típicos hacia las transformaciones de Lorenz en el " espacio" 1+2 o 1+3 contiene contradicciones físicas.

Muchas propiedades de las magnitudes físicas que son intuitivamente comprensibles pierden su sentido en la TER. Por ejemplo, la velocidad relativa deja de ser invariante. Las partículas que vuelan a lo largo de una misma recta a difernetes velocidades forman en la TER un complejo " abanico de velocidades" para un sistema en movimiento. En la TER la distribución isotrópica por velocidades deja de ser tal para otro sistema en movimiento. No hay, en realidad, ninguna simplificación tal en la TER.

De la TER no resulta en absoluto la imposibilidad de la existencia de velocidades $v>c$. Y la adición de que esto se refiere sólo a la velocidad de transmisión de la señal es artificial (en vista de la existencia de contraejemplos evidentes respecto a la interpretación difundida). No obstante, incluso con tal adición noqueda aun suficientemente determinado el concepto de señal (información). Por ejemplo, al obtener la señal del destello de una supernova ¿acaso no estamos seguros de que tal información tambiés "se tiene" a la distancia diametralmente opuesta respecto a la supernova, es decir, nosotros sabemos esto a una velocidad $2c$? ¿O esto no es información? Por lo tanto, en la TER se puede tener en mente sólo la información que está en un portador material de naturaleza electromagnética y que se desplaza en el vacio consecutivamente a través de todos los puntos del espacio desde la fuente hasta el receptor de la señal.

Hagamos una aclaración con respecto a la "maravillosidad" de la ley relativista de la "suma" de las velocidades, que permite intercambiar señales de luz incluso cuando la suma algebraica de las velocidades resulta mayor a $c$. Prestemos atención a un hecho evidente: las señales para el intercambio de información deben enviarse necesariamente hacia la dirección del objeto y no hacia la dirección contraria. Por eso no hay nada impresionante en el intercambio de señales cuando, incluso en el caso clásico, como resultado de la suma formal de las velocidades resulta que $v_1+v_2>v_{se}$. Sea que dos aviones despegan del aeródromo $O$ con velocidades $0,9v_{so}$ y se separan uno del otro hacia direcciones opuestas al eje $X$ (o sea, a una velocidad relativa $1,8v_{so}$). ¿Es posible entre ellos el intercambio se señales sonoras? ¡Por supuesto! Puesto que la onda sonora se transmite en el aire independientemente de la velocidad de la fuente $S_1$ en el momento de envío de la señal, entonces el primer avión (el que ha enviado la señal) alcanzará al frente de onda, que se desplaza hacia la dirección positiva del eje $X$, y el segundo avión "competirá" con el frente de onda, que se desplaza hacia la dirección negativa del eje $X$. Ambos aviones se mueven más lentamente que los correspondientes segmentos de frente de onda más cercanos a ellos (Fig. 1.23).

Figura 1.23: El intercambio de señales.

De esta manera, la suma de las velocidades en realidad se equipara (de forma compleja) no con la velocidad del sonido, sino con el valor $2v_{so}$ (y para la luz con una velocidad $2c$).

Es evidente que la restricción física al valor de la velocidad no puede atribuirsele a las matemáticas (el hecho de que en algunas expresiones bajo el símbolo del radical exista un valor negativo). Simplemente hay que recordar que todas las fórmulas de la TER se han obtenido utilizando el intercambio de señales luminosas (el método de sincronización de Einstein). Si el cuerpo inmediatamente se mueve a una velocidad superior a la de la luz, entonces la señal enviada tras él simplemente no podrá alcanzarlo. De la misma manera se puede introducir la sincronización con ayuda del sonido (e igualmente habrá particularidades en las fórmulas) pero de aquí no se seguirá en absoluto la imposibilidad de las velocidades ultrasónicas. La velocidad de transmisión de las perturbaciones (sonoras o luminosas) en el medio no estará de ninguna manera ligada a la velocidad del movimiento de cierto cuerpo a través de este medio.