Принцип Маха

Принцип Маха обусловленности инертной массы и абсолютности ускорения действием далеких звезд также сомнителен, так как объясняет внутренние свойства одного тела через свойства других тел. Конечно, идея сама по себе красивая. Если считать, что все в мире взаимосвязано и существует некоторое идеальное полное уравнение состояния, то любое свойство тел должно определяться влиянием всей остальной Вселенной. Однако, тогда пришлось бы каждую частицу считать индивидуальной. Этот путь порочен для науки, идущей от меньшего знания к большему, так как "нельзя объять необъятное". Практически, если учесть неравномерное распределение массы (в компактных объектах) и разные величины сил притяжения от ближних и дальних объектов, то получилось бы сплошное "дерганье" вместо равномерного вращения или равномерного движения по инерции.

Принципиально принцип Маха не может быть проверен: как удаление всех тел из Вселенной, так и искусственное устремление гравитационной постоянной к нулю - ничего не имеющие с реальностью абстракции. Однако, экспериментально можно оценить влияние "далеких звезд", считая массу Вселенной сосредоточенной в основном в компактных объектах. Сила притяжения звезды с массой порядка массы Солнца $M\sim 2\cdot 10^{30}$ килограмм, находящейся на расстоянии в 1 световой год $\sim 9\cdot 10^{15}$ метров эквивалентна действию груза массой всего $m_0\sim 25$ грамм находящегося на расстоянии 1 метр. Воспользуемся пока сомнительной теорией Большого взрыва и будем считать время существования Вселенной $\sim 2\cdot 10^{10}$ лет. Даже если бы звезды разлетались со световой скоростью мы имели бы размеры Вселенной $\sim 2\cdot 10^{10}$ световых лет. Считаем среднее расстояние между ближайшими звездами 1 световой год. Мы намеренно увеличиваем все величины, например, массу Вселенной и ее плотность $\rho\sim 10^{33}/10^{54} \sim 10^{-21}$ г/см$^3$. Учтем теперь, что при удалении тел друг от друга вдвое, сила уменьшается вчетверо и т.д.. Попробуем имитировать силу воздействия всей Вселенной в некотором направлении. Даже если считать среднее расстояние между ближайшими звездами в 1 световой год, то на расстоянии в 1 метр нужно поместить массу в граммах (суммируем до $2\cdot 10^{10}$)

$$M_0\sim 25(1+1/4+1/9+\cdots) = 25\sum 1/n^2\sim 25\pi^2/6 < 50.$$

Фактически коэффициент $\pi^2/6$ выражает некоторое эффективное увеличение плотности на линии наблюдения. Для имитации действия "всей Вселенной" можно взять толстую металлическую сферу с внешним радиусом 1 метр и толщину в направлении к центру сделать переменной (можно даже для имитации неоднородностей сделать игольчатую структуру вблизи внутреннего радиуса).

Пусть толщина сплошной сферы $0,6$ метра, то есть от центра до $0,4$ метра - ниша, а далее до 1 метра - металл. Тогда массе $M_0$ при плотности $\sim 8,3$ г/см$^3$ будет соответствовать цилиндрический столбик радиусом $\sim 0,35$ см. В реальности мы должны учесть влияние звезд в конусе, а не только в цилиндре. Хотя мы также имеем шаровой металлический конус, тем не менее оценим порядки величин. Разобьем конус на цилиндрические слои, возникающие по мере вовлечения новых слоев звезд (Рис. 2.9).

Рисунок 2.9: Принцип Маха и влияние Вселенной.

Каждый новый слой будет больше предыдущего слоя на 6 звезд. Расстояния от центра до ближайшей границы каждого слоя звезд можно найти из подобия треугольников: $R_i/1 = i/r$. Тогда имеем $R'_i = \sqrt{i^2(1+r^2)}/r$. Следовательно, поправка к массе $M_0$ (суммируем до $2\cdot 10^{10}$) найдется как

$$m_0(1+{1\over 4}+\cdots )\biggl ( 1 + \sum_i {6\over {R'}_i^2}\biggr ) < M_0\biggl ( 1+ 6r^2 \sum_i {1\over i}\biggr )$$

$$\sim M_0\biggl ( 1 + 6 \cdot 10^{-5} \log{(2 \cdot 10^{10})}\biggr ) \sim M_0(1+0,02).$$

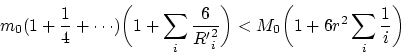
Таким образом, нашей конструкции с лихвой хватает для учета действия "всей Вселенной". Конечно, если Вселенная бесконечна, то полученный гармонический ряд разойдется и конструкция будет неадекватна. Однако это противоречит как ОТО, так и современным взглядам и наблюдательным данным.

Поместим теперь внутрь сферы шарики на пружине. Для избежания побочных эффектов воздух можно из конструкции откачать и дополнительно изолировать шарики от сферы тонким сосудом. Если начать вращать сферу, то согласно принципу Маха должна появиться центробежная сила и шарики разойдутся. При этом центробежная сила должна быть такой же, как если бы вращались сами шарики. Кажется вполне очевидным, что это невозможно, так как такой эффект был бы давно замечен. Таким образом, мы возвращаемся к абсолютным понятиям ускорения, массы, пространства и времени, определенным еще Ньютоном. Однако описанный опыт мог бы оказаться полезным для определения поправок к статическому закону тяготения Ньютона. При этом шарики должны иметь достаточную свободу передвигаться и вращаться, так как неизвестно заранее направление действия поправочных сил и моментов сил.