Le principe de Makh

Le principe de Makh du conditionnement de la masse inerte et du caractère absolu de l'accélération par l'action des astres lointains est aussi douteux, parce qu'il explique les particularités intérieures d'un corps par des particularités des autres corps. Il est évident, que l'idée elle-même est belle. Si on suppose que tous dans le monde est lié et qu'il existe une certaine équation d'état complète et idéale, n'importe quelle particularité des corps doit être déterminée par l'influence du reste de l'Univers. Pourtant, si on le supposait il faudrait considérer chaque particule comme individuel. Cette voie est vicieuse pour la science qui se développe des connaissance minimes aux connaissances plus importantes, parce qu' "à l’impossible nul n'est tenu"? Du point de vue pratique, si on prend en compte l’inégalité des masses (dans des volumes compacts) et des quantités différentes des forces de l'attraction des objets proches et lointains, on aurait un "tic" total au lieu de la rotation égale ou le mouvement égal par inertie.

Le principe de Makh ne peut pas être vérifié par principe: et l'élimination de tous les corps de l'Univers, et l'aspiration artificielle de la constante gravitationnelle à zéro sont des abstractions n'ayant rien de commun avec la réalité. Pourtant on peut évaluer l'influence des "astres lointains" d'une manière expérimentale, estimant la masse de l'Univers concentré en général dans des objets compacts. La force d’attraction d'un astre avec la masse au celui du Soleil $M\sim 2\cdot 10^{30}$ kilogrammes, se trouvant à la distance d'une année-lumière $\sim 9\cdot 10^{15}$ mètres près, est équivalente à l'action d'un chargement avec la masse $m_0\sim 25$ grammes se trouvant à la distance égale à 1 mètre. Utilisons pour le moment de la théorie douteuse de la Grande Explosion et estimons le temps de l'existence de l'Univers égal à $\sim 2\cdot 10^{10}$ d'ans. Même si les astres se dissipaient avec la vitesse de la lumière, les dimensions de l'Univers seraient $\sim 2\cdot 10^{10}$ d'années-lumière. Supposons que la distance moyenne entre les astres les plus proches, soit 1 année-lumière. Nous augmentons sciemment toutes las quantités, par exemple la masse de l'Univers et sa densité $\rho\sim 10^{33}/10^{54} \sim 10^{-21}$ g/cm$^3$. Notons maintenant que lors de l'éloignement des corps l'un d'un autre en deux fois, la force se réduit de quatre fois etc. Essayons d'imiter la force d'influence de tout l'Univers dans une certaine direction. Même si on estime la distance moyenne entre les astres les plus proches égale à 1 année-lumière, il faut mettre la masse en grammes (résumons jusqu’à $2\cdot 10^{10}$) sur la distance d'un mètre

$$M_0\sim 25(1+1/4+1/9+\cdots) = 25\sum 1/n^2\sim 25\pi^2/6 < 50.$$

En effet le coefficient $\pi^2/6$ exprime une certaine augmentation de la densité sur la ligne d'observations. Pour l'imitation de l'action de "tout l'Univers" on peut prendre un gros sphère métallique au rayon extérieur d'1 mètre et faire l'épaisseur en direction du centre variable (et pour imiter des hétérogénéité on peut créer une structure aciculaire tout près du rayon intérieur).

Supposons que l'épaisseur d'une sphère unie, soit $0.6$ mètres, c'est-à-dire $0.4$ mètres du centre représentent une niche, et puis jusqu’à 1 mètre - du métal. Alors la masse $M_0$ avec la densité $\sim 8.3$ g/cm$^3$ correspondra à une colonne cylindrique d'un rayon de $\sim 0.35$ cm. En réalité nous devons prendre en compte non seulement l'influence des astres dans le cylindre, mais aussi dans le cône. Bien que nous ayons aussi un cône sphérique métallique, évaluons des degrés des quantités. Divisons le cône aux couches cylindriques, apparaissant au fur et à mesure de l'engagement de nouvelles couches des astres (Figure 2.9).

Figure 2.9: Le principe de Makh et l'influence de l'Univers.

Chaque nouvelle couche sera plus épaisse que la précédente à 6 astres. On peut trouver la distance entre le centre et la limite la plus proche de chaque couche, en partant de la similitude des triangles: $R_i/1 = i/r$. Alors, on a $R'_i = \sqrt{i^2(1+r^2)}/r$. Alors, la correction de la masse $M_0$ (résumons jusqu'à $2\cdot 10^{10}$) se déterminera comme

$$m_0(1+{1\over 4}+\cdots )\biggl ( 1 + \sum_i {6\over {R'}_i^2}\biggr ) < M_0\biggl ( 1+ 6r^2 \sum_i {1\over i}\biggr )$$

$$\sim M_0\biggl ( 1 + 6 \cdot 10^{-5} \log{(2 \cdot 10^{10})}\biggr ) \sim M_0(1+0,02).$$

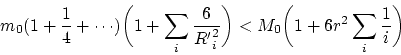
Donc, cette construction suffit pour enregistrer l'action de "tout l'Univers" et bien au-là. Il est sur que si l'Univers est infini, la série harmonique reçue se dissoudra et la construction ne sera pas adéquate. Pourtant cela contredit et à la TRG, et aux opinions contemporaines, et aux données observées.

Et maintenant mettons à l'intérieur d'une sphère des bulles à ressort. Pour éviter des effets secondaires il faut pomper l'air dans la construction et isoler aussi les bulles de la sphère par un vaisseau aux murs fins. Si on commence à tourner la sphère, selon le principe de Makh, la force centrifuge doit apparaître et les bulles s'éloigneront. Avec cela la force centrifuge doit être la même, comme si les bulles eux-mêmes se tournaient. Il semble évident que cela est impossible, parce qu'un tel effet serait remarqué déjà. Donc, nous revenons aux concepts absolus de l'accélération, de la masse, de l'espace et du temps, définis encore par Newton. Pourtant l'expérience décrite pourrait être utile à la détermination des corrections de la loi statique de la gravité de Newton. Avec tout cela les bulles doivent avoir la liberté du mouvement et du tournant, car la direction de l'action des forces correctives et des moments des forces ne peut pas être connue d'avance.