The universal absolute time

The notion of time is broader, than the dimensional factor in transformation laws, and bears much greater relation to the local irreversibility of processes. First, a single-valued "binding" of time to the motion of a body does not take into account internal processes, which can be anisotropic, pass at various "rates" and characterize the local irreversibility (each such rate is in different manner added geometrically with the velocity of a body as a whole). Second, the binding of time only to the velocity of transmission of electromagnetic interactions does not take into account other possible interactions (which can propagate in vacuum) and actually implies electromagnetic nature of all phenomena (the absolutisation of electromagnetic interactions). Later we shall consider, how the universal absolute time can be introduced.

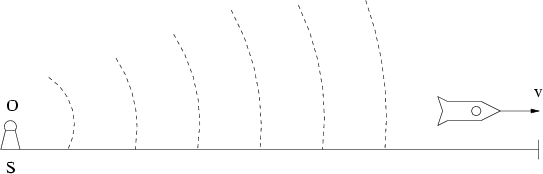
When we introduce the notion of intrinsic time (actually, subjective time), the following methodological point seems important: We should not calculate intrinsic time of an alien object according to our own rules, but rather "ask" this object itself. Consider the following experiment (Fig. 1.8):

Figure 1.8: The interchange of signals of intrinsic time.

Let an observer be situated in the motionless system $S$ at point $O$, where a beacon is installed. The beacon flashes each second (as a result, the number of flashes $N$ equals the number of seconds passed at point $O$). Let an astronaut (in moving system $S'$) be launched from point $O$. Then, when moving away from point $O$ the astronaut will perceive flashes more rarely (at lower frequency), than before launching (in fact, beacon's "time slowing" takes place). But upon approaching to the beacon the astronaut will see the opposite, flashes will occur more frequently than before launching (now we have beacon's "time speed-up"). For $v < c$ it is obvious that the astronaut can neither outstrip any flashes, nor go around any of flashes (light spheres). So regardless of his motion schedule and trajectory, upon returning to point $O$ the astronaut will perceive equally $N$ flashes total, i.e. all flashes, which have been emitted by a beacon. Therefore, each of these two observes will confirm that $N$ seconds have passed at the beacon.

If the astronaut on board the spacecraft will also have a beacon and will signal about the number of seconds passed on his watch, then no disagreements will arise concerning astronaut's time as well. The situation appears to be fully symmetrical (for the twins paradox, for example). When meeting at the same point, all light spheres will intersect opposite observers (their quantity can neither increase, no decrease). This number is equal to $N$ - the number of seconds passed for both observers.

Consider now the problem of establishing the universal absolute time. (Of course, if we measure the time by beatings of our own heart, it will be subjective and will depend on the internal and external conditions). The attempt to introduce individual "electromagnetic time" and to absolutize it - this is a return to the past. However, even at that time the people could synchronize time, despite miserable data transmission rate (by pigeon-post, for example), because they used a remote source of signals (the Sun or stars). Let us imagine the following mental experiment (Fig. 1.9).

Figure 1.9: An infinitely remote source for establishing unified absolute time.

The remote source $S$, which lies on a middle perpendicular to segment $AB$, sends signals periodically (with period $T$). At the time of signal arrival to point $O$, two recording devices ($1$ and $2$) begin to move mirror-symmetrically (at velocities ${\bf v}$ and $-{\bf v}$), while reflecting from $A$ and $B$, with period of $2T$. Velocity $v$ can be arbitrary (we can choose the appropriate distance $\vert AB\vert$). In spite of the fact, that at each time instant the devices are moving relative to each other at speed $2v$ (except the reflection points), the signals will be received at the same time, namely, at the time of passing by point $O$ (observer $3$ can be placed at this point). The time, determined in such a manner, will be universal (at point $O$), i.e. the same for all three observers. In order to make the following step, we note that for deriving the transformation formulas in the SRT, it is sufficient to consider the relative motion along a single straight line (since the systems are inertial). By choosing the large distance $\vert SO\vert$ we may assure that the time difference between signal arrival to point $O$ and to points $A$ and $B$ be smaller than any pre-specified value. As a result, to the given accuracy the time will be the same for the whole chosen segment $AB$ regardless of the velocities of motion of observers $1$ and $2$. Thus, the infinitely remote source of signals, situated perpendicular to the direction of relative motion of systems, can serve as a watch counting the universal absolute time (which is the same regardless of the inertial system of reference). The question on the change in the observed direction of signal arrival will be presented below lest a temptation are going to arise in "far-fetched" use of the aberration allegedly demonstrating the change in the wave front direction.