Some relativistic solutions and corollaries

Consider now a paradox of transformation of forces. Let we have two charges $e_1$ and $e_2$ of opposite sign, which are at rest and separated by two parallel planes being at distance $L$ apart of each other (see Fig. 4.4).

Figure 4.4: Paradox of transformation of forces.

Owing to attraction to each other, the charges are at a minimum distance $L$ from one another. (They are at the state of neutral equilibrium with respect to a system of planes.) We shall draw a mark on a plane under each charge, or we shall place the observers nearby. Now we shall observe this system of charges from a relativistic missile moving at velocity ${\bf v}$. Let $\theta$ be the angle between vectors ${\bf v}$ and ${\bf L}$. Determining the electromagnetic forces, acting between these charges in missile's frame of reference [17], we shall be interested in tangential components of forces, i.e. in the components of forces along the planes. The force influencing charge $e_1$ is

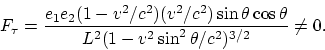$$F_{\tau} = {e_1e_2(1-v^2/c^2)(v^2/c^2)\sin\theta\cos\theta\over L^2(1-v^2\sin^2\theta/c^2)^{3/2}}\ne 0.$$ (4.1)

Therefore, the charges will be displaced from their initial position. Let the balls be having huge charges, $L$ be small ($L\rightarrow 0$), and $v$ be large ($v\rightarrow c$). Let the observers to retain the balls with very thin threads. Whether they will be torn? The answer depends on the system of observation. So, who of the observers will be right? Thus, we have another inconsistency of SRT.

Let us consider now some particular problems. Methodically paradoxical is the description of motion of charged $e$ particle of mass $m_0$ in the constant uniform electric field $E_x=E$ (see [34]). Really, in the classical physics the trajectory for $v_y=v_0$ is parabola $x=eEy^2/(2m_0v_0^2)$, and in SRT it is the chain line

$$x = {m_0c^2\over eE}\biggl ( \cosh\biggl [ {eEy\over m_0v_0c}\biggr ] - 1\biggr ).$$

But for large $y$ values the relativistic trajectory is close to an exponential curve, i.e. it is steeper, than parabola. But what in this case we should do with the idea on increasing the inertia (mass) of a body with the velocity? Even if we suppose that, despite a slightly greater steepness, the particle is slower moving over the trajectory, then due to which forces it has been slowed down over axis $y$? You see, force $F_y=0$, and it will not appear in SRT as well: $F'_y=0$. And the initial velocity value $v_y=v_0$ can be non-relativistic (and will remain the same).

Strange is the energy balance for a relativistic missile [33]:

$$m\cosh\theta + M_2\cosh(d\theta) = M_1.$$

At high ejection rate ($\theta=\tanh(v/c)$) for finite values of initial $M_1$ and final $M_2$ masses the following condition (for SRT consistency) should be fulfilled: the mass of a separate ejection $m\rightarrow 0$. However, this quantity is determined by technological design of the rocket only: there are no principal limitations.

One of derivations of Einstein's relation $E=mc^2$ is insufficiently substantiated. The process of absorption of two symmetrical light pulses by a body in this derivation is considered from the viewpoint of two observers moving relative to each other. The first observer is resting relative to a body and the second one is moving perpendicular to the light (Fig. 4.5).

Figure 4.5: To the derivation of the formula $E=mc^2$.

It occurs in SRT that the light should "know" beforehand about observer's motion at velocity $v$ exactly, and the momentum should be received in such a manner, that in this second system the velocity of a body be not changed, and only its mass could change. But in such a case what shall we do with Lebedev's experiments (and to the present conventional concepts) on light pressure, where at momentum transmission by light it was the observed velocity of a body, which has changed? And what will happen to the momentum, if we shall have absolutely absorbing rough (skewed) surfaces? It is also unclear from presented drawings, whether we are dealing with real transversal light (the model, which now is conventional, including in the SRT as well) or with some mystical longitudinal-transversal light (for "saving" SRT).

Rather strange in the modern version of the SRT is the difference in the cumulative radiation mass as a dependence on system's momentum:

$$m = \sqrt{{(E_1+E_2)^2\over c^4} -{({\bf P}_1+{\bf P}_2)^2\over c^2}}.$$ (4.2)

And if we shall change the momentum (direction) of separate photons by mirrors? In this case we shall determine the center of gravitation of a system. Where will it be localized also what will be the structure of the field closely to it? Will this center be skipping, disappearing and appearing, really? Let us make use of presented SRT formula (4.2) for determining the mass of cumulative radiation of two photons, flying apart of each other at arbitrary angle, and consider the radiation diverging from the same center (see Fig. 4.6).

Figure 4.6: An indefinite mass of the photon combination.

Then, depending on the in-pair grouping of photons, we can obtain different cumulative mass of the whole system (whether will it be necessary to introduce artificially the negative masses for "explaining" all possible variations of a mass?). And in GRT it is necessary to take into account the radiation birth prehistory for determining the localization of its center of gravitation and, besides, to take into account the whole unknown space-time structure of the electromagnetic field for correct description of quite different a phenomenon - the gravitation. Infinitely complicated procedure, really!