Energy and momentum in SRT

We begin with a comment concerning the units of measurement. The expression for the momentum and energy in terms of a mass can not give anything useful, since these quantities are not interchangeable, the number of joint operations with them (as well as combinations) is limited and, all the same, it is necessary to monitor them as various physical quantities. Whether is it worth to introduce confusion into well-agreed units of dimensions?

Whether the SRT approach to the relativistic dynamics is a unique one? Not at all! In the classical physics the separation of energy into kinetic and potential ones can be rather conventional. For example, in the statistical physics at description of motion in non-inertial rotating systems the potential energy includes, in fact, the mean kinetic (!) energy of motion of a system: from $v_{\varphi}=\Omega\rho$ is generated $E_{pot}=m\Omega^2\rho^2/2$. There exists another educative example from the hydrodynamics, where the apparent ("effective") mass concept is introduced for describing the motion of a body through a medium. The true mass did not obviously change in this case. In exactly the same manner, in the relativistic mechanics a new "velocity" addition to the acceleration can be associated with the potential energy of a body. In this case the kinetic energy of a body can be retained invariable, and the classical Newtonian equations can be considered, but with other, "effective" force and constant mass $m_0$.

Contrary to the SRT assertions on the importance and necessity of introducing the 4-dimensional vectors, even for three interacting particles the expressions

$$E = \sum_i m^{(i)}c^2\gamma^{(i)}, ~~~ {\bf P} = \sum_i m^{(... ... ~~ \mbox{where} ~ \gamma^{(i)} = {1\over \sqrt{1-v_i^2/c^2}}$$

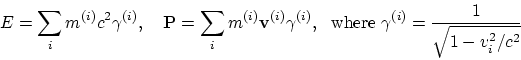
do not constitute the 4-dimensional vectors and are not conserved. The introduction of the potential energy of interaction of particles also causes some difficulties. Is SRT a theory of two bodies, really? Where is the declared generality (universality) of the theory? Similar difficulties arise in constructing the Lagrangian and Hamiltonian functions for systems of interacting particles.

A limiting transition to the classical energy is contradictory too. Above we have considered the condition of such a transition: $c\rightarrow\infty$. But in such a case not only the energy of rest, but any other energy will be $E=\infty$ in SRT. Not consistent is also the expression for the relativistic momentum in the form of [26]: ${\bf P}=m{d{\bf r}/d\tau}$, since $d{\bf r}$ relates to the motionless frame of reference, and $d\tau$ (the intrinsic time) relates to the moving system (i.e. to a body).

The limiting transition to low velocities also raises a series of questions. All formulas should pass to the Newtonian form where the rate of transmission of interactions is supposed to be infinite (for example, the Lagrangian function, the action, the energy, the Hamiltonian function, etc.). We see, however, that this is not the fact [17]: the four-velocity transfers into a set of four numbers (1,0,0,0) and does not mean anything, the same is true for the four-acceleration; the interval $S\rightarrow\infty$, and quantity $dS$ depends on the order of limiting transition; the four-force components tend to a zero, etc. This clearly indicates, that all aforementioned quantities cannot have independent physical sense.