The geometry of space

The question on the change of real space geometry in GRT is fully aberrant. The finiteness of the rate of transmission of interactions can change only physical, but not mathematical laws. Whether shall we assert, that the straight line does not exist, only because its drawing into infinity, even at light speed, will require infinite time? (The same is true for the plane and space). The mathematical sense of derivatives can not change as well. One of GRT demonstrations "on the inevitability of the change of geometry in the non-inertial system" is as follow: in the rotating coordinate system, due to contraction of lengths, the ratio of the length of a circle to its diameter will be lower, than $\pi$. Note that nobody can draw a "new geometry" for this case: "non-existing" cannot be pictured. In fact, however, not only the true, but even the observed geometry will not change: whether the mathematical line will move or change as we move? Although the radius, which is perpendicular to the circle motion, must be invariable, nevertheless, we suppose at first, that the circle will move radially. Let we have three concentric circles of almost the same radius (Fig. 2.1).

Figure 2.1: The geometry of a rotating circle.

We place the observers on these circles and number them in the order from the center: 1, 2, 3. Let the second observer be motionless, whereas first and third ones are rotating around center $O$ clockwise and counter-clockwise at the same angular velocity. Then, owing to the difference in relative velocities and contraction of lengths, the observers will interchange their places. However, when they happen to be at the same point of space, they will see different pictures. Indeed, the 1-st observer will see the following position from the center: 3, 2, 1, whereas the 2-nd observer will see the different order: 1, 3, 2, and only the 3-rd observer will see the original picture: 1, 2, 3. So, we have a contradiction. Suppose now, that the geometry of a rotating plane has changed. However, what will be more preferable in such a case: the top or the bottom? The problem is symmetric, in fact; to what side the plane has curved in such a case? If we make the last supposition, that the radius has curved (as the apparent motion changes in the non-inertial system), then the second observer will see it as non-curved, whereas the first and third observers will consider it as "curved" to different sides. Thus, three observers will see different pictures at the same point for the same space; therefore, the curvature of the radius is not an objective fact (and cannot be a matter for scientific enquiry).

The rotating circle proves the contradictive nature of SRT and GRT ideas. Really, according to the textbooks, the radius, which is perpendicular to the motion, does not change. Therefore, the circles will remain at their places irrespective of the motion. Let us seat the observers on a motionless circle at equal distances from each other and produce a point-like flash from the center of a circle, in order the observers to draw the strokes on a moving circle at the time of signal arrival (Fig. 2.2).

Figure 2.2: Equidistant observers at a circle.

Owing to the symmetry of a problem, the strokes will also be equidistant. At subsequent periodic flashes (with the appropriate period) each observer will confirm, that a stroke mark passes by him at the flash instant, that is, the lengths of segments of motionless and rotating circles are equal. When the circle stops, the marks will remain at their places. The number of equidistant marks will not change (it equals to the number of observers). Therefore, the lengths of segments will be equal in the motionless case as well. Thus, no contraction of lengths (and change of geometry) took place at all.

Now we consider again the space geometry problem, but with the other approach. This problem is entirely confused still since the times of Gauss, who wanted to determine the geometry with the help of light beams. The limited nature of any experiment cannot influence the ideal mathematical notions, does it? Note, that in GRT the light even moves not along the shortest path: instead of Fermat's principle $\delta\int dl = 0$, we have in GRT [17]: $\delta\int (1/\sqrt{g_{00}})dl = 0$, where $g_{\alpha\beta}$ is metric tensor. What does distinguish the light in such a case? The necessity of changing the geometry is often "substantiated" in textbooks as follows: in order the light to "draw" a closed triangle in the gravitational field, the mirrors should be turned around at some angle; as a result, the sum of angles of a triangle will differ from $\pi$. However, for any point-like body and three reflectors in the field of gravity (see Fig. 2.3) the sum of "angles" can be written as:

$$\sum\beta_i = \pi + 4\arctan{\Biggl ( {gL\over 2v_0^2}\Biggr ) } - 2\arctan{\Biggl ( {gL\over v_0^2}\Biggr ) }.$$

Figure 2.3: "Geometry of a triangle".

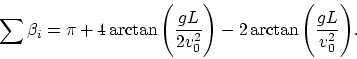
It occurs, that the geometry of one and the same space depends on the conditions of the experiment: on $L$ and $v_0$. Since the angle $\alpha$ between the mirrors $A$ and $B$ can also be changed (we chose $\alpha=0$ in our Fig. 2.3), we have a possibility of artificial changing the geometry within wide limits. Note, that the same variable parameters $\alpha$ and $L$ remain for the light as well. In such "plausible" proofs of the necessity of changing the geometry some important points are not emphasized. First, both in the experiment with material points, and in the experiment with the light the geometry is "drawn" sequentially during some time, rather than instantaneously. Second, for accelerated systems the particles (and the light) move in vacuum rectilinearly, according to the law of inertia, and, actually, the motion of the boundaries of this accelerated system is imposed on this motion additively. All angles of incidence (in the laboratory system) are equal to corresponding angles of reflection, and the "geometry of angles" does not change at all. Simply, the figure is obtained unclosed because of motion of the boundaries. Third, the role of the boundaries is not uncovered at all in determining the relations between the lengths of real bodies. For example, if all points of a real body are subject to the effect of identical accelerating force, then the mutual relation between lengths and angles (the "geometry") remains unchanged. If, however, only the boundaries are subject to acceleration, then all real changes of bodies' size take place only at interaction with the boundaries. In any case the Euclidean straight lines can be drawn. For example, to draw the horizontal straight line in the gravitational field we take two similar long rods (Fig. 2.4).

Figure 2.4: Drawing of the straight line in the gravitational field.

At the middle of the first rod we install a point-like support. As a result of bending of a rod, the upward-convex line is generated. Then we install two point-like supports for the second rod at the level of two lowered ends of the first rod. As a result of bending of the second rod, the downward-convex line is generated. The middle line between these two bonded rods determines the straight line.