The paradox of a cross

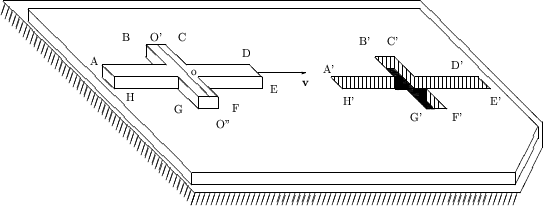
Let a thin plate of large size lie on a solid plane. A small cross is cut out of the plate (Fig. 1.15).

Figure 1.15: The paradox of a cross.

Let the length of this cross be much larger than its cross-beam width $\vert AD\vert \gg \vert BC\vert$. Let the cross slide horizontally over the plate, so that in classical physics it would just occupy its niche and fall into it under the effect of gravity. We choose the relative velocity of motion ${\bf v}$ such that, in accord with relativistic formulas, the length to be shortened two-fold (or even more). Note that the center of gravity of the cross (point $o$) lies also at the cross-beam center. Hence, vertical motions of the cross (falling down, or turning over its front end) is possible only if: 1) center $o$ and the whole central line of a cross-beam ($O'O''$) are over empty space, and 2) none of points $C, D, E, F$ has support. From the viewpoint of an observer on the cross, he will slide over a two-fold shortened niche, since either the cross-beam and one of ends, or both ends of the cross lean against the plate. The known trick with turning of a rod fails in this case (this problem will be considered below). However, from the viewpoint of an observer on the plate, the cross (which became two-fold shorter) will fall down into the niche. Thus, we have two different events: does the downfall of the cross (a push against the plane) take place or not? and what will happen to the observer, who falls down into the niche (will he be crushed or not)? If he escapes, must he promptly begin to move with ${\bf v}$ (as well as the cross), or is he bound to be near the end $A'H'$ (or $D'E'$), because the cross became two-fold shorter? If someone very much wants to re-formulate this paradox as a paradox of existence, that (remembering the remark of the previous paragraph about relativistic "electromagnetic forgeries") a detonator should be under the plate, and a push-button contact could be closed under the plate in the center crosswise niche only with the center of gravity of the cross at its possible falling.