Now, after criticism of the fundamental concept of time for SRT, we continue
the analysis of the logical basis of this theory and consider the
subsidiary
notion of the "relativity of simultaneity". Recall the mental experiment from
SRT: a train
![]() passes along a railroad at speed
passes along a railroad at speed
![]() . Suddenly, lightning
strikes the railroad bed
(
. Suddenly, lightning
strikes the railroad bed
(![]() ) just opposite to the train center
) just opposite to the train center
![]() (at the
moment of coincidence
(at the
moment of coincidence
![]() ). Then, in the coordinate system centered on the
moving train,
the flashes will simultaneously arrive at points
). Then, in the coordinate system centered on the
moving train,
the flashes will simultaneously arrive at points ![]() and
and
![]() ,
whereas for a motionless observer the flashes will simultaneously
arrive at
points
,
whereas for a motionless observer the flashes will simultaneously
arrive at
points ![]() and
and
![]() (with the middle at point
(with the middle at point
![]() ); but up to this instant,
points
); but up to this instant,
points
![]() and
and
![]() (the middles of segments) will move to some distance
from each other.
But a similar situation is possible in classical
physics as well, if we want to transmit information from points
(the middles of segments) will move to some distance
from each other.
But a similar situation is possible in classical
physics as well, if we want to transmit information from points
![]() to the new single point
to the new single point
![]() (or, conversely, to these points
(or, conversely, to these points
![]() from
from
![]() ) at some finite speed
) at some finite speed
![]() (in this case SRT and light
speed constancy will be without
any relevance).
(in this case SRT and light
speed constancy will be without
any relevance).
We can suggest the following mechanical model (Fig. 1.11):
Let four material points (without the force of gravity) fall at speed
One can say that these two events are quite different. But in the case of
the light flash, we have two different events as well. Indeed,
let the light flash occur at the time the centers
Consider now in detail the mental experiment allegedly "demonstrating" the
relativity of simultaneity: at the origins
Recall that the basic positive idea of SRT consisted in the finiteness of the
speed of interactions. The same idea is expressed by a short-range interaction
theory, which reflects the field approach (via the Maxwell equations); namely:
a light wavefront moving from a source to a receiver passes sequentially
through all intermediate points of space. It is just this property that comes
in a conflict with the notion of relativity of simultaneity (Fig. 1.12).
To prove it, we use two statements from the SRT about observers moving
each relative other: 1) one and the same light flash will reach two observers
simultaneously despite the fact that the observers will spatially be separated
by some distance during the light spreading; 2) kinematic formulas of the
SRT (from textbooks) contain squares of velocities only.
For example, let the first observer in system
On the one hand, since the SRT formulas include the square of velocity only,
the second observer will consider the time of signal reception by
the first and third observers to be the same. It can be agreed that
when observers receive the signal under investigation, each of them will send
his signal without delay. If second observer's calculations
are correct, then since the problem is symmetric, he must receive the signals
from the first and third observers simultaneously. On the other hand,
according to Maxwell equations, the light propagates continuously, and
the second observer will receive a signal from the first one simultaneously
with the event, when he himself will see the signal under investigation.
In second observer's opinion, at this time the light has still not reached
the third observer. Thus, the second observer comes
to a contradiction with himself: the first calculations by SRT formulas
contradict the second calculations by the Maxwell equations. Obviously,
the observers will see the flash sequentially, rather than simultaneously,
since the spatial path of light is sequential: the source, the first observer,
then the second and, at last, the third observer.
We additionally note that even within the SRT framework the concept of the
relativity of simultaneity is highly restricted: it is
applicable to two separated events only (there are no intersecting original
causes, no intersecting aftereffects, and, generally, we are not interested
in any additional facts). Indeed, even for these selected points the light
cones have intersections, to say nothing of all other points in space and time.
In fact, we have continuous chains of causally bound (and unbound) events
occurring with multiple intersections through every point of space and time
(not every reason, of course, results in a consequence at a speed of light).
And all this real (different in scale!) time grid is interdependent for the
whole space. Therefore, in the general case we can not change (by choosing
the frame of reference) the order of succession of even causally unbound events
(in any case, this changing would be reflected somewhere).
![]() in pairs over point
in pairs over point ![]() (close to the railroad bed)
and over the train's centre
(close to the railroad bed)
and over the train's centre ![]() which will arrive to the point
which will arrive to the point ![]() near to point
near to point ![]() at the moment of intercept of falling points. Let ideal
reflectors (isosceles triangles with angle at a base
at the moment of intercept of falling points. Let ideal
reflectors (isosceles triangles with angle at a base
![]() )
be installed at point
)
be installed at point
![]() and at train's center.
Then two particles, reflected over
the railroad bed (at point
and at train's center.
Then two particles, reflected over
the railroad bed (at point ![]() ), will
fly to different sides
at speed
), will
fly to different sides
at speed ![]() , and simultaneously reach points
, and simultaneously reach points
![]() and
and
![]() (in the classics
(in the classics
![]() ). This process will
take time
). This process will
take time ![]() , where
, where
![]() is the length of the train. Two other
particles, reflected over the train's center
is the length of the train. Two other
particles, reflected over the train's center ![]() ,
will move after reflection
(relative to the railroad) at speeds
,
will move after reflection
(relative to the railroad) at speeds ![]() (forwards) and
(forwards) and ![]() (backwards). During the same time
(backwards). During the same time
![]() the first of these particles will
traverse the path (forwards)
the first of these particles will
traverse the path (forwards) ![]() , and, since the train
traverses the path
, and, since the train
traverses the path ![]() , the particle will reach
point
, the particle will reach
point ![]() . Similarly, for the second particle
. Similarly, for the second particle
![]() ; hence, it
reaches point
; hence, it
reaches point ![]() . Thus, the event - the falling of points
to the reflectors -
will be recorded at all four points simultaneously: both at points
. Thus, the event - the falling of points
to the reflectors -
will be recorded at all four points simultaneously: both at points
![]() and
and
![]() (over the railroad bed), and at points
(over the railroad bed), and at points
![]() and
and
![]() (over the train).
It is the case when the points, falling over train, participated in its inertial movement. If the second pair of points falls
(over the railroad bed) just over motionless point
(over the train).
It is the case when the points, falling over train, participated in its inertial movement. If the second pair of points falls
(over the railroad bed) just over motionless point ![]() the triangular reflector at the train (only at it) should have the following corners at the basis: against the train movement -
the triangular reflector at the train (only at it) should have the following corners at the basis: against the train movement -
![]() , and in the direction of the train movement -
, and in the direction of the train movement - ![]() . In this case particles will fly in parallel to the train and will reach its ends
simultaneously (but not simultaneously with the second pair of particles!). If we want, that all four material points "have flown by" simultaneously
corresponding points
. In this case particles will fly in parallel to the train and will reach its ends
simultaneously (but not simultaneously with the second pair of particles!). If we want, that all four material points "have flown by" simultaneously
corresponding points ![]() ,
corners at the reflector basis (at the train) should be still reduced by corner
,
corners at the reflector basis (at the train) should be still reduced by corner 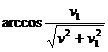 (if to establish a flat waveguide, the pair of particles
over the train will "not rise" too highly, and will move in parallel to the train). Apparently, mechanical analogues are possible for
the most different situations.
(if to establish a flat waveguide, the pair of particles
over the train will "not rise" too highly, and will move in parallel to the train). Apparently, mechanical analogues are possible for
the most different situations.
![]() and
and
![]() of systems
of systems ![]() and
and ![]() moving relative to each other at
moving relative to each other at ![]() coincide. At some time instant
coincide. At some time instant ![]() , the light front will be on the sphere
, the light front will be on the sphere
![]() relative to center
relative to center ![]() in system
in system ![]() and on the sphere
and on the sphere ![]() with
center
with
center ![]() in system
in system ![]() (which seems to be impossible). However, there is
nothing surprising (i.e. contradicting classical physics) in this
situation, because the observers in system
(which seems to be impossible). However, there is
nothing surprising (i.e. contradicting classical physics) in this
situation, because the observers in system ![]() and
and ![]() will record the
same light to have different frequencies
will record the
same light to have different frequencies ![]() and
and ![]() by virtue
of the Doppler effect. But in this case these are two identifiably
different events: the observers can always compare the results of
measurements
by virtue
of the Doppler effect. But in this case these are two identifiably
different events: the observers can always compare the results of
measurements ![]() and
and ![]() upon meeting!
upon meeting!
![]() and
and ![]() of reference systems
of reference systems ![]() and
and ![]() that move relative to each other, a light flash occurs at the time of
their coincidence. According to SRT, during the time
that move relative to each other, a light flash occurs at the time of
their coincidence. According to SRT, during the time
![]() on the clock of system
on the clock of system ![]() , the light will pass
the distance
, the light will pass
the distance ![]() from center
from center ![]() . For the same time
. For the same time
![]() on the clock of system
on the clock of system ![]() , the same light will
pass the distance
, the same light will
pass the distance ![]() from center
from center ![]() . The time difference
. The time difference
![]() is not influenced by any adjustment of initial times,
whether accomplished before the experiment, or after it by any method.
For example, an infinitely remote periodic source located perpendicular
to the direction of motion can be used. It is possible to
agree in advance about the flashes, recorded on the clock of system
is not influenced by any adjustment of initial times,
whether accomplished before the experiment, or after it by any method.
For example, an infinitely remote periodic source located perpendicular
to the direction of motion can be used. It is possible to
agree in advance about the flashes, recorded on the clock of system ![]() (for example, periodically each million years), and "to organize" system
(for example, periodically each million years), and "to organize" system ![]() for one instant before the flash occurs, selected in advance (the paradox of
non-locality, associated with this, will be considered in Section 1.7).
for one instant before the flash occurs, selected in advance (the paradox of
non-locality, associated with this, will be considered in Section 1.7).
![]() be moving towards the flash
source at slow speed
be moving towards the flash
source at slow speed ![]() m/s. Since the distance to the flash point is
large (say a million light years), then for one million years both observers
will separate from each other to a large distance - about
m/s. Since the distance to the flash point is
large (say a million light years), then for one million years both observers
will separate from each other to a large distance - about
![]() m. According to SRT formulas, the times of arrival
of a signal will be the same for both observers. At what point of space
did the first observer "pass" the light wavefront for the second observer?
But what if he had held a mirror for the whole million years, and removed it
one second before receiving a signal? In the second observer's opinion,
the signal was reflected by the first observer somewhere ahead. But
in this case what thing was reflected by the first observer, if none of his
instruments did still respond to a flash? Similarly, a third observer
can go away from the second one at the same velocity, but directed from
the source. If the second observer held a mirror for a million of years except
one second, would the third one see the light?
m. According to SRT formulas, the times of arrival
of a signal will be the same for both observers. At what point of space
did the first observer "pass" the light wavefront for the second observer?
But what if he had held a mirror for the whole million years, and removed it
one second before receiving a signal? In the second observer's opinion,
the signal was reflected by the first observer somewhere ahead. But
in this case what thing was reflected by the first observer, if none of his
instruments did still respond to a flash? Similarly, a third observer
can go away from the second one at the same velocity, but directed from
the source. If the second observer held a mirror for a million of years except
one second, would the third one see the light?
![]()
![]()
![]()
![]()
Next: The Lorentz transformations
Up: Kinematics of special relativity
Previous: Additional remarks
Contents
Sergey N. Arteha